Aufgaben zu Wachstums- und Zerfallsprozessen

Bei einem radioaktiven Stoff zerfällt jedes Jahr 10% der noch vorhandenen Masse. Berechne, wie viel nach 10 Jahren noch vorhanden ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum

Wenn jedes Jahr 10% zerfallen, dann sind im Umkehrschluss nach jedem Jahr noch 90% vom Vorjahr vorhanden. Wir bezeichnen die Masse des Stoffes im Jahr 0 mit $m_0$ , im Jahr 1 mit $m_1$ , im Jahr 2 mit $m_2$ …, im Jahr 10 mit $m_{10}$ .

Jahr	noch vorhandene Masse
0	$m_0$
1	$m_1=0{,}9 \cdot m_0$
2	$m_2=0{,}9 \cdot m_1=0{,}9 \cdot 0{,}9 \cdot m_0 = (0{,}9)^2\cdot m_0$
3	$m_3=0{,}9 \cdot m_2=0{,}9 \cdot 0{,}9 \cdot 0{,}9 \cdot m_0 = (0{,}9)^3\cdot m_0$
$\vdots$	$\vdots$
9	$m_9=0{,}9 \cdot m_8=0{,}9\cdot (0{,}9^8 \cdot m_0)=0{,}9^9m_0$
10	$m_{10}=0{,}9 \cdot m_9=0{,}9\cdot (0{,}9^9 \cdot m_0)=0{,}9^{10} \cdot m_0$

$m_{10}=0{,}9 \cdot m_9=0{,}9^{10} \cdot m_0$ $\approx 0{,}3487 \cdot m_0$

Nach 10 Jahren sind also etwa 34,87% des ursprünglichen Materials vorhanden.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Modelliere jeweils durch einen entsprechenden Funktionsterm $\mathrm f(\mathrm x)$ :

Die Tabelle zeigt die Entwicklung des ökologischen Landbaus in Deutschland:

Jahr	1984	1990	1996	2002
Fläche in 1000 ha	22	84	313	632

Falls die Entwicklung von 1990 bis 1996 durch eine Exponentialfunktion der Bauart $f(x)=84\, a^ x$ beschrieben wird, wie lautet dann die Basis $a$ und wie ist dieser Wert zu interpretieren?

Überprüfe, ob die Daten von 1984 und 2002 zu dieser Modellierung passen.

Wann (in der Vergangenheit) startete nach diesem Modell die Fläche bei 0 ha?

Von einem radioaktiven Element sind anfangs 20 000 Atomkerne vorhanden, nach 183 Sekunden ist nur noch $\frac{1}{10}$ davon vorhanden.

Wann ist nur die Hälfte vorhanden (Halbwertszeit)?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zerfallsprozesse

Verwende die allgemeine Formel für Zerfallsprozesse.

Um die Halbwertszeit bestimmen zu können, benötigst du zunächst die Zerfallskonstante $\lambda$ .

\displaystyle N(t)=N_0\cdot e^{-\lambda\cdot t}

Setze die aus der Aufgabenstellung bekannten Zahlen in die Formel ein. Dadurch erhältst du eine Gleichung in Abhängigkeit von $\lambda$ .

$\displaystyle N(183\,\mathrm{s})$	$=$	$\displaystyle \frac{1}{10} \cdot N_0$
$\displaystyle N_0 \cdot e^{-\lambda \cdot 183\,\mathrm{s}}$	$=$	$\displaystyle \frac{1}{10}N_0$	$\displaystyle :N_0$
$\displaystyle e^{-\lambda \cdot 183\,\mathrm{s}}$	$=$	$\displaystyle \frac{1}{10}$	$\displaystyle \ln$
	↓	Wende die Umkehrfunktion der $e$ -Funktion an.
$\displaystyle -\lambda \cdot 183\,\mathrm{s}$	$=$	$\displaystyle \ln\left(\frac{1}{10}\right)$
	↓	Verwende zur Vereinfachung die Rechenregeln des Logarithmus: $\ln \left(\frac{1}{10}\right)=\ln (10^{-1})=-\ln (10)$
$\displaystyle -\lambda \cdot 183\,\mathrm{s}$	$=$	$\displaystyle -\ln(10)$	$\displaystyle \cdot\left(-1\right)$
$\displaystyle \lambda \cdot 183\,\mathrm{s}$	$=$	$\displaystyle \ln(10)$	$\displaystyle :183$
$\displaystyle \lambda$	$=$	$\displaystyle \frac{\ln(10)}{183\,\mathrm{s}}$

Jetzt kennst du die Zerfallskonstante. Bestimme nun die gesuchte Halbwertszeit $T$ .

Hierzu verwende die Definition der Halbwertszeit: nach der Halbwertszeit $T$ sind noch die Hälfte der Teilchen vorhanden.

$\displaystyle N\left(T\right)$	$=$	$\displaystyle \frac{N_0}{2}$
$\displaystyle N_0\cdot e^{-\lambda T}$	$=$	$\displaystyle \frac{N_0}{2}$	$\displaystyle :N_0$
$\displaystyle e^{-\lambda T}$	$=$	$\displaystyle \frac{1}{2}$	$\displaystyle \ln$
	↓	Wende die Umkehrfunktion der $e$ -Funktion an.
$\displaystyle -\lambda T$	$=$	$\displaystyle \ln\left(\frac{1}{2}\right)$
	↓	$\ln(\frac{1}{2})=\ln(1)-\ln(2)=-\ln(2)$
$\displaystyle -\lambda T$	$=$	$\displaystyle -\ln(2)$	$\displaystyle :(-\lambda)$
$\displaystyle T$	$=$	$\displaystyle \frac{\ln\left(2\right)}{\lambda}$
	↓	Setze $\lambda$ ein.
$\displaystyle T$	$=$	$\displaystyle \ln(2) \cdot \left(\frac{183\,\mathrm{s}}{\ln(10)}\right)$
$\displaystyle T$	$≈$	$\displaystyle 55{,}088\,\mathrm{s}$

Die Halbwertzeit beträgt rund $55{,}1\;\mathrm{ s}$ .

Lösung mithilfe der allgemeinen Potenzfunktion

Gegenstand der Aufgabe ist es, die Halbwertszeit des vorliegenden radioaktiven Elements zu ermitteln. Dazu benötigst du in dieser Lösungsvariante die allgemeine Potenzfunktion, deren Gleichung $N(t)=b\cdot a^t$ lautet.

Ausgangssituation:

Anfangs ( $t=0$ ) sind $N(0)=20000$ Kerne vorhanden

$\displaystyle N(0)$	$=$	$\displaystyle b\cdot a^0$
$\displaystyle 20000$	$=$	$\displaystyle b\cdot a^0$
	↓	Da $a^0=1$ , ist nun der Wert des Parameters $b$ bekannt.
$\displaystyle b$	$=$	$\displaystyle 20000$

Situation nach 183 Sekunden:

Nach 183 Sekunden existieren noch $\frac{1}{10}$ der anfangs vorhanden Kerne.

Also: $N(183)=\frac{1}{10}\cdot N(0)$

$\displaystyle N(183)$	$=$	$\displaystyle 20000\cdot a^{183}$
$\displaystyle \frac{1}{10}\cdot N(0)$	$=$	$\displaystyle 20000\cdot a^{183}$
	↓	Setze $N(0 )=20000$ ein
$\displaystyle 2000$	$=$	$\displaystyle 20000\cdot a^{183}$	$\displaystyle :20000$
$\displaystyle 0{,}1$	$=$	$\displaystyle a^{183}$	$\displaystyle \sqrt[183]{}$
$\displaystyle a$	$=$	$\displaystyle \sqrt[183]{0{,}1}$
	$≈$	$\displaystyle 0{,}9875$

Resultierender Funktionsterm

Nachdem du die Werte der beiden Parameter bestimmt hast, kennst du nun den Funktionsterm, der die Anzahl der noch vorhandenen Kerne in Abhängigkeit von der verstrichenen Zeit beschreibt.

\displaystyle N(t)=N_0\cdot e^{-\lambda\cdot t}

Bestimmung der Halbwertszeit

Du suchst nun die Zeit T, zu der die Anzahl noch der vorhandenen Kerne genau halb so groß ist wie jene zu Beginn. Es gilt also:

\displaystyle N(t)=N_0\cdot e^{-\lambda\cdot t}

Verwende den zuvor ermittelten Funktionsterm $N(t)$

$\displaystyle N(T)$	$=$	$\displaystyle \frac{1}{2}\cdot N(0)$
$\displaystyle 20000\cdot 0{,}9875^T$	$=$	$\displaystyle \frac{1}{2} \cdot 20000\cdot 0{,}9875^0$
$\displaystyle 0{,}9875^T$	$=$	$\displaystyle \frac{1}{2}\cdot0{,}9875^0$
$\displaystyle 0{,}9875^T$	$=$	$\displaystyle \frac{1}{2}$	$\displaystyle \ln()$
$\displaystyle T\cdot \ln(0{,}9875)$	$=$	$\displaystyle \ln(\frac{1}{2})$	$\displaystyle :\ln(0{,}9875)$
$\displaystyle T$	$=$	$\displaystyle \dfrac{\ln(\frac{1}{2})}{\ln(0{,}9875)}$
$\displaystyle T$	$≈$	$\displaystyle 55{,}1$

Ergebnis: Die Halbwertszeit T beträgt etwa 55,1 Sekunden.

Bemerkung

Das in dieser Variante ermittelte Ergebnis weicht geringfügig von dem der alternativen Aufgabenlösung (siehe oben) ab, weil du mit dem gerundeten Wert $0{,}9875$ für den Parameter $a$ weitergerechnet hast. Bei Verwendung des ungerundeten Zwischenergebnisses $a=\sqrt[183]{0{,}1}$ erhältst du analog zum obigen Lösungsvorschlag eine Halbwertszeit von $T=\frac{\ln{(\frac{1}{2})}}{\ln{\left(\sqrt[183]{0{,}1}\right)}}=55{,}088$ Sekunden.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Ein Hersteller von Bleistiften hat anfangs 20 000 Stifte in seinem Lager,
nach 183 Tagen ist (bei gleichmäßiger Nachfrage seitens der Kunden) nur noch $\frac{1}{10}$ davon vorrätig, wenn währenddessen keine Stifte produziert werden.
Ergibt sich eine lineare oder exponentielle Abnahme für $f(x)=$ Vorrat nach $x$ Tagen?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wachstumsprozesse - eine Übersicht
Lineare oder exponentielle Abnahme für $f(x)=$ Vorrat nach $x$ Tagen?
Es handelt sich um eine lineare Abnahme, weil von einer gleichmäßigen Nachfrage gesprochen wird. Das heißt, die Kunden kaufen jeden Tag die gleiche Menge an Stifte.
Exponentiell wäre der Zusammenhang genau dann, wenn die Nachfrage der Kunden gleichmäßig bspw. um $10~\%$ jeden Tag ansteigen würde.
Es sind noch $\dfrac{1}{10}$ von $20000$ gleich $2000$ Bleistifte vorrätig, d.h. es wurden $18000$ Stifte verkauft.
Pro Tag nahm der Vorrat um $\dfrac{18000}{183}\approx98$ Stifte ab.
Die lineare Funktionsgleichung lautet demnach:
.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne, wie viele Stifte verkauft wurden.
Berechne den Verkauf pro Tag.

3
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
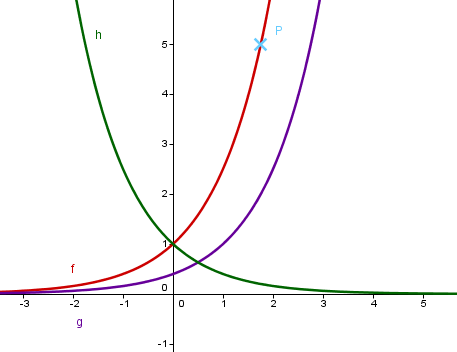
Zeichne mit Hilfe einer Wertetabelle die Graphen zu $\mathrm f(\mathrm x)=2{,}5^\mathrm x$ , $\mathrm g(\mathrm x)=2{,}5^{\mathrm x-1}$ und $\mathrm h(\mathrm x)=0{,}4^\mathrm x$ .
Vergleiche die Graphen.
Löse die Gleichung $2{,}5^\mathrm x=5$ graphisch.

Für diese Aufgabe benötigst Du folgendes Grundwissen: exponentielles Wachstum
Wertetabelle anlegen
$x$
-3
-2
-1
0
1
2
3
4
$f(x)$
0,064
0,16
0,4
1
2,5
6,25
15,625
39,0625
$g(x)$
0,0256
0,064
0,16
0,4
1
2,5
6,25
15,625
$h(x)$
15,625
6,25
2,5
1
0,4
0,16
0,064
0,0256
Graphen zeichnen

Graphen vergleichen
g ist im Vergleich zu f um 1 nach rechts verschoben
h ist im Vergleich zu f an der y-Achse gespiegelt

Lösung der Gleichung ablesen
$P=\left(1{,}76\;\left|5\right.\right)$
4
Derzeit gibt es kein politisches System auf der Erde, das nicht auf Wirtschaftswachstum setzt. $4\ \%$ Wachstum gelten als wünschenswert und maßvoll: also jedes Jahr $4\ \%$ mehr im Vergleich zum Vorjahr. Um wie viel Prozent wäre also bei diesem Wachstum die Wirtschaft nach…
1. … 2 Jahren gewachsen?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
  $4\%$ -iges Wachstum bedeutet, dass die Wirtschaftskraft das $1{,}04$ fache vom Vorjahr beträgt.
  Nach 2 Jahren also das $1{,}04\cdot 1{,}04=1{,}0816$ fache vom Ausgangsjahr. Das entspricht einem Zuwachs von $8{,}16\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. … 10 Jahren gewachsen?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
  $1{,}04^{10}=1{,}48024.$ Sie wäre also rund um das $1{,}5$ -fache gewachsen. Der Zuwachs wäre $48\%$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. … 50 Jahren gewachsen?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
  Lösung: $1{,}04^{50}=7{,}10668$
  Nach 50 Jahren müsste sich die Wirtschaftsleistung etwa versiebenfacht haben. Fragt sich nur, wo da die Resourcen herkommen sollen…
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

$x$	-3	-2	-1	0	1	2	3	4
$f(x)$	0,064	0,16	0,4	1	2,5	6,25	15,625	39,0625
$g(x)$	0,0256	0,064	0,16	0,4	1	2,5	6,25	15,625
$h(x)$	15,625	6,25	2,5	1	0,4	0,16	0,064	0,0256

Hans eröffnet am 1. Januar ein Konto und zahlt darauf $500\ €$ ein.

Er erhält jährlich $2{,}5\ \%$ Zinsen, die er am Ende des Jahres jeweils auf das Konto gutschreiben lässt

Wie lautet der Kontostand nach 1, 2, 5 bzw. 10 Jahren?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
Allgemeine Formel für exponentielles Wachstum:
Wachstumsfaktor: $b\ =\ 1{,}025$
Anfangswert: $a = 500\;$
Exponent: $\left[t\right]$ in Jahren
$\left[y\right]$ in Euro
Erhält Hans jährlich $2{,}5\%$ Zinsen auf sein Kapital so beträgt sein Kontostand das $1{,}025$ -fache des vorherigen Betrags von $500$ Euro.
Gesucht ist jeweils $y$ , wenn die Werte $1, 2, 5$ und $10$ für $t$ eingesetzt werden
Exponent = $\left[t\right]$ in Jahren = $1$
Nach einem Jahr ist sein Kontostand um das genau $1{,}025^1$ -fache des vorherigen Betrages gestiegen.
$500\cdot1{,}025^1=512{,}50 \;\text{Euro}$
Exponent = $\left[t\right]$ in Jahren = $2$
Nach zwei Jahren wird auf den vorherigen bezinsten Betrag erneut das $1{,}025$ fache aufgeschlagen. Ein Zuwachs von $1{,}025\cdot1{,}025\;$ also $5{,}1\%$ .
$500\cdot1{,}025^2=525{,}31 \;\text{Euro}$
Exponent = $\left[t\right]$ in Jahren = 5
$500\cdot1{,}025^5=565{,}70 \; \text{Euro}$
Exponent= $\left[t\right]$ in Jahren = 10
$500\cdot1{,}025^{10}=640{,}04\; \text{Euro}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Wie lange müsste Hans warten, damit sich sein Anfangskapital von $500\ €$ verdoppelt hat?

Bakterien vermehren sich durch Teilung, wobei sich eine Bakterienzelle durchschnittlich alle 10 Minuten teilt. Zum Zeitpunkt $t=0$ sei genau eine Bakterienzelle vorhanden.

Wie viele Bakterien sind dann nach 1 Stunde, 2 Stunden, 6 Stunden, 12 Stunden bzw. 24 Stunden vorhanden?

Finde eine Formel für die Anzahl $N= N(t)$ der Bakterien nach der Zeit $t$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: exponentielles Wachstum
$1\cdot 1{,}072^t=N\left(t\right)$
Siehe 1. Teilaufgabe.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Eine Bakterienzelle hat ein Volumen von ca. $2 \cdot 10^{-18}\;\mathrm m^3$ . Wie lange dauert es, bis die Bakterienkultur ein Volumen von $1\ m^3$ bzw. $1\ km^3$ einnimmt? Beurteile dein Ergebnis kritisch.

Für diese Aufgabe benötigst Du folgendes Grundwissen: exponentielles Wachstum
1. Volumen
Formel:
$2\cdot10^{-18}\,m^3\cdot1{,}072^t=1\,m^3$
$1{,}072^t$ entspricht der Anzahl der Bakterien nach einer bestimmten Zeit. Das Produkt dieser Anzahl und dem Volumen einer einzelnen Bakterie wird mit dem gesuchten Volumen $1m^3$ gleichgesetzt.
$1{,}072^t=5\cdot 10^{17}$
Logarithmiere.
$\log _{1{,}072}\left(5\cdot 10^{17}\right)\approx 586{,}16$
Rechne $586{,}16$ Minuten in Stunden um.
⇒ Es dauert ca. 9,77 Stunden bis die Bakterienkultur ein Volumen von $1m^3$ erreicht hat.
2. Volumen
$2\cdot10^{-18}\,m^3\cdot1{,}072^t=1000000000\,m^3$
$1{,}072^t$ entspricht der Anzahl der Bakterien nach einer bestimmten Zeit. Das Produkt dieser Anzahl und dem Volumen einer einzelnen Bakterie wird mit dem gesuchten Volumen $1000000000\,m^3$ gleichgesetzt.
$1{,}072^t=5\cdot 10^{26}$
Logarithmiere.
$\log _{1{,}072}\left(5\cdot 10^{26}\right)=884{,}22$
⇒ Es dauert ca. 14,74 Stunden bis die Bakterienkultur ein Volumen von $1000000000\,m^3$ erreicht hat.
Vor allem letzteres Ergebnis ist kritisch zu betrachten, da das Labor selbst kaum ein Volumen von $1 \, km^3$ hat, sondern viel kleiner ist. Selbst wenn man merken würde, dass eine Bakterienkultur auf $1 \, m^3$ anwächst, würde man dagegen etwas unternehmen! Trotzdem ist es interessant zu sehen, dass es theoretisch nur etwa $13$ Stunden dauern würde, bis sich Bakterien derart vermehren.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Ein Taucher interessiert sich wegen Unterwasseraufnahmen dafür, welche Helligkeit in verschiedenen Tiefen herrscht.

Messungen in einem bestimmten (recht trüben) See ergeben, dass die Helligkeit pro Meter Wassertiefe um ca. 17% abnimmt.

Für diese Aufgabe musst du dich mit exponentiellem Wachstum auskennen

allg. Formel $H_0\cdot b^x=H$

Abnahmefaktor $b=0{,}83$

Anfangswert $H_0=1$ $\left(=100\%\right)$

Exponent= $\left[x\right]$ in Metern

$\left[H\right]$ in Prozent

Wie groß ist die Helligkeit in 1m, 2m, 5m bzw. 10m Tiefe, verglichen mit der Helligkeit an der Wasseroberfläche?

Für diese Aufgabe benötigst Du folgendes Grundwissen: exponentielles Wachstum
$x=1\ \text{m}$
$100\%\cdot0{,}83=83\%$ der Helligkeit an der Wasseroberfläche ist noch vorhanden.
$x=2\ \text{m}$
$83\%\cdot0{,}83\cdot0{,}83=68{,}89\%$ der Helligkeit an der Wasseroberfläche ist noch vorhanden.
$x=5\ \text{m}$
$68{,}89\%\cdot0{,}83\cdot0{,}83\cdot0{,}83=39{,}39\%$ der Helligkeit an der Wasseroberfläche ist noch vorhanden.
$x=10\ \text{m}$
$39{,}39\%\cdot0{,}83^5=15{,}52\%$ der Helligkeit an der Wasseroberfläche ist noch vorhanden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Beschreiben sie die Helligkeit H als Funktion der Wassertiefe x als Bruchteil der Helligkeit ${\mathrm H}_0$ an der Wasseroberfläche.

Für diese Aufgabe benötigst Du folgendes Grundwissen: exponentielles Wachstum
Formel: $H_0\cdot0{,}83^x=H$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

In welcher Tiefe beträgt die Helligkeit weniger als $0{,}01\cdot{\mathrm H}_0$ ?

Beim Reaktorunglück von Tschernobyl wurde eine Menge von etwa $400\ g$ radioaktiven Jod 131 freigesetzt.

Dieses Jod 131 hat eine sogenannte Halbwertszeit von 8,0 Tagen, d.h. in jeweils 8,0 Tagen halbiert sich die Menge des noch vorhandenen radioaktiven Materials Jod 131.

Allg. Formel: $M\left(0\right)\cdot b^t=M\left(t\right)$

Anfangswert a = $400g$ $=M\left(0\right)$

Zeit $\left[t\right]$ in Tagen

$M\left(t\right)\;in\;g$

$M\left(8\right)=200g$

Wie kann man die Menge $\mathrm M=\mathrm M\left(\mathrm t\right)$ des radioaktiven Jods 131 als Funktion der Zeit $t$ angeben?

Welcher Prozentsatz der ursprünglich vorhandenen Menge ${\mathrm M}_0=400\mathrm g$ war nach einem Tag bzw. nach 30 Tagen noch vorhanden?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
$M\left(1\right)=400g\cdot 0{,}917^1 = 366{,}8g$
Das entspricht einem Anteil der ursprünglichen Menge von:
$\frac{366{,}8}{400}=0{,}917=91{,}7\%$
$M\left(30\right)=400g\cdot0{,}917^{30} \approx29{,}73$
Das entspricht einem Anteil der ursprünglichen Menge von:
$\frac{29{,}73}{400}\approx0{,}074=7{,}4\%$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Wie lange musste man etwa warten, bis von den 400g Jod 131 nur noch 1 Milligramm vorhanden war?

Bierschaumzerfall

Bei einer schlecht eingeschenkten Maß Bier beträgt die Schaumhöhe anfangs $10\ cm$ . Um das Bier einigermaßen trinken zu können, wartet der Gast eine gewisse Zeit. Nach 3 Minuten ist die Schaumhöhe auf die Hälfte zurückgegangen.

Stelle die Zerfallsgleichung für den Bierschaumzerfall auf.

Berechne, wann die Schaumhöhe auf $1\ cm$ zurückgegangen ist.

Bei einem anderen Gast beträgt die Schaumhöhe nach drei Minuten noch $3\ cm$ . Wie war die Schaumhöhe nach dem Einschenken?

Mache plausibel, wann der Zerfall am stärksten ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
Die Zerfallsfunktion ist eine Exponentialfunktion mit einer Basis, die kleiner $1$ ist.
Am Graphen erkennst du, dass der Zerfall am Anfang am stärksten ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle f(6)$	$=$	$\displaystyle 84\cdot a^6$
$\displaystyle 313$	$=$	$\displaystyle 84\cdot a^6$
$\displaystyle \Rightarrow\;a^6$	$=$	$\displaystyle \dfrac{313}{84}$	$\displaystyle \sqrt[6]{~}$
$\displaystyle a$	$=$	$\displaystyle \sqrt[6]{\dfrac{313}{84}}$
	$≈$	$\displaystyle 1{,}245$

$\displaystyle 500\cdot1{,}025^t$	$=$	$\displaystyle 1000$	$\displaystyle :\ 500$
$\displaystyle 1{,}025^t$	$=$	$\displaystyle 2$	$\displaystyle \cdot\log\left(\right)$
	↓	Logarithmiere.
$\displaystyle \log_{1{,}025}\left(2\right)$	$=$	$\displaystyle t$
$\displaystyle t$	$≈$	$\displaystyle 28{,}1\;\text{Jahre}$

$\displaystyle 0{,}01 \cdot H_0$	$=$	$\displaystyle H$
$\displaystyle 0{,}01 \cdot H_0$	$=$	$\displaystyle H_0 \cdot 0{,}83^x$	$\displaystyle \colon H_0$
	↓	Kürze $H_0$ heraus.
$\displaystyle 0{,}01$	$=$	$\displaystyle 0{,}83^x$	$\displaystyle \log_{0{,}83}()$
	↓	Logarithmiere.
$\displaystyle \log_{0{,}83}\left(0{,}01\right)$	$=$	$\displaystyle x$
$\displaystyle 24{,}72\ \text{m}$	$=$	$\displaystyle x$

$\displaystyle 400g\ \cdot b^8$	$=$	$\displaystyle 200g$	$\displaystyle \colon 400g$
$\displaystyle b^8$	$=$	$\displaystyle \frac12$	$\displaystyle \sqrt[8]{}$
$\displaystyle b$	$=$	$\displaystyle \sqrt[8]{\frac12}$
$\displaystyle b$	$≈$	$\displaystyle 0{,}917$

$\displaystyle \frac{1}{1000}g$	$=$	$\displaystyle 400 g \cdot 0{,}917^t$	$\displaystyle \colon 400 g$
$\displaystyle \frac{1}{400000} g$	$=$	$\displaystyle 0{,}917^t$	$\displaystyle \log_{0{,}917}$
	↓	Logarithmiere.
$\displaystyle \log _{0{,}917}\left(\frac{1}{400000}\right)$	$=$	$\displaystyle t$
$\displaystyle 148{,}87$	$=$	$\displaystyle t$

$\displaystyle 1\cdot b^{10}$	$=$	$\displaystyle 2$	$\displaystyle \sqrt[10]{}$
	↓	Ziehe die Wurzel.
$\displaystyle \sqrt[10]{2}$	$=$	$\displaystyle b$
$\displaystyle 1{,}072$	$≈$	$\displaystyle b$

$\displaystyle 0{,}5\cdot10$	$=$	$\displaystyle 10\cdot(1-p)^3$	$\displaystyle \colon 10$
$\displaystyle 0{,}5$	$=$	$\displaystyle (1-p)^3$	$\displaystyle \sqrt[3]{}$
$\displaystyle \sqrt[3]{\frac{1}{2}}$	$=$	$\displaystyle 1-p$	$\displaystyle +p-\sqrt[3]{\frac{1}{2}}$
$\displaystyle p$	$=$	$\displaystyle 1-\sqrt[3]{\frac{1}{2}}$

$\displaystyle 1$	$=$	$\displaystyle 10\left(\sqrt[3]{\frac{1}{2}}\right)^t$	$\displaystyle \colon 10$
$\displaystyle 0{,}1$	$=$	$\displaystyle \left(\sqrt[3]{\frac{1}{2}}\right)^t$	$\displaystyle \log_{\left(\sqrt[3]{\tfrac{1}{2}}\right)}$
$\displaystyle \log_{\left(\sqrt[3]{\tfrac12}\right)}{0{,}1}$	$=$	$\displaystyle t$
$\displaystyle 10$	$≈$	$\displaystyle t$

$\displaystyle f_0\left(\sqrt[3]{\frac{1}{2}}\right)^3$	$=$	$\displaystyle 3$
$\displaystyle f_0\cdot \frac{1}{2}$	$=$	$\displaystyle 3$	$\displaystyle \cdot 2$
$\displaystyle f_0$	$=$	$\displaystyle 6$

Aufgaben zu Wachstums- und Zerfallsprozessen

Entwicklung von 1990 bis 1996 durch eine Exponentialfunktion f(x)=84 axf(x)=84\, a^ xf(x)=84ax

Wie ist dieser Wert für a zu interpretieren?

Passen die Daten von 1984 und 2002 zu dieser Modellierung

Wann (in der Vergangenheit) startete nach diesem Modell die Fläche bei 0 ha?

Hast du eine Frage oder Feedback?

Lösung mithilfe der allgemeinen Potenzfunktion

Ausgangssituation:

Situation nach 183 Sekunden:

Resultierender Funktionsterm

Bestimmung der Halbwertszeit

Ergebnis: Die Halbwertszeit T beträgt etwa 55,1 Sekunden.

Bemerkung

Hast du eine Frage oder Feedback?

Lineare oder exponentielle Abnahme für f(x)=f(x)=f(x)= Vorrat nach xxx Tagen?

Hast du eine Frage oder Feedback?

Wertetabelle anlegen

Graphen zeichnen

Graphen vergleichen

Lösung der Gleichung ablesen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Exponent = [t]\left[t\right][t] in Jahren = 111

Exponent = [t]\left[t\right][t] in Jahren = 222

Exponent = [t]\left[t\right][t] in Jahren = 5

Exponent= [t]\left[t\right][t] in Jahren = 10

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Gesucht ist der Wachstumsfaktor b

Die Formel für die Bakterien nach einer bestimmten Zeit t ist also gegeben durch:

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

1. Volumen

2. Volumen

2⋅10−18 m3⋅1,072t=1000000000 m32\cdot10^{-18}\,m^3\cdot1{,}072^t=1000000000\,m^32⋅10−18m3⋅1,072t=1000000000m3

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Gesucht ist der Abnahmefaktor b

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Entwicklung von 1990 bis 1996 durch eine Exponentialfunktion $f(x)=84\, a^ x$

Lineare oder exponentielle Abnahme für $f(x)=$ Vorrat nach $x$ Tagen?

Exponent = $\left[t\right]$ in Jahren = $1$

Exponent = $\left[t\right]$ in Jahren = $2$

Exponent = $\left[t\right]$ in Jahren = 5

Exponent= $\left[t\right]$ in Jahren = 10

$2\cdot10^{-18}\,m^3\cdot1{,}072^t=1000000000\,m^3$