Graphisches Differenzieren einer linearen Funktion
Die lineare Funktion soll graphisch differenziert werden.
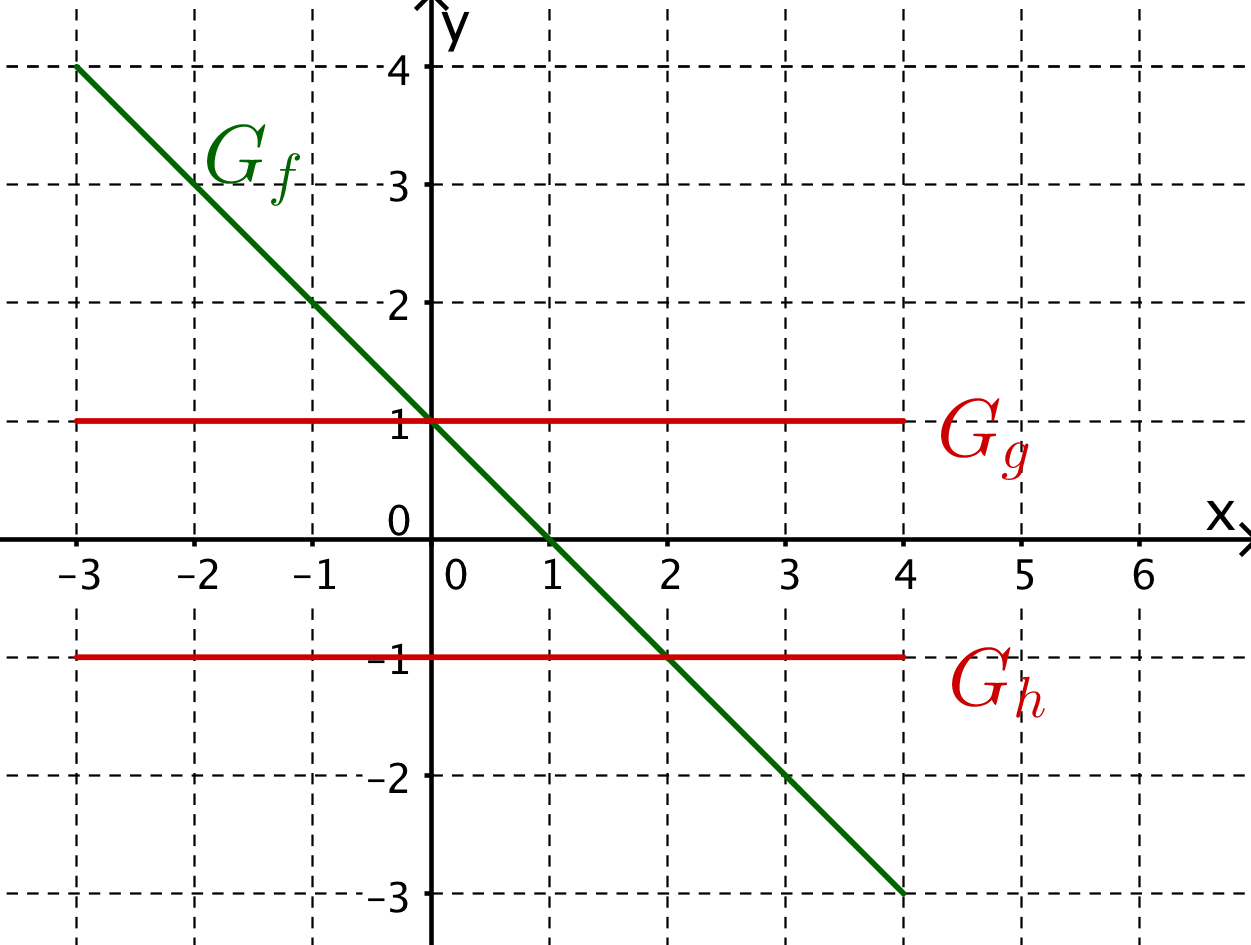
Betrachte die gegebenen Graphen und entscheide, was zutrifft.
Graphisches Differenzieren einer ganzrationalen Funktion 2. Grades
Die quadratische Funktion p soll graphisch differenziert werden.
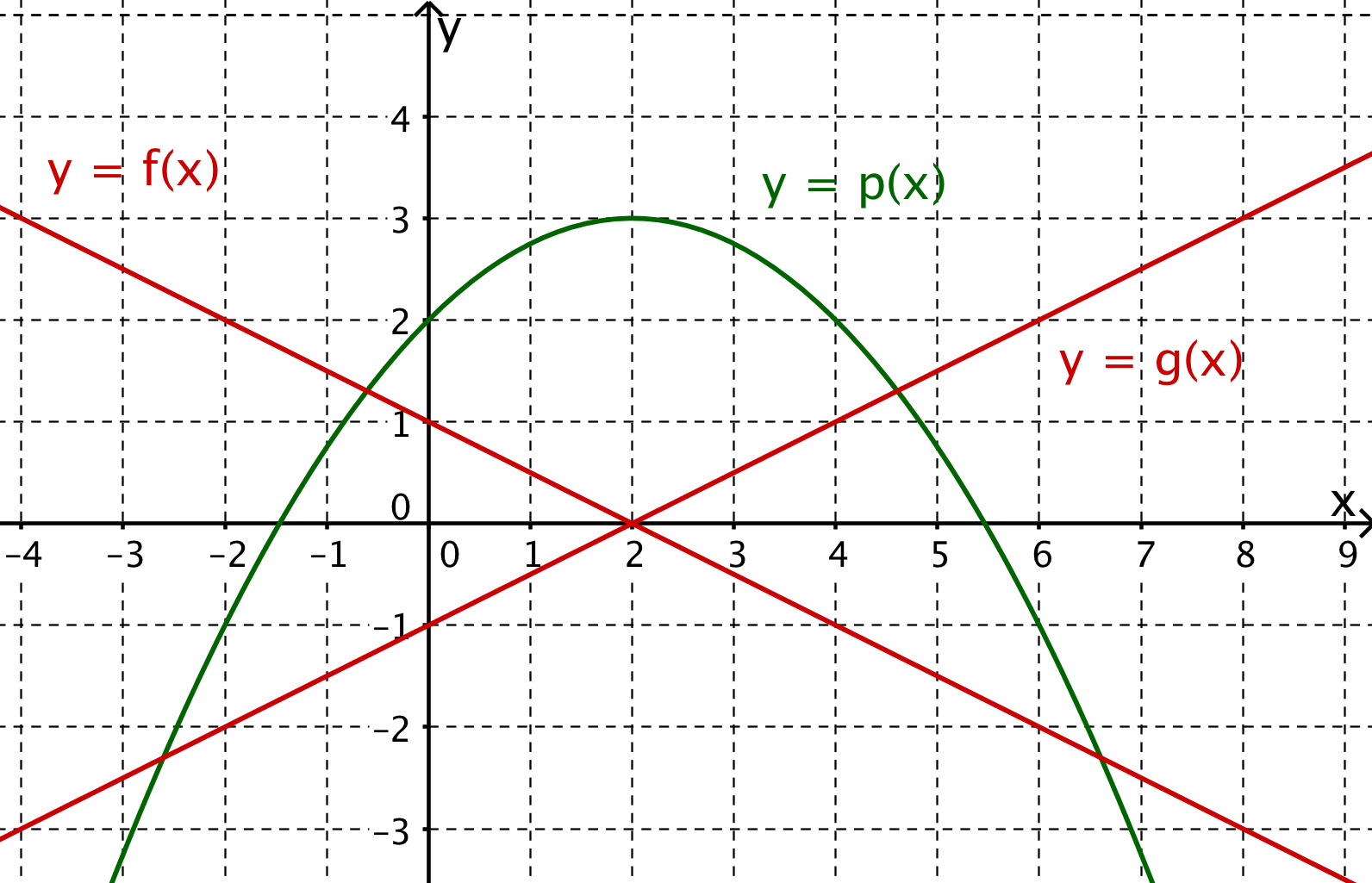
Entscheide, welche der beiden Funktionen oder die Ableitungsfunktion von p ist.
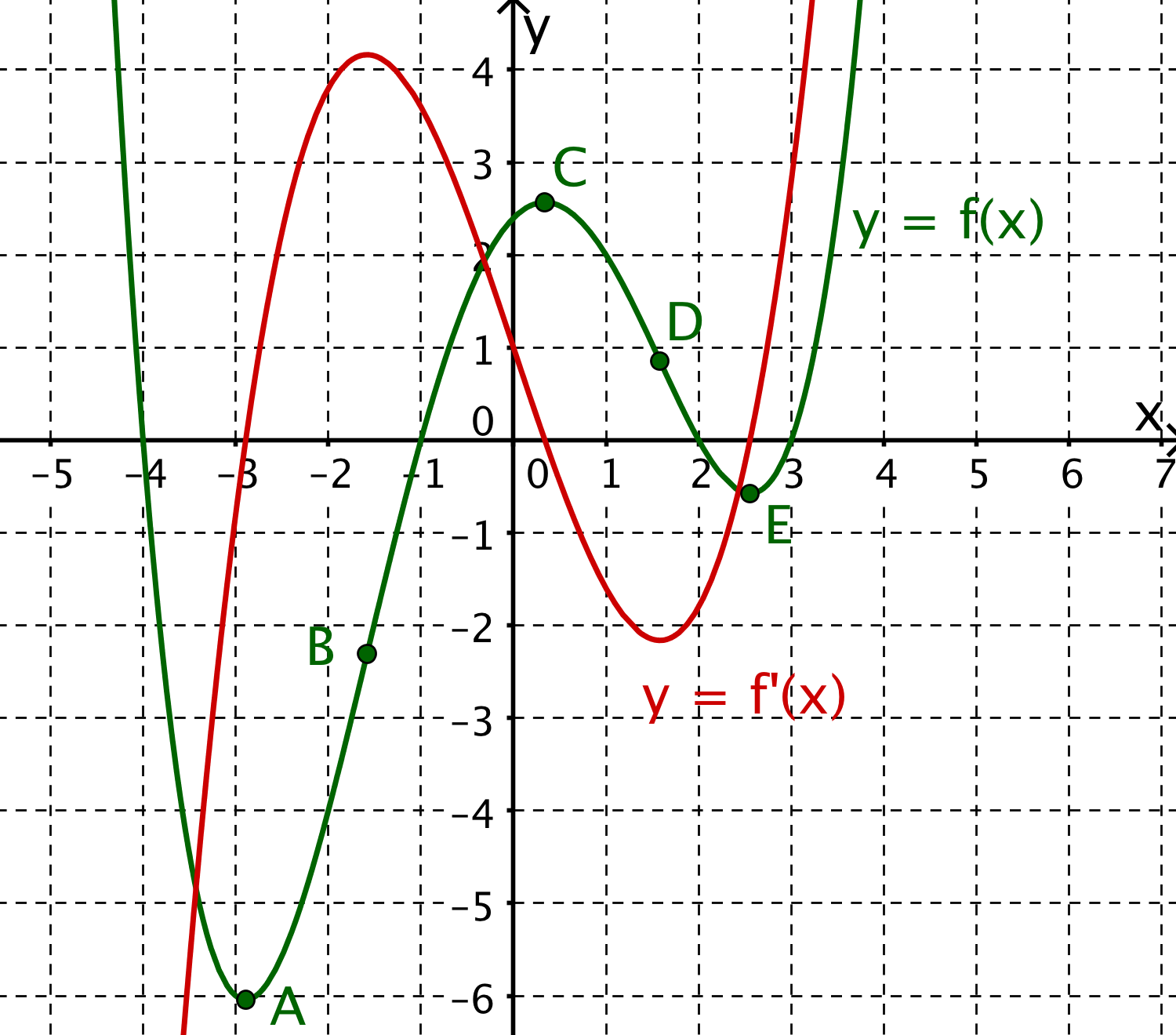
Graphisches Differenzieren einer ganzrationalen Funktion höheren Grades
Fertige durch graphisches Differenzieren eine Skizze der Ableitungsfunktion der nachfolgenden ganzrationalen Funktion 4. Grades.
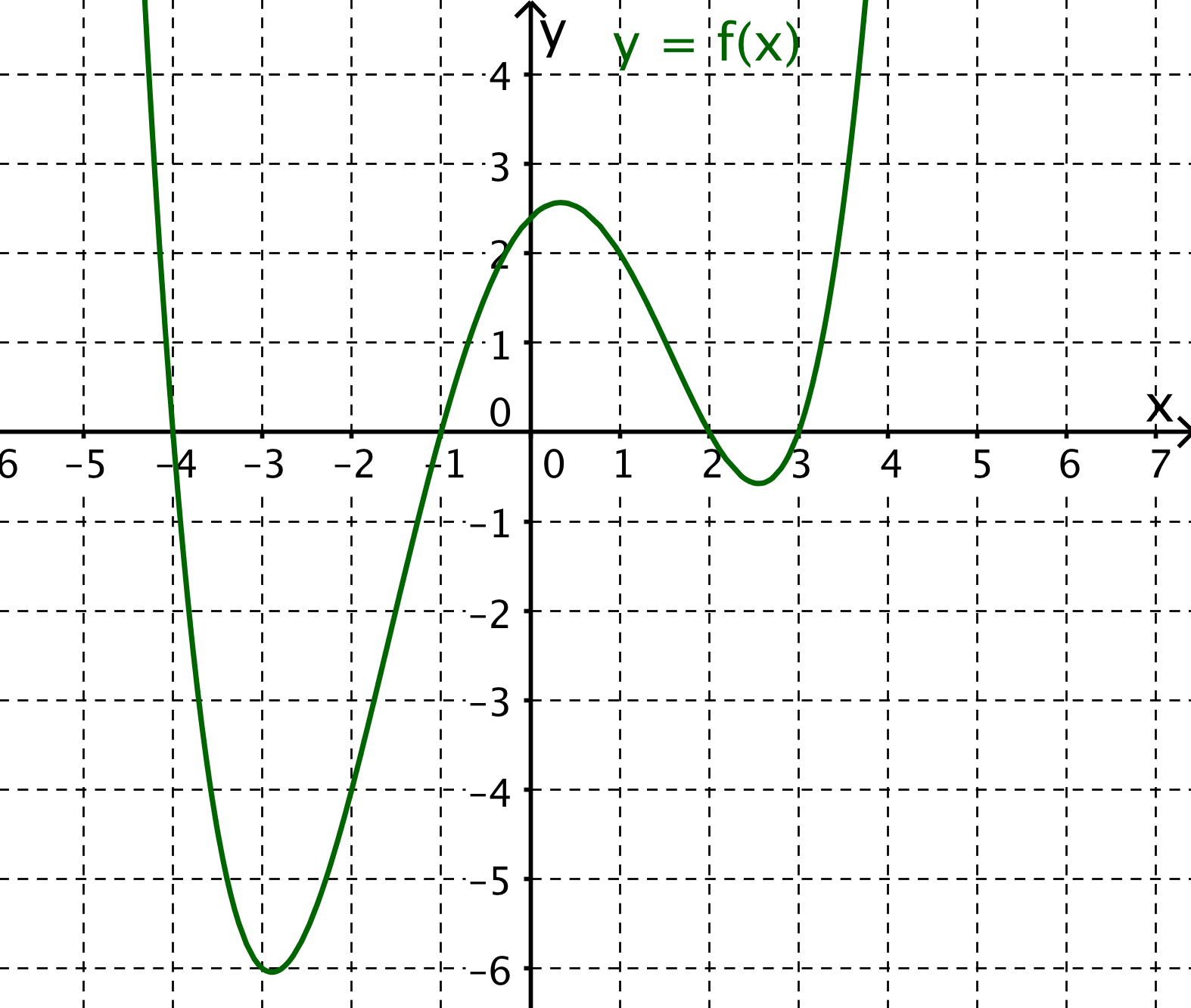
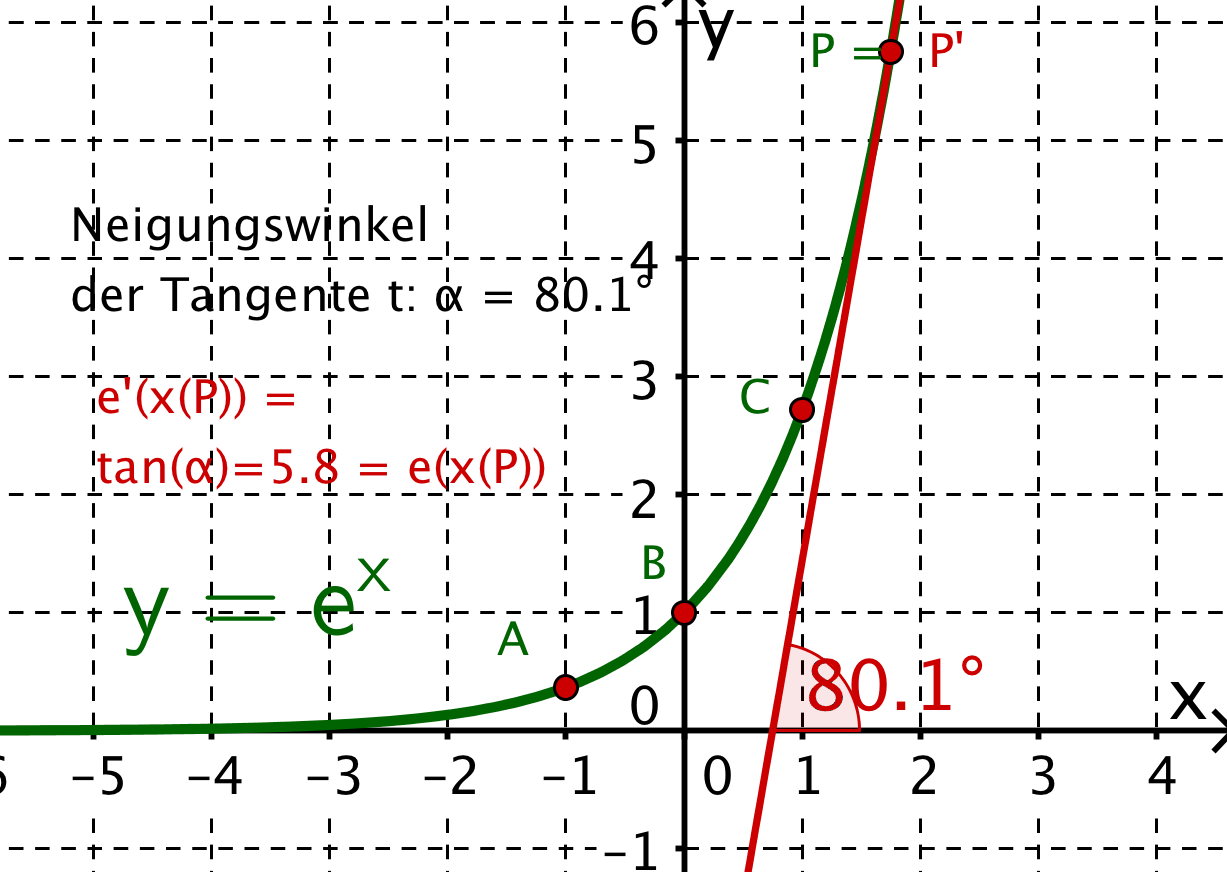
Graphisches Differenzieren der e-Funktion
Die e-Funktion ist für viele Anwendungsgebiete der Mathematik eine der wichtigsten Funktionen.
Graphisch gesehen ist sie aber eher eine besonders "langweilige" Funktion: ohne Nullstellen, ohne lokale Extrema und ohne Wendepunkte - einfach nur steigend.
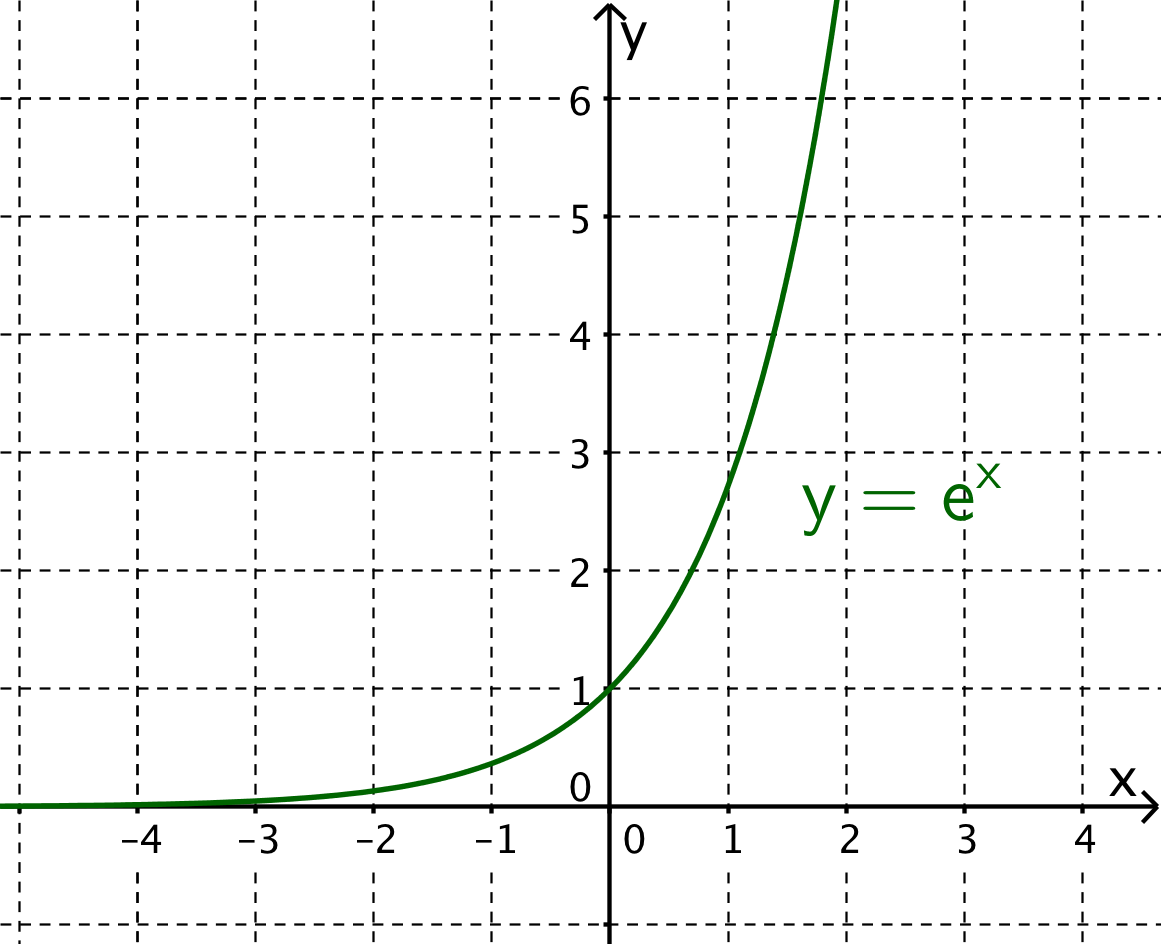
Welche überraschende Besonderheit der e-Funktion entdeckst du aber, wenn du dich um eine möglichst genaue Skizze beim graphischen Differenzieren der e-Funktion bemühst?
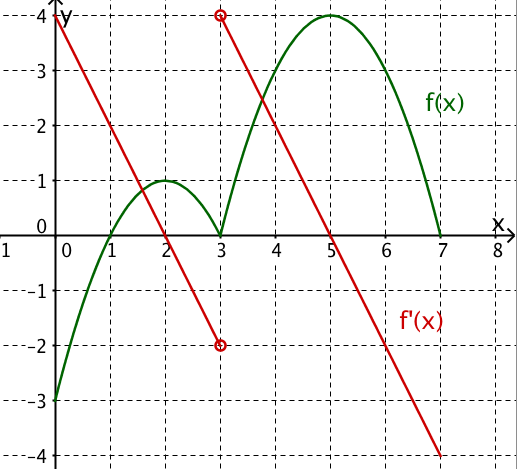
Graphisches Differenzieren einer abschnittsweise definierten Funktion
Die folgende Funktion ist graphisch zu differenzieren.
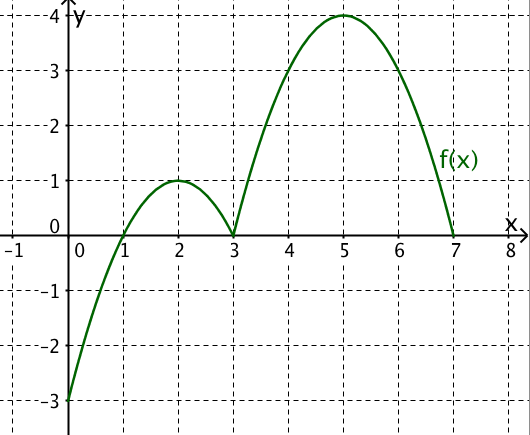
Klicke die richtige Lösung an!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?