1 Übersicht
Inhalt des Kurses
In diesem Kurs lernst du, wie man mit ganzen Zahlen rechnet. Behandelt werden zuerst Addition und Subtraktion mit dem Guthaben-Schulden-Modell und danach Multiplikation und Division.
Vorkenntnisse
Du solltest alle Grundrechenarten beherrschen und dich mit den ganzen Zahlen auskennen.
Kursdauer
Der Kurs dauert ungefähr 1,5 Stunden.
2 Das Minus
Du hast bereits einige Erfahrungen mit dem ""-Zeichen gemacht. Doch dieses Symbol kann je nach Situation sehr unterschiedlich sein. Betrachte beispielsweise folgende Ausdrücke:

Welche Unterschiede erkennst du zwischen den beiden Verwendungen von "" ?
Beschreibe in Worten, was folgender Ausdruck bedeuten könnte:
3 Vorzeichen und Rechenzeichen
Achtung:
Wenn zwei Zeichen in einer Rechnung unmittelbar hintereinander stehen, handelt es sich beim ersten immer um ein Rechenzeichen und beim zweiten um ein Vorzeichen.
Rechenzeichen
Beispiele: oder
Vor und hinter dem Rechenzeichen steht eine Zahl.
Es findet eine Rechnung statt: Minusrechnen (Subtraktion) oder Plusrechnen (Addition).
Es gibt ein Ergebnis (Differenz bzw. Summe).
Vorzeichen
Beispiele: oder
Wenn nur hinter dem Zeichen eine Zahl steht, handelt es sich um ein Vorzeichen.
Auch das "" kann als Vorzeichen auftreten.
Mit dem Vorzeichen wird gekennzeichnet, ob es sich um eine positive oder negative Zahl handelt
Bei positiven Zahlen wird das Vorzeichen "" meist weggelassen.
Merke: Zur besseren Lesbarkeit dürfen in Rechenausdrücken keine zwei Plus- oder Minuszeichen hintereinander kommen. Es werden entsprechend Klammern gesetzt.
Beispiel zur Klammersetzung:
4 Einführung ins Kontospiel
Das Kontospiel läuft wie das Bezahlen mit einem Bankkonto ab: Du kannst Geld bzw. Schulden aufnehmen oder abgeben.
Im Spiel wird das Geld, das du besitzt, durch Guthabenscheine ausgedrückt.
Hast du Schulden, wird das durch Schuldscheine ausgedrückt.

Ein Schuldschein und ein Guthabenschein heben sich gegenseitig auf.
Du kannst es dir z.B. so vorstellen: Du schuldest einem Freund einen Euro (einen Schuldschein). Du hast einen Euro in deinem Geldbeutel (also einen Guthabenschein). Wenn du dem Freund den Euro gibst, seid ihr quitt und du hast weder Schulden noch Guthaben.

Im Spiel kannst du Guthabenscheine bzw. Schuldscheine aufnehmen oder abgeben. Aufnehmen entspricht Plusrechnen und abgeben entspricht Minusrechnen.
Beispiel: Du hast drei Guthabenscheine.
Gibst du 2 davon ab, so hast du noch einen Guthabenschein. Du gibst ab, rechnest also Minus:
Nimmst du jetzt wieder vier Guthabenscheine auf, so hast du nun 5 Guthabenscheine. Du nimmst auf, rechnest also Plus:
5 Interaktives Kontospiel
Im Folgenden sollst du dich mit dem Spiel vertraut machen.Löse die Aufgaben.
6 Erkenntnisse des Kontospiels
Du hast gerade im Kontospiel folgende Aufgaben berechnet. Solltest du Probleme haben, kannst du gegebenenfalls auf der vorigen Seite das Spiel nochmal spielen.
Betrachten wir hier nun die neuen Fälle:
Wie du im Spiel gesehen hast, ist . Das ist also das gleiche wie bei . Deshalb kannst du folgern:
Du hast im Spiel gesehen: . Du siehst:
Du hast im Spiel gesehen: . Das ist offensichtlich das gleiche wie . Es gilt also auch:
7 Veränderung des Kontospiels
Auf der nächsten Seite steht dir das Kontospiel noch einmal als Rechenhilfe zur Verfügung. Jedoch sieht die Anwendung etwas anders aus, da es keine integrierten Aufgaben mehr gibt.
Vielleicht hast du auf den letzten Seiten schon bemerkt, dass sich die Bilanz nicht verändert, wenn du jeweils einen Guthaben- und einen Schuldschein aufnimmst.
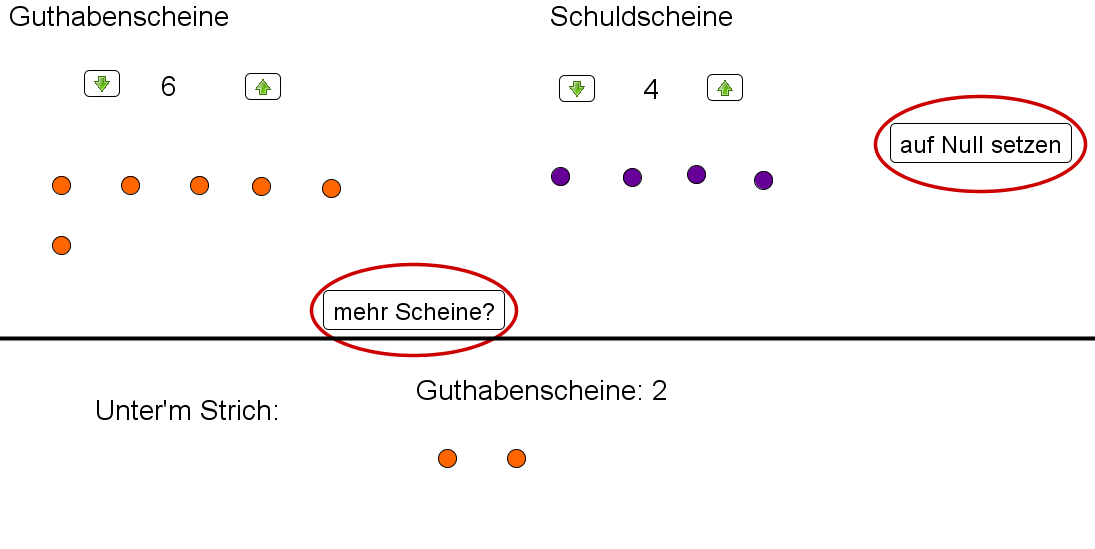
Neue Buttons:
mehr Scheine?:
Fügt eine Guthaben- und einen Schuldschein hinzu. "Unterm Strich" ändert sich nicht (wie oben bereits gesagt).
auf null setzen:
Alle Guthaben- und Schuldscheine werden gelöscht.
8 Aufgaben zum Addieren und Subtrahieren
Berechne folgende Aufgaben zu ganzen Zahlen.
Am Ende der Kursseite hast du die Möglichkeit, das Kontospiel als Hilfestellung zu nutzen.
Laden
Laden
Laden
9 Multiplikation mit ganzen Zahlen
Du erinnerst dich vielleicht an den Zusammenhang zwischen der Multiplikation und der Addition?
Man kann eine Multiplikation auch durch mehrere Additionen durchführen. Schau dir dieses Beispiel an:
"Plus mal Minus"
Auf dieselbe Art kannst du dir überlegen, wie man mit einer negativen Zahl multipliziert:
Wenn du auf die gleiche Art wie oben vorgehst, kannst du dir die Rechenregel selbst herleiten:
Du siehst: Am Betrag des Ergebnisses hat sich durch das Minus nichts geändert (auch ), aber am Vorzeichen: Das Ergebnis ist jetzt negativ.
"Minus mal Plus"
Wie immer soll beim Multiplizieren gelten:
Wenn beide Faktoren vertauscht werden, ändert sich das Ergebnis nicht. (Kommutativgesetz)
Deshalb kannst du auch für negative Zahlen folgern:
Rechenregel
10 Negative Zahl mal negative Zahl (1/2)
Inzwischen kannst du negative mit natürlichen Zahlen multiplizieren. Doch wie funktioniert das mit der Multiplikation von zwei negativen Zahlen?
Betrachte hierfür folgende Rechnungen.
Diese Rechnungen solltest du mit dem bisherigen Wissen aus dem Kurs nachvollziehen können.
Versuche dir nun zu überlegen, wie diese Reihe fortgesetzt werden könnte und was du für die beiden Fragezeichen einsetzen würdest, bevor du auf die nächste Kursseite klickst.
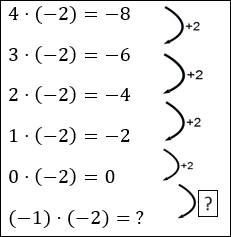
11 Negative Zahl mal negative Zahl (2/2)
Vielleicht bist du auf die korrekte Lösung (siehe rechts) gekommen.
Du kannst also daraus erkennen, dass und du könntest mit demselben Muster die Reihe fortsetzen:
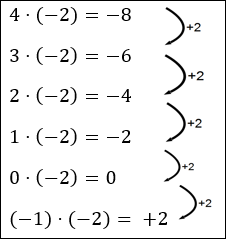
Daraus ergibt sich folgende Regel:
Also negative Zahl mal negative Zahl ergibt eine positive Zahl.
12 Beispielaufgaben zur Multiplikation
Beispielaufgabe 1:
Berechne
Berechne zuerst .
Da jedoch einer der beiden Faktoren negativ war, ist auch das Ergebnis negativ.
Erinnere dich: "Plus mal Minus ist Minus"
Beispielaufgabe 2:
Berechne
Wie immer gilt "Punkt vor Strich". Berechne zuerst die beiden Produkte.
Beachte hier:
"Minus mal Plus ist Minus" und
"Minus mal Minus ist Plus"
Addiere nun die beiden Produktwerte.
13 Aufgaben zur Multiplikation
Berechne folgende Ausdrücke:
Achte auf die Rechenregeln und die Vorzeichen!
Laden
Laden
Laden
Laden
14 Division ganzer Zahlen
Jetzt, wo du dich mit der Multiplikation beschäftigt hast, ist die Division nicht mehr schwer.
Aus den natürlichen Zahlen weißt du, dass . Eine solche Division macht die Multiplikation also rückgängig.
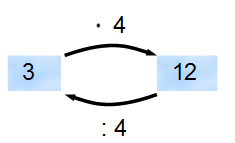
Du kennst bereits das Ergebnis einer Multiplikation von zwei ganzen Zahlen. So weißt du: .
Was könnte man bei für das Fragezeichen einsetzen?
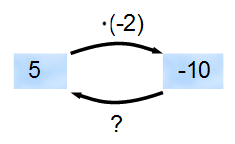
Auf gleiche Weise folgt mit

15 Division ganzer Zahlen
Wir haben auf der letzten Kursseite gesehen:
Aus diesen Ergebnissen folgt:
Wie bei der Multiplikation bedeutet das:
Veränderst du ein Vorzeichen bei einer Division, verändert sich das Vorzeichen des Ergebnisses.
Beispiel:
6 als Quotient der positiven Zahlen 12 und 2
Hier wurde ein Vorzeichen verändert (im Vergleich zur ersten Aufgabe). Wie du siehst, hat sich das Ergebnis um ein Minus verändert.
Hier wurde ein Vorzeichen (im Vergleich zur zweiten Aufgabe) verändert.
Das Ergebnis hat sich ..
..im Vergleich zu Aufgabe zwei um ein Vorzeichen verändert.
..im Vergleich zu Aufgabe eins nicht verändert.
16 Aufgaben zur Division ganzer Zahlen
Berechne die Quotienten mit den Rechenregeln
Laden
Laden
Laden
17 Zusammenfassung
Für alle Rechenarten gilt:
Es sind auch negative Ergebnisse möglich.
Addition/ Subtraktion
Stehen und vor der gleichen Zahl, so kannst du sie durch ein ersetzen:
Stehen und vor der gleichen Zahl, so kannst du sie durch ein ersetzen:
Multiplikation/ Division
"Plus mal Minus ist Minus" und "Minus mal Plus ist Minus".
"Minus mal Minus ergibt Plus."
Für Division gilt: "Plus durch Minus ist Minus" und "Minus durch Plus ist Minus",
sowie"Minus durch Minus ergibt Plus".
18 Zeig, was du kannst!
Berechne mit den neu gelernten Formeln:
Laden
Laden
Laden
Laden
Laden
