Aufgaben zu relativen Häufigkeit

Bei einer Schulaufgabe ergab sich für die Noten folgende Verteilung:

Note	1	2	3	4	5	6
Anzahl	3	2	9	6	7	2

Berechne die relative Häufigkeit der einzelnen Noten!

Für diese Aufgabe benötigst Du folgendes Grundwissen: relative Häufigkeit

Die Gesamtzahl der Schüler kann aus der Anzahl der einzelnen Noten ermittelt werden.

$3+2+9+6+7+2= 29$

Berechne für jede Note die relative Häufigkeit.

Note	relative Häufigkeit
$1$	$\frac3{29}=0{,}1034\approx10\,\%$
$2$	$\frac2{29}=0{,}06897\approx7\,\%$
$3$	$\frac9{29}=0{,}3103\approx31\,\%$
$4$	$\frac6{29}=0{,}2069\approx21\,\%$
$5$	$\frac7{29}=0{,}2414\approx24\,\%$
$6$	$\frac2{29}=0{,}06897\approx7\,\%$

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

2
In einem Hörsaal sitzen 150 Studenten. 110 von ihnen sprechen nur Englisch, 20 nur Spanisch und 15 sprechen beide Sprachen.
1. Wie groß ist die relative Häufigkeit der Studenten, die mindestens eine der beiden Sprachen sprechen?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
  Bilde die Summe der Studenten, die Englisch und/oder Spanisch sprechen, geteilt durch die Gesamtanzahl der Studenten.
  Relative Häufigkeit:
  $\frac{110+20+15}{150}=\frac{145}{150}\approx\mathbf{96}{\boldsymbol,}\mathbf7\,\boldsymbol\%$
  Also sprechen ungefähr 96,7 % der Studenten mindestens eine der beiden Sprachen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Wie groß ist die relative Häufigkeit der Studenten, die keine der beiden Sprachen sprechen?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Gegenereignis
  $1-\frac{110+20+15}{150}=1-\frac{145}{150}$
  Schreibe auf einen Bruch und wandle am Ende in Prozent um.
  $1-\frac{145}{150}=\frac{150-145}{150}=\frac{5}{150}=\frac{1}{30}\approx3{,}33\,\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bilde die Summe der Studenten, die Englisch und/oder Spanisch sprechen, teile sie durch die Gesamtanzahl der Studenten und ziehe das Ergebnis von 1 ab.
3
Ein Viertel aller Schüler einer Klasse hat einen Hund, die Hälfte der Schüler hat eine Katze. Kein Schüler hat beide Haustiere. Ermittle den Anteil der Schüler, die keines dieser Haustiere haben.
$0$ Schüler hat keine Haustiere.
Die Hälfte $\left(\dfrac12\right)$ der Schüler hat keine Haustiere.
Ein Viertel $\left(\dfrac14\right)$ der Schüler hat keine Haustiere.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
Lösung durch eine Gleichung
Niemand in der Klasse hat beide Haustiere. Deshalb gibt es nur drei Situationen: Hund, Katze oder kein Haustier.
Die Summe der Anteile muss $100 ~\%$ , also $1$ ergeben.
$x$ bezeichnet den Anteil der Kinder, die keines dieser Haustiere haben.
$x+\underbrace{\dfrac{1}{4}}_{\text{Anteil mit Hund}}+\underbrace{\dfrac{1}{2}}_{\text{Anteil mit Katze}}=1$
$\displaystyle x$ $=$ $\displaystyle 1-\dfrac{3}{4}$
↓
nach x auflösen
$\displaystyle x$ $=$ $\displaystyle \dfrac14=0{,}25=25\,\%$
Darstellung in der Vierfeldertafel
Wenn du die Vierfeldertafel schon kennst, kannst du die Situation auch damit darstellen.
$H$
$\overline{H}$
$K$
0
$\frac{1}{2}$
$\frac{1}{2}$
$\overline K$
$\frac{1}{4}$
$\color{red}\frac{1}{4}$
$\frac{1}{2}$
$\frac{1}{4}$
$\frac{3}{4}$
1
(H: hat Hund, K: hat Katze)
Beim Ausfüllen der Vierfeldertafel ergibt sich der Wert $\frac{1}{4}$ für den Anteil "Kein Hund und keine Katze", bzw. $\bar{K}\wedge\bar{H}$ .
Beachte, dass kein Schüler beide Haustiere hat.
Du kannst die Aufgabe deshalb auch ohne eine Vierfeldertafel lösen.
4
In einer Schulklasse sind 28 Schüler, darunter 12 Mädchen. Bei einer Umfrage gaben 7 Mädchen und 8 Buben an, Sport sei ihr Lieblingsfach.
Ist das Fach Sport laut der Umfrage bei den Mädchen oder bei den Jungen in der Klasse beliebter?
Sport ist bei den Jungs beliebter.
Sport ist bei den Mädchen beliebter.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
Berechne Relative Häufigkeit
Anzahl Mädchen in der Klasse $=12$
Anzahl Jungen in der Klasse $=28-12=16$
Relative Häufigkeit der Mädchen, die am liebsten Sport mögen $=\frac7{12}\approx58\,\%$
Relative Häufigkeit der Jungen, die am liebsten Sport mögen $=\frac8{16}=\frac12=50\,\%$
$\Rightarrow$ Sport ist bei den Mädchen insgesamt beliebter.

	$H$	$\overline{H}$
$K$	0	$\frac{1}{2}$	$\frac{1}{2}$
$\overline K$	$\frac{1}{4}$	$\color{red}\frac{1}{4}$	$\frac{1}{2}$
	$\frac{1}{4}$	$\frac{3}{4}$	1

Würfle 100-mal und bestimme die relative Häufigkeit der Augenzahl 6 für

die ersten 20,
die zweiten 20,
die dritten 20,
die vierten 20 und
die fünften 20 Würfe.

Für diese Aufgabe benötigst Du folgendes Grundwissen: relative Häufigkeit

Um die relative Häufigkeit deines Ergebnisses zu bestimmen, rechnest du allgemein:

\displaystyle \mathrm{\frac{Anzahl\ der\ Zahl\ 6}{Wurfanzahl}}

Beispielsweise könnte dein Ergebnis so aussehen:

Würfe	Anzahl der 6er	relative Häufigkeit
1 - 20	2	$\frac2{20}=0{,}1=10\,\%$
21 - 40	6	$\frac6{20}=0{,}3=30\,\%$
41 - 60	4	$\frac4{20}=0{,}2=20\,\%$
61 - 80	0	$\frac0{20}=0\,\%$
81 - 100	10	$\frac{10}{20}=0{,}5=50\,\%$

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

6
Als Hausaufgabe sollten die Schüler der Klasse 6 b mindestens 100-mal würfeln und die relativen Häufigkeiten, mit denen die einzelnen Augenzahlen aufgetreten sind, mithilfe einer Tabelle oder eines Diagramms darstellen.
Am nächsten Tag vergleichen Manfred, Peter, Klaus und Christian ihre Ergebnisse:
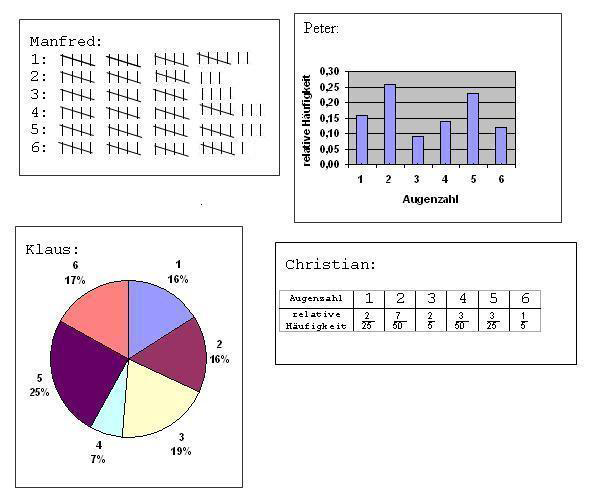
1. Nach einem kurzen Blick in Manfreds Heft sagt Christian: „Du hast wohl in der letzten Mathestunde nicht richtig aufgepasst!“ Wie kommt er dazu?
  Manfred hat in der letzten Mathestunde Quatsch gemacht.
  Manfred hat die relativen Häufigkeiten dargestellt.
  Manfred hat die absoluten Häufigkeiten dargestellt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
  Manfred hat nicht die relativen Häufigkeiten, sondern die absoluten Häufigkeiten angegeben.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Klaus hat genau 200-mal gewürfelt. Wie oft hat er eine „6“ geworfen?
  Mal
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
  Klaus hat in $17 \%$ der Fälle eine $6$ gewürfelt. Du hast also die relative Häufigkeit gegeben, diese musst du jetzt mit der Gesamtanzahl an Würfen multiplizieren, um die absolute Häufigkeit zu erhalten:
  Klaus hat also insgesamt $34$ Mal eine $6$ gewürfelt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Peter betrachtet kurz die Diagramme und verkündet dann laut: „Christian hat von uns vier den besten Würfel. Bei ihm fällt am häufigsten die Sechs.“ Wie kommt Peter zu dieser Aussage? Glaubst auch du, dass Christian den besten Würfel hat?
  Christian hat wirklich den besten Würfel.
  Peter behauptet das, weil bei Christian die relative Häufigkeit mit $\frac15$ am größten ist.
  Christian hat nicht unbedingt einen besseren Würfel.
  Christian hat am meisten die 6 geworfen, weil er sich am meisten angestrengt hat.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
  Christian hat mit $\dfrac{1}{5}=0{,}2=20\,\%$ den höchsten Anteil von Würfen mit 6 Augen. Bei vielen Würfelspielen wäre er also im Vorteil.
  Ob Christian den besten Würfel hat, kann man aber so nicht sagen:
  Würfeln ist ein Zufallsexperiment, d.h. es ist "normal", dass nicht jeder gleich oft die 6 würfelt
  Die Jungen haben nicht gleich oft gewürfelt, das macht das Vergleichen noch schwieriger
  Es ist nicht in jedem Spiel besser viele 6er zu würfeln.
  Du hast noch weitere Ideen, warum Christian im Vorteil ist oder vielleicht auch nicht? Schreib sie in die Kommentare! :-)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7
30 Würfe mit einem Würfel ergaben folgendes Ergebnis:
Augen
1
2
3
4
5
6
Anzahl
4
6
2
6
5
7
Überprüfe mit diesen Zahlen die 3. Eigenschaft von relativer Häufigkeit
$h_n(A \cup B) = h_n(A) + h_n(B) - h_n(A \cap B)$
durch Rechnen.
Benutze dazu diese Ereignisse:
$A$ : Die Menge der Würfe mit maximal 3 Augen.
$B$ : Die Menge der Würfe mit gerader Augenzahl.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
$A=\{1{,}2,3\}, B=\{2{,}4,6\}$
Bestimme die Mengen A und B aus dem Text.
$h_n(A\cup B)=\frac{H(A\cup B)} {30}=\frac{H(\{1{,}2,3{,}4,6\})} {30}=\frac{4+6+2+6+7} {30}=\frac{25} {30}$
Berechen die relative Häufigkeit von $A \cup B$ .
$h_n(A)=\frac{H(A)} {30}=\frac{H(\{1{,}2,3\})} {30}=\frac{4+6+2} {30}=\frac{12} {30}$
Berechen die relative Häufigkeit von A.
$h_n(B)=\frac{H(B)} {30}=\frac{H(\{2{,}4,6\})} {30}=\frac{6+6+7} {30}=\frac{19} {30}$
Berechen die relative Häufigkeit von B.
$h_n(A\cap B)=\frac{H(A\cap B)} {30}=\frac{H(\{2\})} {30}=\frac{6} {30}$
Berechen die relative Häufigkeit von $A \cap B$ .
$h_n(A \cup B) = h_n(A) + h_n(B) - h_n(A \cap B)$ $\Leftrightarrow\frac{25} {30}=\frac{12} {30}+\frac{19} {30}-\frac{6} {30}$ $\Leftrightarrow\frac{25} {30}=\frac{25} {30}$
Setze in die Formel ein.
Gleichheit bestätigt die Formel.
Überprüfen der 3ten Rechenregel vom Artikel "Relative Häufigkeit" anhand eines Beispiels

Augen	1	2	3	4	5	6
Anzahl	4	6	2	6	5	7

In einer Schulklasse ergaben sich bei einer Mathematikschulaufgabe folgende Noten:

Note	1	2	3	4	5	6
Anzahl der Schüler	1	4	11	8	5	1

Als Notendurchschnitt gibt der Lehrer $3{,}5$ an.

Prüfe, ob der Notendurchschnitt exakt angegeben oder gerundet wurde.

Der Notendurchschnitt wurde gerundet.
Der Notendurchschnitt wurde exakt angegeben.

Ermittle die relativen Häufigkeiten der einzelnen Noten und erstelle ein geeignetes Diagramm zur Darstellung der Notenverteilung.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
Ermittle die relative Häufigkeit der jeweiligen Note, indem du die Häufigkeit der Note durch die Gesamtanzahl der Schüler dividierst.
Note 1: $\frac1{30}=0{,}0\overline3=3{,}\overline3\,\%$
Note 2: $\frac4{30}=0{,}1\overline3=13{,}\overline3\,\%$
Note 3: $\frac{11}{30}=0{,}3\overline6=36{,}\overline6\,\%$
Note 4: $\frac8{30}=0{,}2\overline6=26{,}\overline6\,\%$
Note 5: $\frac5{30}=0{,}1\overline6=16{,}\overline6\,\%$
Note 6: $\frac1{30}=0{,}0\overline3=3{,}\overline3\,\%$
Diagramm:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \frac{1\cdot1+2\cdot4+3\cdot11+4\cdot8+5\cdot5+6\cdot1}{1+4+11+8+5+1}$	$=$	$\displaystyle \frac{105}{30}$
	↓	Rechne aus und vereinfache.
	$=$	$\displaystyle 3{,}5$

$\displaystyle x$	$=$	$\displaystyle 1-\dfrac{3}{4}$
	↓	nach x auflösen
$\displaystyle x$	$=$	$\displaystyle \dfrac14=0{,}25=25\,\%$

Aufgaben zu relativen Häufigkeit

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösung durch eine Gleichung

Darstellung in der Vierfeldertafel

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Diagramm:

Hast du eine Frage oder Feedback?