Rechnen mit Einheiten

Bei Anwendungsaufgaben in der Mathematik rechnet man oft nicht nur mit Zahlen, sondern auch mit Einheiten, wie beispielsweise Kilogramm, Liter, Meter… Davon sollte man sich aber nicht abschrecken lassen, da sich Einheiten bei den Rechnungen wie Zahlen behandeln lassen. Entscheidend ist, dass man darüber nachdenkt, welche Einheit rauskommen muss und ob diese dann auch Sinn ergibt. Dabei ist z. B. bei der Berechnung von Flächen eine Größe wie $m^{2}$ sinnvoll, wohingegen $\min^{2}$ keinen Sinn ergibt.

Hier wird deutlich, dass man Einheiten mathematisch nicht wie Zahlen behandeln kann.

VorsichtGleiche Einheiten

Bevor man anfängt loszurechnen, muss man unbedingt darauf achten, dass die Größen einheitlich sind. Größen mit unterschiedlichen Einheiten können nicht bei jeder Rechenart sinnvoll verarbeitet werden.

Einheiten addieren/ subtrahieren

Wenn man Einheiten addiert/ subtrahiert, verändern sich zwar die Ziffern, jedoch nicht die Einheiten. Diese bleiben gleich. Damit man beim Rechnen nicht verwirrt ist, kann man sich dazu die Einheit erst gedanklich wegdenken, die Ziffern addieren/ subtrahieren und dann zum Endergebnis wieder die Einheit hinzufügen.

Man kann diese Schritte mit allen Einheiten durchführen. Also mit Gewichten $t, kg, g, \dots$ , Größen $km, m, cm, \dots$ , Mengen $l, ml, \dots$ und Zeitangaben $h, \min, s, \dots$ . Hier ergibt das alles Sinn, d.h. dass die Rechnung logisch ist und man etwas mit dem Ergebnis anfangen kann.

Beispiel

$3 m + 4 m = 7 m$
$15 ml - 10 ml = 5 ml$
$7 \min + 4 \min - 10 \min = 1 \min$

Einheiten multiplizieren

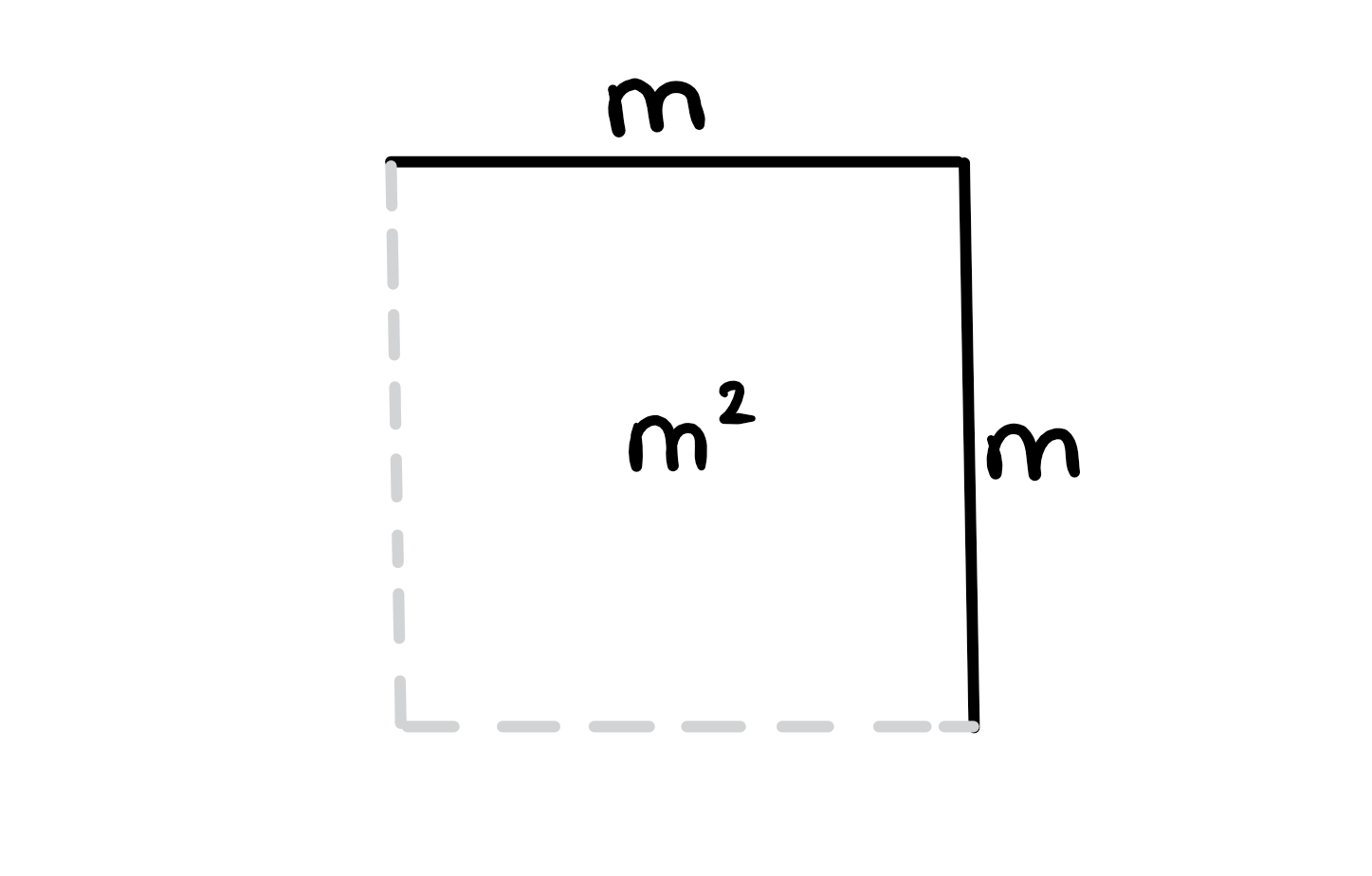
Beim Multiplizieren von Einheiten kann man sich das Konzept am besten anhand von der Flächenberechnung vorstellen. Wenn man z. B. eine Bodenfliese mit $1 m$ Kantenlänge hat, rechnet man:

1 m \cdot 1 m = 1 m^{2}

und erhält so die Fläche der Fliese, nämlich $1 m^{2}$ . Oder anders betrachtet:

1 m \cdot 1 m = 1 \cdot 1 \cdot m \cdot m = 1 m^{2}

Diese Überlegung kann man fortführen und die entstandene neue Einheit $m^{2}$ bspw. mit $m$ oder auch $m^{2}$ multiplizieren, um so neue Größen zu erzeugen. Das sieht dann folgendermaßen aus:

1 m^{2} \cdot 1 m = 1 m^{3}

1 m^{2} \cdot 1 m^{2} = 1 m^{4}

Danach kann man diese Rechnung erneut wie oben ausführen und gelangt dann so zu allen denkbaren Möglichkeiten. Es ist sogar $m^{1000}$ möglich. Zum Glück braucht man so etwas erst im Mathestudium ;-)

Dass, wie gesagt, Einheiten mathematisch nicht wie Zahlen behandelt werden dürfen, zeigt sich auch hier. Ein Quadratmeter mit einem Quadratmeter zu multiplizieren, ist nicht anschaulich. Unter dem Ergebnis " $m^{4}$ " kann man sich nichts vorstellen.

Das geht prinzipiell mit allen Einheiten, die man bereits bei Einheiten addieren/ subtrahieren schon angesprochen hat. Also mit $kg, m$ , aber auch mit Zeitangaben wie $\min$ und $s$ . Hier ergibt das allerdings nicht immer alles Sinn. Das bedeutet, dass man, jedenfalls in der Mathematik, nicht mit $k g^{2}$ rechnet. Hieran kann man dann auch ziemlich schnell erkennen, ob man richtig gerechnet bzw. umgeformt hat oder ob sich ein Fehler eingeschlichen hat.

Beispiel

Überlege, welchen Wert und welche Einheit das Ergebnis besitzt. Ergibt die Einheit anschaulich einen Sinn?

Entscheide dich zuerst für eine Einheit. Wir nehmen hier Meter.
	↓
$200 dm \cdot 10 m^{2} \cdot 0,1 km$	$=$	$20 m \cdot 10 m^{2} \cdot 100 m$
	↓	Überlege nun, wie du vielleicht zuerst $20 m$ und $100 m$ multiplizierst. Lasse die $10 m^{2}$ dabei zunächst stehen.
	$=$	$2000 m^{2} \cdot 10 m^{2}$
	↓	Wenn $m \cdot m = m^{2}$ , was ergibt dann $m^{2} \cdot m^{2}$ ?
	$=$	$20000 m^{4}$

Einheiten dividieren

Beim Dividieren von Einheiten kommt es darauf an, so viel zu kürzen wie möglich. Man schreibt dabei am besten die Rechnung als Bruch. So kann man am leichtesten erkennen, was sich wegkürzen lässt und was nicht. Auch hier ist es wichtig, dass man alles zuerst auf eine einheitliche Größe umrechnet.

Beispiel

Wie breit ist ein Rechteck mit der Fläche $A = 10 m^{2}$ und der Länge $l = 5 m$ ?

A = l \cdot b

Stelle nach der Breite $b$ um.

$\Rightarrow b = \frac{A}{l}$

Setze nun die Werte ein.

b = \frac{10 m^{2}}{5 m}

Überlege nun, welche Einheit herauskommen soll. Richtig, die Breite misst man in Metern. Ist doch auch logisch, dass dann $\frac{m^{2}}{m} = \frac{m \cdot m}{m} = m$ ergibt, findest du nicht? Bei Produkten dürfen wir ja kürzen.

b = 2 m

Checkliste

Achte auf einheitliche Größen.
Schaue nach deiner Rechenoperation.
Rechne geschickt aus. Achte auf das Wegkürzen/ Multiplizieren von deinen Größen.

Sonderfall: Nachkommastellen

Es kann sein, dass eine Aufgabe nicht nur mit ganzen Zahlen gestellt ist. Dabei können auch Nachkommastellen vorkommen. Wenn man vor einer solchen Aufgabe steht, sollte man auf jeden Fall nicht schnell das Heft zu machen. Es geht ganz einfach: Man rechnet alle Größen auf die kleinste Einheit um, um unnötig viele Kommas zu vermeiden. Dann rechnet man wie oben gelernt weiter. Am Ende vereinfacht man das Endergebnis, indem man auf eine größere Einheit erneut umrechnet.

Beispiel

Vereinheitliche deine Größen, indem du in die kleinste Einheit umrechnest.
	↓
$13,5 dm + 12 cm$	$=$	$135 cm + 12 cm$
	↓	Da die Einheiten gleich sind und es sich um eine Addition handelt, kannst du ganz einfach das Ergebnis ausrechnen.
	$=$	$147 cm$
	↓	Rechne das Ergebnis auf eine größere Einheit um. Am besten so lange, bis nur eine Stelle vor dem Komma steht.
	$=$	$14,7 dm$
	$=$	$1,47 m$

= 14,7 dm = 1,47 m

Hier kann man auch viele Aufgaben unterschiedlichen Schwierigkeitsgrades zur Umrechnung von Volumeneinheiten finden.

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Kurse

Einheiten

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?