Teil B - lernen mit Serlo!

Dieser Inhalt wurde gelöscht.

Lösung zu Teilaufgabe B 2.1

Lösung zu Teilaufgabe B 2.2

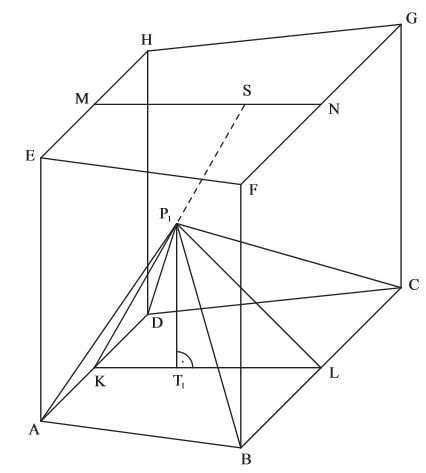
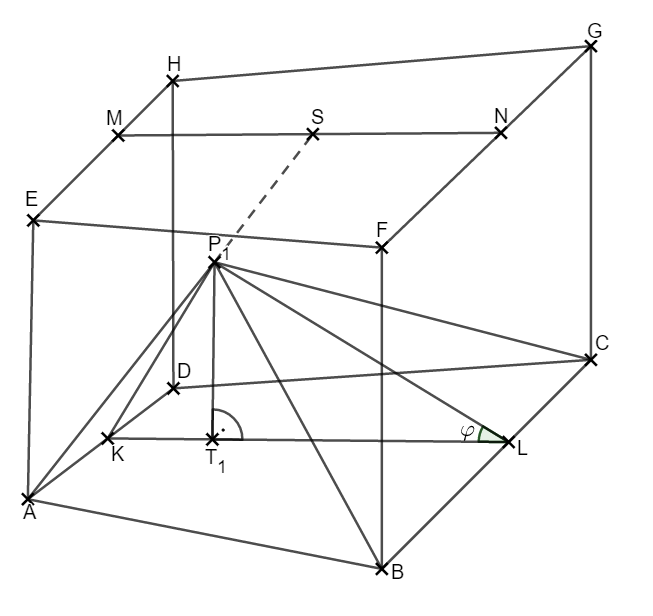
Aus der Aufgabenstellung weißt du, dass der Punkt $M$ der Mittelpunkt der Strecke $[E H]$ und $N$ der Mittelpunkt der Strecke $[F G]$ ist.

Außerdem soll $S$ auf der Strecke $[M N]$ liegen, wobei $S N = 2 cm$ gilt.

Als Erstes kannst du also die Punkte $M$ und $N$ sowie die Strecke $[M N]$ einzeichnen.

Danach zeichnest du den Punkt $S$ genau $2 cm$ links vom Punkt $N$ auf der Strecke $[M N]$ ein.

Jetzt kannst du den Winkel $∢ K L P_{1} = φ = 45 °$ in dein Schrägbild einzeichnen.

Skizze des Schiefbilds mit der Geraden MN

Nun musst du noch den Winkel $∢ L K S$ berechnen.

Dafür nutzt du die Tangensbeziehung

\tan (α) = \frac{Gegenkathete}{Ankathete} .

Um die Tangensbeziehung verwenden zu können, benötigst du einen rechten Winkel. Um diesen zu erhalten, zeichnest du zunächst den Lotfußpunkt $S^{'}$ von $S$ auf der Strecke $[K L]$ ein.

Der Punkt $S^{'}$ liegt nun $2 (cm)$ von $L$ entfernt.

Es gilt also $S^{'} L = 2 cm$ .

Mit $K L = 6 cm$ folgt dann:

$K S^{'} = 6 cm - 2 cm = 4 cm$

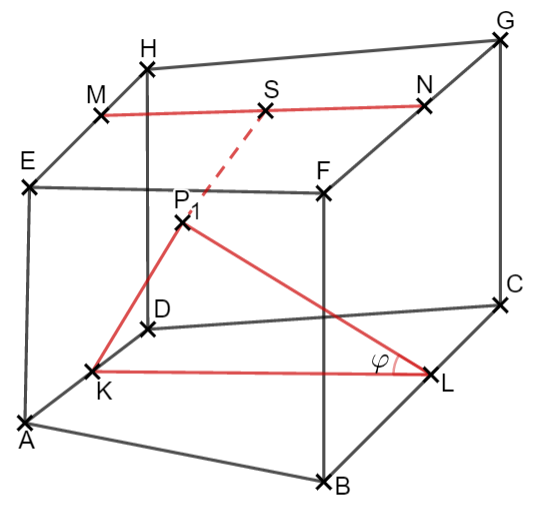
Vielleicht hast du bereits bemerkt, dass der Winkel $∢ L K S$ dem Winkel $∢ S^{'} K S$ entspricht und dass die Strecke $[S S^{'}]$ genauso lang ist wie die Strecke $[A E]$ .

Es gilt also $S S^{'} = 7 cm$ .

Anwenden der Tangensbeziehung liefert nun:

$\tan (∢ L K S) = \tan (∢ S^{'} K S) = \frac{S S^{'}}{K S^{'}} = \frac{7}{4} = 1,75$ .

Nun löst du die Gleichung nach dem Winkel $∢ L K S$ auf. Dafür benötigst du die Umkehrfunktion des Tangens, nämlich den Arcustangens.

Auflösen liefert ungefähr:

$\tan (∢ L K S)$	$=$	$1,75$	$\arctan (\cdot)$
$∢ L K S$	$=$	$\arctan (1,75)$
	↓	Berechne.
	$=$	${60,26}^{\circ}$

Lösung zu Teilaufgabe B 2.3

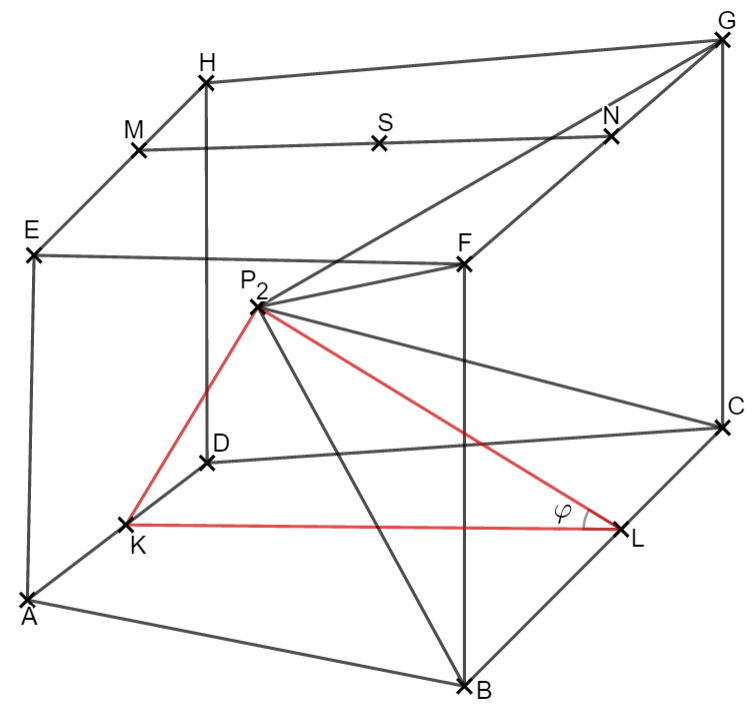
In dieser Teilaufgabe arbeitest du mit dem Sinussatz.

Zuerst betrachtest du das Dreieck $K L P_{n}$ und siehst, dass es nicht rechtwinklig ist. Daher kannst du in diesem Fall die Sinus-, Kosinus- und Tangensverhältnisse nicht verwenden.

Dafür ist der Sinussatz anwendbar. Dieser besagt, dass in einem Dreieck alle drei Verhältnisse "Seitenlänge dividiert durch Sinus des gegenüberliegenden Winkels" gleich sind:

$\frac{a}{\sin (α)} = \frac{b}{\sin (β)} = \frac{c}{\sin (γ)}$

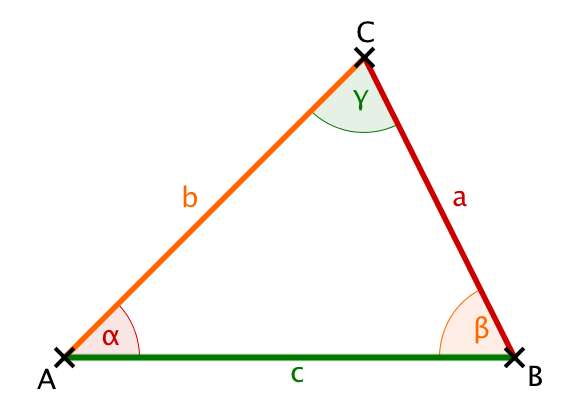
Geogebra File: https://assets.serlo.org/legacy/6492_iZV9VMFFJJ.xml

In dieser Teilaufgabe gilt also mit dem Sinussatz:

\frac{K L}{\sin (∢ K P_{n} L)} = \frac{L P_{n}}{\sin (∢ L K S)} .

Die Innenwinkelsumme des Dreiecks $K L P_{n}$ beträgt immer $180^{\circ}$ .

Damit kannst du den Winkel $∢ K P_{n} L$ bestimmen.

Mit $∢ L K S = ∢ L K P_{n}$ und $φ_{1} = ∢ L K P_{n}$ gilt:

$∢ K P_{n} L$	$=$	$180^{\circ} - ∢ L K S - ∢ P_{n} L K$
	$=$	$180^{\circ} - ∢ L K P_{n} - ∢ P_{n} L K$
	$=$	$180^{\circ} - φ_{1} - ∢ P_{n} L K$

Nun löst du die obige Verhältnisgleichung nach $L P_{n}$ auf:

$\frac{K L}{\sin (∢ K P_{n} L)}$	$=$	$\frac{L P_{n}}{\sin (∢ L K S)}$	$\cdot \sin (∢ L K S)$
$L P_{n}$	$=$	$\sin (∢ L K S) \cdot \frac{K L}{\sin (∢ K P_{n} L)}$
	↓	$∢ L K S = ∢ L K P_{n}$
	$=$	$\sin (∢ L K P_{n}) \cdot \frac{K L}{\sin (∢ K P_{n} L)}$

Jetzt kannst du dein Ergebnis aus Teilaufgabe B 2.2 $φ_{1} = ∢ L K P_{n} = {60,26}^{\circ}$ einsetzen.

Mit $K L = 6 (cm)$ und obigem Ergebnis erhältst du für $φ = ∢ P_{n} L K$ :

$L P_{n} (φ)$	$=$	$\sin ({60,26}^{\circ}) \cdot \frac{K L}{\sin (180^{\circ} - {60,26}^{\circ} - φ)}$
	↓	Wende die Supplementbeziehung an.
	$=$	$\sin ({60,26}^{\circ}) \cdot \frac{6}{\sin ({60,26}^{\circ} + φ)}$
	↓	Berechne
	$=$	$\frac{5,21}{\sin ({60,26}^{\circ} + φ)} cm$

Hier hast du die allgemeingültige Supplementbeziehung $\sin (180^{\circ} - α) = \sin (α)$ verwendet.

Die Länge $L P_{n} (φ)$ nimmt ihren kleinsten Wert an, wenn der Nenner möglichst groß ist.

Gesucht ist also das $φ$ , für das $\sin ({60,26}^{\circ} + φ)$ möglichst groß ist.

Du weißt, dass der Sinus Werte zwischen $- 1$ und $1$ annimmt. Der größtmögliche Wert des Sinus ist also $1$ .

Dieser Wert wird für den Winkel $90^{\circ}$ angenommen.

Für $90^{\circ} = {60,26}^{\circ} + φ$ folgt $φ = 90^{\circ} - {60,26}^{\circ} = {29,74}^{\circ}$ .

Damit erhältst du

{L P_{n}}_{min} = \frac{5,21}{\sin (90^{\circ})} = \frac{5,21}{1} = 5,21 cm .

Lösung zu Teilaufgabe B 2.4

In dieser Teilaufgabe arbeitest du mit dem Kosinussatz.

Diesen wendest du auf das Dreieck $K L P_{2}$ an. Da die Schenkel $[K L]$ und $[L P_{2}]$ in einem gleichschenkligen Dreieck gleich lang sind, berechnest du:

${K P_{2}}^{2}$	$=$	${L P_{2}}^{2} + {K L}^{2} - 2 \cdot L P_{2} \cdot K L \cdot \cos (∢ K L P_{2})$
	$=$	${K L}^{2} + {K L}^{2} - 2 \cdot {K L}^{2} \cdot \cos (∢ K L P_{2})$
	$=$	$2 \cdot {K L}^{2} - 2 \cdot {K L}^{2} \cdot \cos (∢ K L P_{2})$
	$=$	$2 \cdot {K L}^{2} \cdot (1 - \cos (180 ° - 2 \cdot 60,26 °))$

Dabei hast du die Innenwinkelsumme im Dreieck $K L P_{2}$ verwendet:

∢ K L P_{2} = 180^{\circ} - ∢ L K S - ∢ L K S = 180^{\circ} - 2 \cdot {60,26}^{\circ} .

Setzt du nun $K L = 6 cm$ aus der Aufgabenstellung ein, so erhältst du

K P_{2} = \sqrt{2 \cdot 6^{2} \cdot (1 - \cos (180^{\circ} - 2 \cdot {60,26}^{\circ}))} = 5,95 c m .

Lösungen zu Teilaufgabe B 2.5

Diese Aufgabe benötigt die Flächeninhaltsformel für Trapeze sowie die Volumenformel für Pyramiden.

Erinnere dich zunächst, dass das Volumen einer schiefen Pyramide mit dem einer geraden Pyramide mit gleicher Höhe übereinstimmt. Die Formel lautet daher

V = \frac{1}{3} \cdot G \cdot h .

Dabei bezeichnet $G$ die Grundfläche und $h = P_{n} T_{n}$ die Höhe.

Du benötigst also zunächst die Fläche des Trapezes $A B C D$ . Da $[K L]$ die Höhe des Trapezes ist, kannst du mit der Flächeninhaltsformel den Flächeninhalt der Grundfläche berechnen:

G = \frac{1}{2} \cdot (a + c) \cdot h = \frac{1}{2} (A D + B C) \cdot K L = \frac{1}{2} \cdot (8 + 12) \cdot 6 = 60 c m^{2}

Nun musst du noch die Länge $P_{n} T_{n}$ berechnen. Dazu wendest du die Sinusbeziehung auf das rechtwinklige Dreieck $T_{n} L P_{n}$ an:

P_{n} T_{n} = \sin (φ) \cdot L P_{n} (φ)

Die Länge $L P_{n} (φ)$ kennst du bereits aus Teilaufgabe B 2.3 und kannst daher abschließend alles gesammelt in die Volumenformel der Pyramide einsetzen:

V = \frac{1}{3} \cdot 60 \cdot \sin (φ) \cdot \frac{5,21}{\sin ({60,26}^{\circ} + φ)} = \frac{104,20 \cdot \sin (φ)}{\sin ({60,26}^{\circ} + φ)} {cm}^{3}

Lösung zu Teilaufgabe B 2.6

In dieser Teilaufgabe benötigst du erneut die Volumenformel von Pyramiden sowie die trigonometrischen Beziehungen.

Aus der Aufgabenstellung weißt du, dass die Grundfläche $B C G F$ der Pyramide ein Rechteck ist. Daher gilt für den Flächeninhalt:

G = B C \cdot F G = B C \cdot A E = 12 \cdot 7 = 84 (c m^{2})

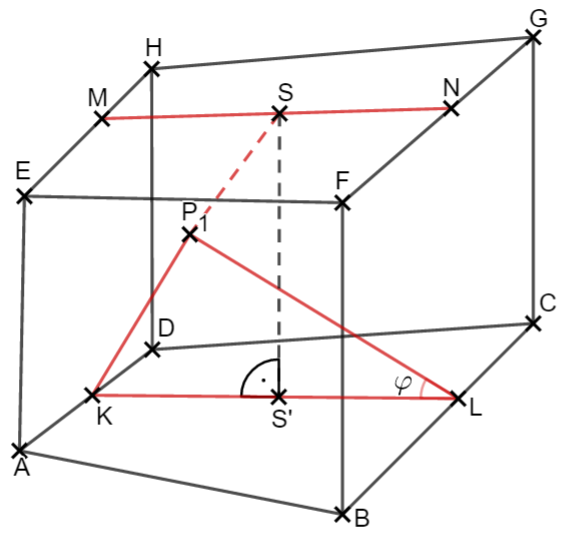
Für die Höhe musst du die Länge der Strecke $[P_{3} U]$ (siehe dazu die rechtsstehende Abbildung) berechnen. Hierbei ist $U$ der Lotfußpunkt von $P_{3}$ auf die Strecke $[N L]$ .

Es gilt $P_{3} U = T_{3} L$ .

Erinnere dich an die Kosinusbeziehung

\cos (φ) = \frac{Ankathete}{Hypotenuse} = \frac{T_{3} L}{L P_{3}} .

Löst du diese nach $T_{3} L$ auf, so erhältst du

T_{3} L = \cos (φ) \cdot L P_{3} .

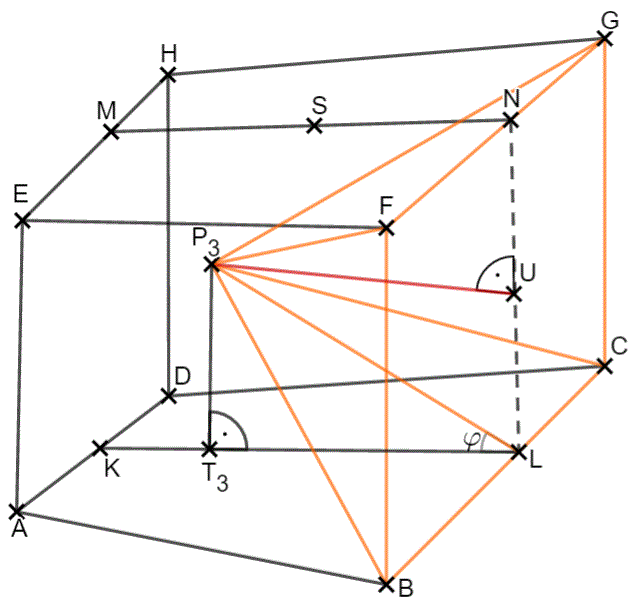
Die Länge $L P_{n}$ hast du bereits in Teilaufgabe B 2.3 für jedes $n$ bestimmt:

L P_{n} (φ) = \frac{5,21}{\sin ({60,26}^{\circ} + φ)} c m .

Diese Beziehung gilt selbstverständlich auch für $n = 3$ und du setzt ein, um

T_{3} L = \cos (φ) \cdot L P_{3} = \cos (φ) \cdot \frac{5,21}{\sin ({60,26}^{\circ} + φ)} cm

zu erhalten.

Mit der Volumenformel für Pyramiden gilt also:

V = \frac{1}{3} \cdot G \cdot h = \frac{1}{3} \cdot G \cdot T_{3} L = \frac{84}{3} \cdot \cos (φ) \cdot \frac{5,21}{\sin ({60,26}^{\circ} + φ)} c m^{3}

Dies setzt du mit dem in Teilaufgabe B 2.5 berechneten Pyramidenvolumen gleich und löst die Gleichung nach $φ$ auf. Dafür benötigst du die Umkehrfunktion des Tangens, den Arcustangens. Um diesen zu verwenden, kannst du die Taste $\tan^{- 1}$ auf deinem Taschenrechner benutzen. Damit erhältst du:

$\frac{84}{3} \cdot \cos (φ) \cdot \frac{5,21}{\sin ({60,26}^{\circ} + φ)}$	$=$	$\frac{104,20 \cdot \sin (φ)}{\sin ({60,26}^{\circ} + φ)}$	$\cdot \sin ({60,26}^{\circ} + φ)$
$\frac{84}{3} \cdot 5,21 \cdot \cos (φ)$	$=$	$104,20 \cdot \sin (φ)$	$: 104,20$
$\frac{84 \cdot 5,21}{3 \cdot 104,20} \cdot \cos (φ)$	$=$	$\sin (φ)$	$: \cos (φ)$
$\frac{84 \cdot 5,21}{3 \cdot 104,20}$	$=$	$\frac{\sin (φ)}{\cos (φ)}$
	↓	Zusammenfassen.
$1,4$	$=$	$\tan (φ)$	$\arctan (\cdot)$
$φ$	$=$	$\arctan (1,4)$
	$=$	$54,46 °$

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?