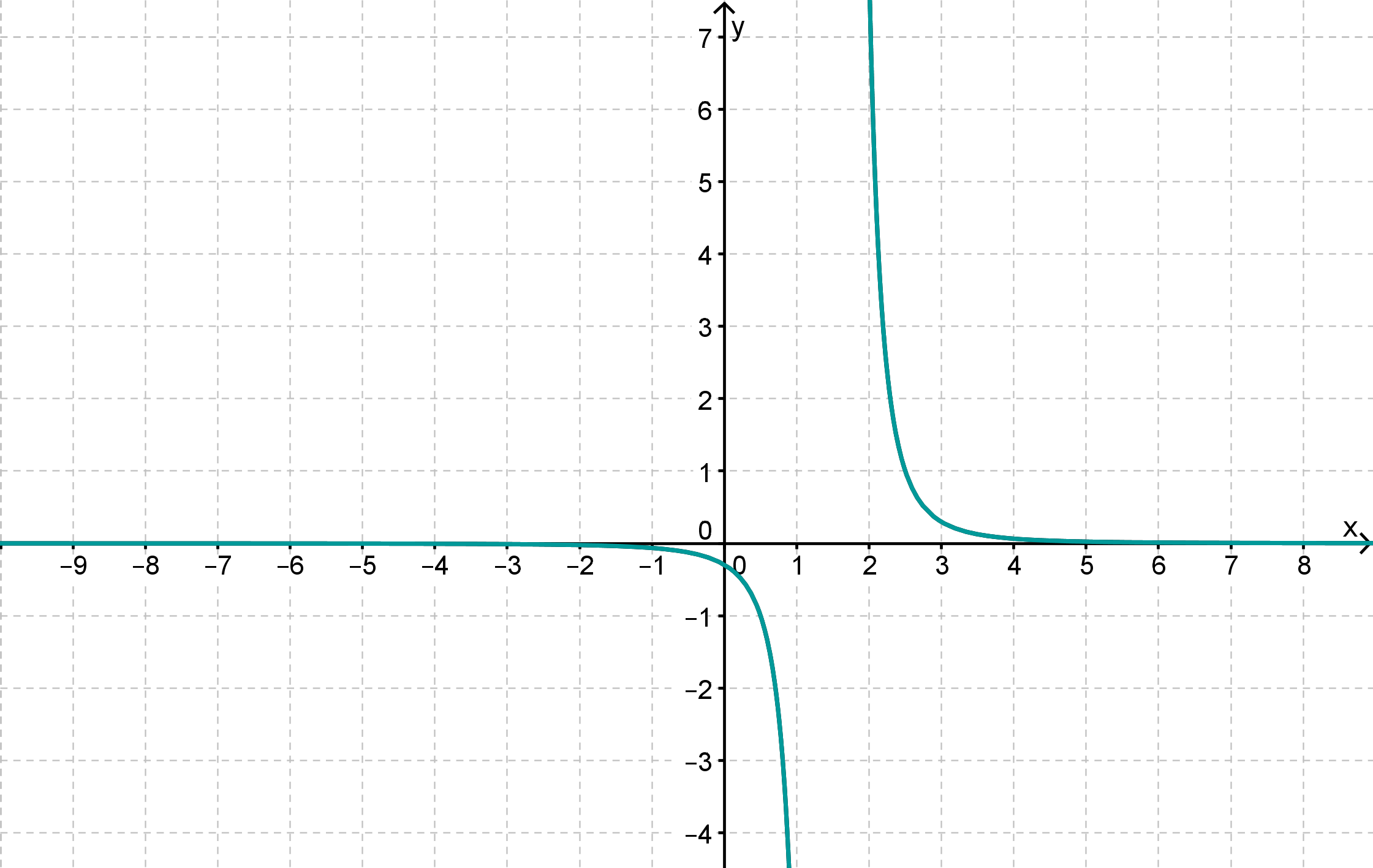
Sieh dir den dargestellten Graphen an: Welchen Wert vermutest du aufgrund der Abbildung für
den Grenzwert für ?
den Grenzwert für ?
den Grenzwert bei Annäherung von links an die Definitionslücke?
den Grenzwert bei Annäherung von rechts an die Definitionslücke?
Bezeichne die Funktion mit und verwende eine korrekte mathematische Schreibweise mit dem Limes (also z. B. bei Teilaufgabe 1 usw.).
(Anmerkung und Hilfe: Die Definitionslücke von ist natürlich bei .)
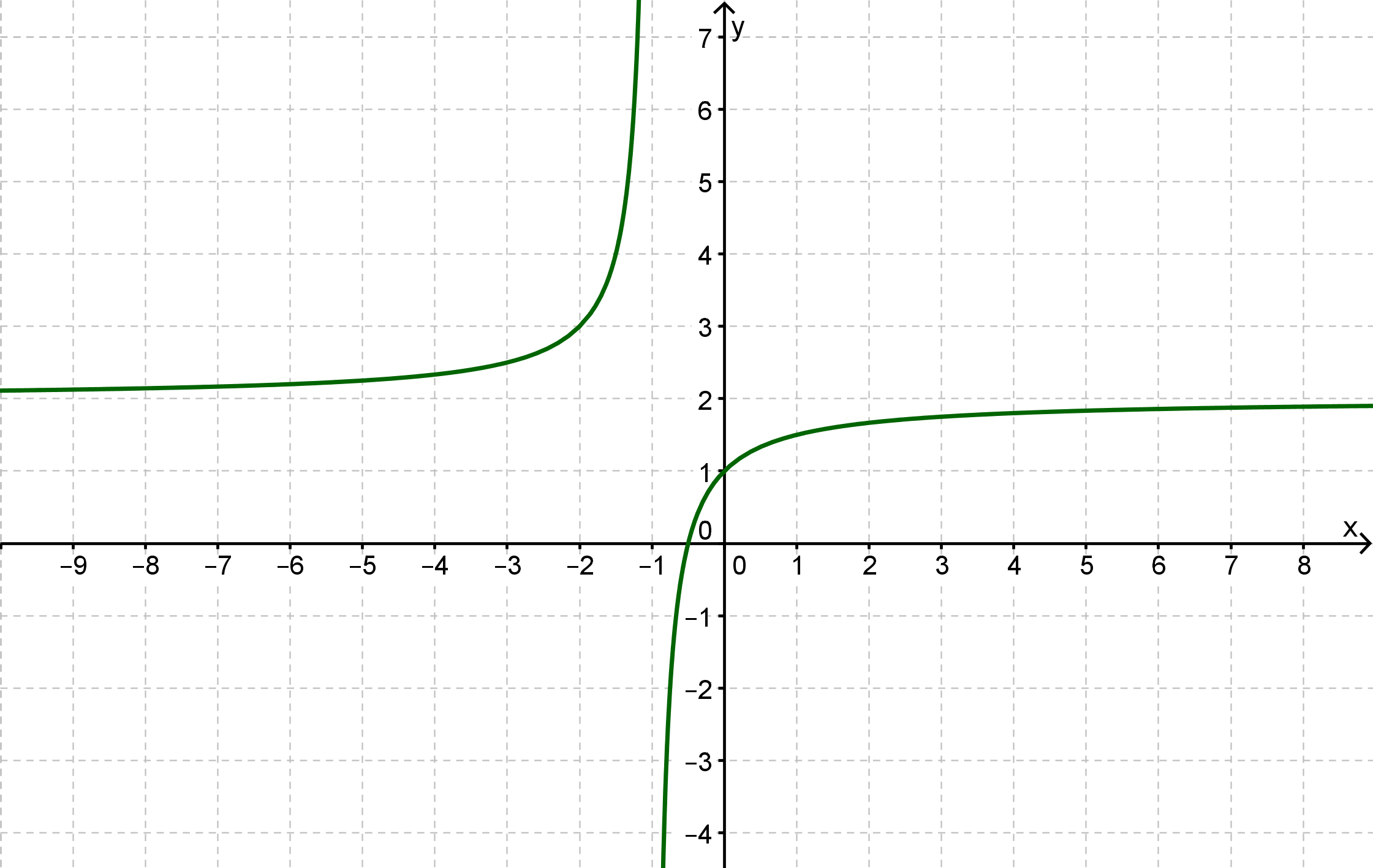
(Anmerkung und Hilfe: Die Definitionslücke von ist natürlich bei .)
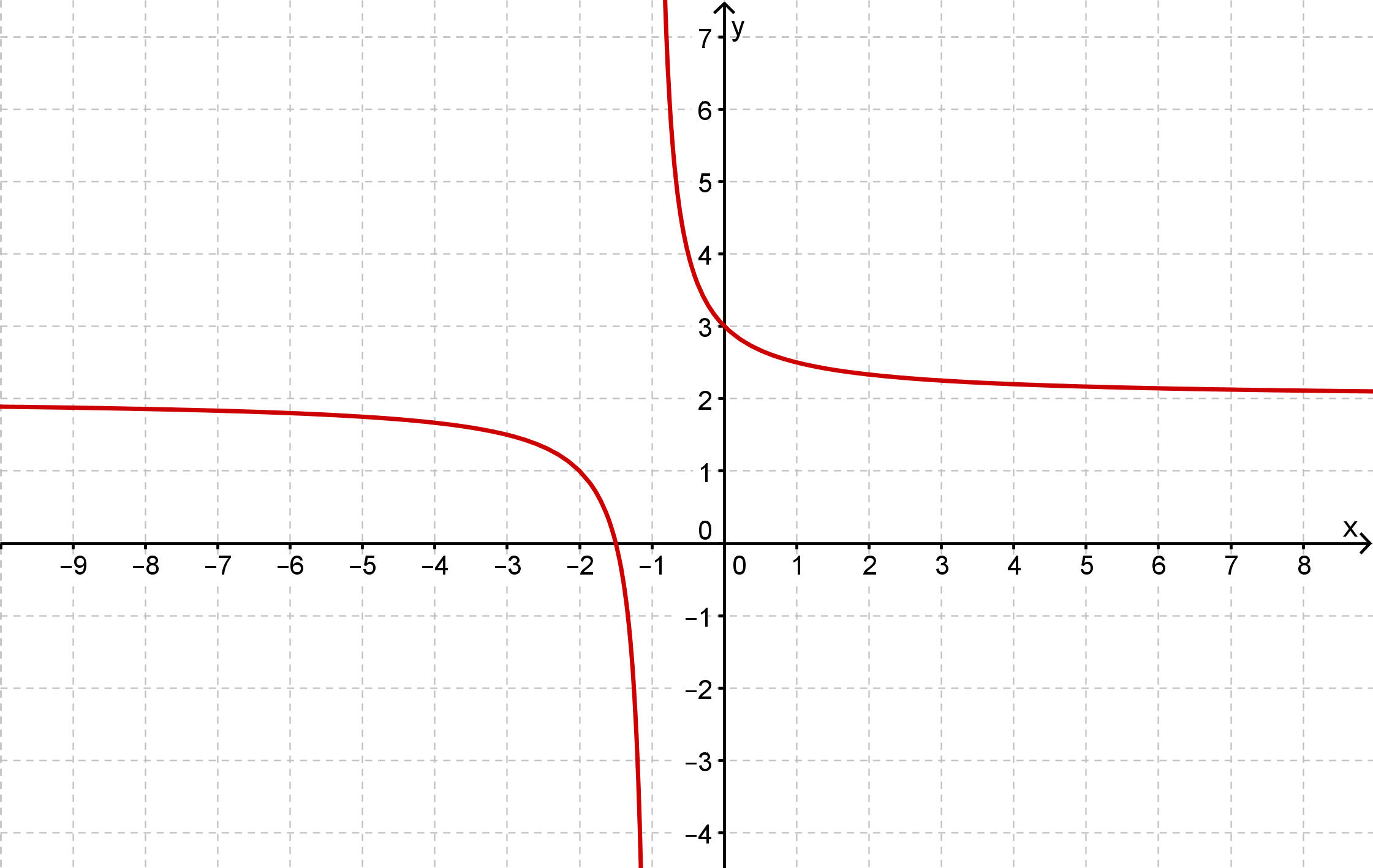
(Anmerkung und Hilfe: Die Definitionslücke von ist bei .)
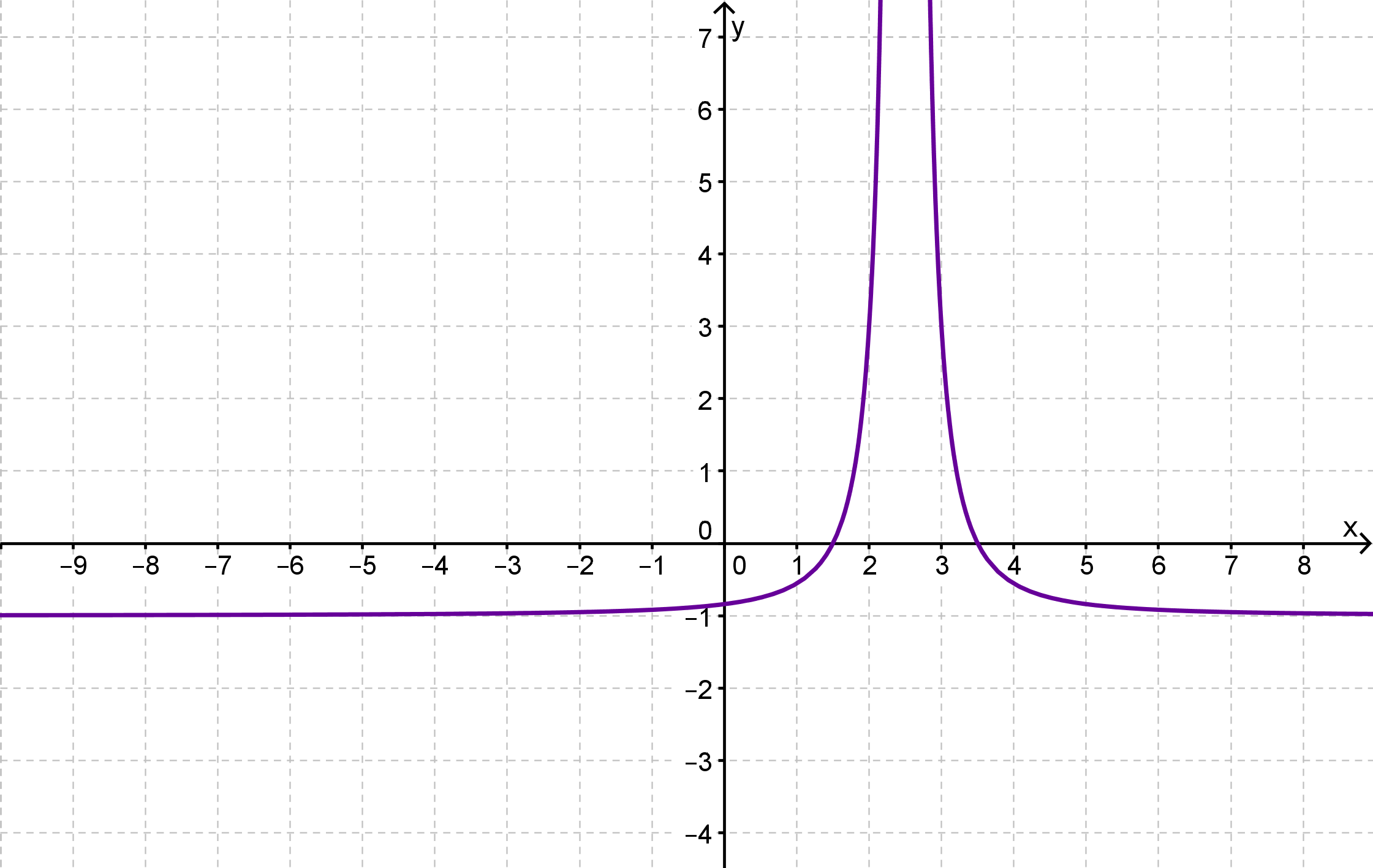
(Anmerkung und Hilfe: Die Definitionslücke von ist natürlich bei .)
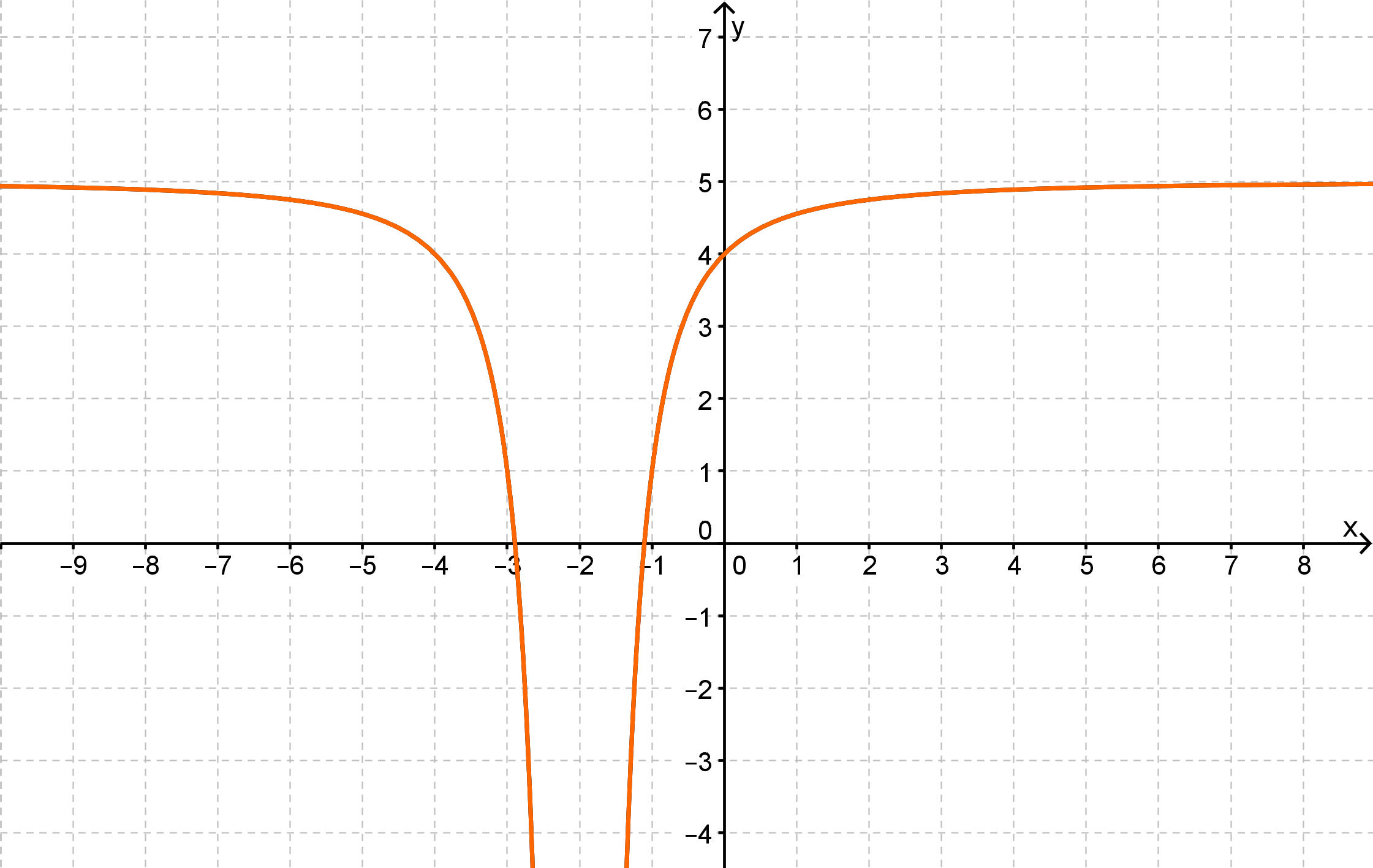
(Anmerkung und Hilfe: Die Definitionslücke von ist bei .)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
