Aufgaben zu Integralen - lernen mit Serlo!

Berechne.

$\int_{-1}^1e^{\left|x\right|}\ \mathrm{d}x$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrieren

$\int_{-1}^1e^{\left|x\right|}\ \mathrm{d}x$

Fallunterscheidung für $x\geq0$ und $x<0$

Für $x\geq0$ ist der Betrag immer positiv und kann weggelassen werden.

Für $x<0$ muss der Betrag durch ein Minuszeichen vor $x$ ersetzt werden, da $-x$ für negatives $x$ positiv wird.

Fall $x\geq0$

$\displaystyle \int_0^1e^x\ \mathrm{d}x$	$=$
	↓	Integrieren.
	$=$	$\displaystyle \left[e^x\right]_0^1$
	↓	In die Klammer wird für $x$ der obere Wert $1$ eingesetzt und minus die Klammer mit dem unteren Wert $0$ gerechnet.
	$=$	$\displaystyle e^1-e^0$
	$=$	$\displaystyle e-1$

Fall $x<0$

$\displaystyle \int_{-1}^0e^{-x}\ \mathrm{d}x$	$=$
	↓	Integrieren.
	$=$	$\displaystyle \left[-e^{-x}\right]_{-1}^0$
	↓	In die Klammer wird für $x$ der obere Wert $0$ eingesetzt und minus die Klammer mit dem unteren Wert $(-1)$ gerechnet.
	$=$	$\displaystyle \left(-e^{-0}\right)-\left(-e^{-\left(-1\right)}\right)$
	↓	Klammern auflösen.
	$=$	$\displaystyle -e^0+e^1$
	$=$	$\displaystyle -1+e$

Gesamtfläche berechnen

$\displaystyle A$	$=$	$\displaystyle \left(e-1\right)+\left(-1+e\right)$
	↓	Klammern auflösen.
	$=$	$\displaystyle e-1-1+e$
	$=$	$\displaystyle 2e-2$

Alternative Lösung

Graph Funktion achsensymmetrisch Integration

Du kannst hier ausnutzen, dass die Funktion achsensymmetrisch ist. Damit ist der Flächeninhalt, der zwischen $-1$ und $0$ eingeschlossen ist, genauso groß wie der Flächeninhalt, der zwischen $0$ und $1$ eingeschlossen ist (siehe Abbildung rechts).

$\Rightarrow$ $\int_{-1}^1e^{\left|x\right|}\ \mathrm{d}x=2 \cdot \int_0^1e^x\ \mathrm{d}x$

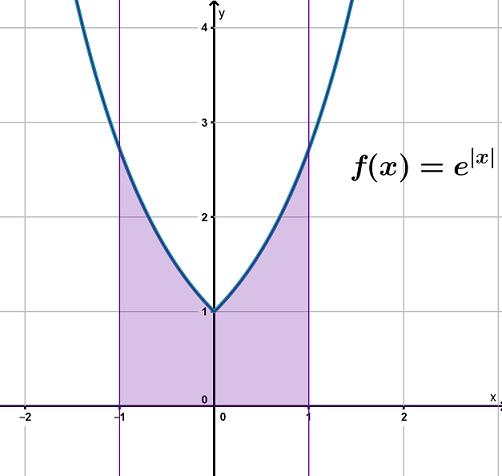
Gleiche Rechnung wie oben.

$=2\cdot\left[e^x\right]_0^1=2\cdot[e^1-e^0]$ $=2\cdot(e-1)=\ 2e-2$

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

$\int_{-2}^0e^{-\left|x\right|}\ \mathrm{d}x$

$\int_{-2}^0e^{\left|x+1\right|}\ \mathrm{d}x$

$\int_{-7}^7\frac{\left|t\right|}te^{\left|t\right|}\ \mathrm{d}t$

Fall $x\geq0$

Fall $x<0$

Gesamtfläche berechnen

Alternative Lösung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Fall $x\geq-1$

Fall $x<-1$

Gesamtfläche berechnen

Hast du eine Frage oder Feedback?

Fall $t\geq0$

Fall $t< 0$

Gesamtfläche berechnen

Hast du eine Frage oder Feedback?

$\displaystyle \int_{-2}^0e^{-\left\|x\right\|}\ \mathrm{d}x$	$=$
	↓	Da $x$ immer negativ ( bzw. 0 ) ist, kann der Betrag durch ein minus ersetzt werden.
	$=$	$\displaystyle \int_{-2}^0e^{-\left(-x\right)}\ \mathrm{d}x$
	$=$	$\displaystyle \int_{-2}^0e^x\ \mathrm{d}x$
	↓	Integrieren.
	$=$	$\displaystyle \left[e^x\right]_{-2}^0$
	↓	In die Klammer wird für $x$ der obere Wert 0 eingesetzt und minus die Klammer mit dem unteren Wert (-2) gerechnet.
	$=$	$\displaystyle e^0-e^{-2}$
	$=$	$\displaystyle 1-\frac{1}{e^2}$
	$≈$	$\displaystyle 0{,}86467$

$\displaystyle \int_{-1}^0e^{x+1}\ \mathrm{d}x$	$=$
	↓	Integrieren.
	$=$	$\displaystyle \left[e^{x+1}\right]_{-1}^0$
	↓	In die Klammer wird für $x$ der obere Wert $0$ eingesetzt und minus die Klammer mit dem unteren Wert $-1$ gerechnet.
	$=$	$\displaystyle e^1-e^0$
	$=$	$\displaystyle e-1$

$\displaystyle \int_{-2}^{-1}e^{-\left(x+1\right)}\ \mathrm{d}x$	$=$
	↓	Klammern auflösen.
	$=$	$\displaystyle \int_{-2}^{-1}e^{-x-1}\ \mathrm{d}x$
	↓	Integrieren.
	$=$	$\displaystyle \left[-e^{-x-1}\right]_{-2}^{-1}$
	↓	In die Klammer wird für $x$ der obere Wert $-1$ eingesetzt und minus die Klammer mit dem unteren Wert $-2$ gerechnet.
	$=$	$\displaystyle (-e^{-(-1)-1})-(-e^{-(-2)-1})$
	↓	Klammern auflösen.
	$=$	$\displaystyle -e^0+e^1$
	$=$	$\displaystyle -1+e$

$\displaystyle \int_0^7\frac{t}{t}e^t\ \mathrm{d}t$	$=$
	↓	Mit t kürzen.
	$=$	$\displaystyle \int_0^7e^t\ \mathrm{d}t$
	↓	Integrieren.
	$=$	$\displaystyle \left[e^t\right]_0^7$
	↓	In die Klammer wird für tt der obere Wert (7) eingesetzt und minus die Klammer mit dem unteren Wert (0) gerechnet.
	$=$	$\displaystyle e^7-e^0$
	$=$	$\displaystyle e^7-1$

$\displaystyle \int_{-7}^0\frac{-t}{t}e^{-t}\ \mathrm{d}t$	$=$
	↓	Mit t kürzen.
	$=$	$\displaystyle \int_{-7}^0-e^{-t}\ \mathrm{d}t$
	↓	Integrieren.
	$=$	$\displaystyle \left[e^{-t}\right]_{-7}^0$
	↓	In die Klammer wird für $t$ der obere Wert (0) eingesetzt und minus die Klammer mit dem unteren Wert (-7) gerechnet.
	$=$	$\displaystyle e^0-e^{-\left(-7\right)}$
	$=$	$\displaystyle 1-e^7$

$\displaystyle A$	$=$	$\displaystyle \left(e^7-1\right)+\left(1-e^7\right)$
	$=$	$\displaystyle e^7-1+1-e^7$
	$=$	$\displaystyle 0$

Fall x≥0x\geq0x≥0

Fall x<0x<0x<0

Gesamtfläche berechnen

Alternative Lösung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Fall x≥−1x\geq-1x≥−1

Fall x<−1x<-1x<−1

Gesamtfläche berechnen

Hast du eine Frage oder Feedback?

Fall t≥0t\geq0t≥0

Fall t<0t< 0t<0

Gesamtfläche berechnen

Hast du eine Frage oder Feedback?

Fall $x\geq0$

Fall $x<0$

Fall $x\geq-1$

Fall $x<-1$

Fall $t\geq0$

Fall $t< 0$