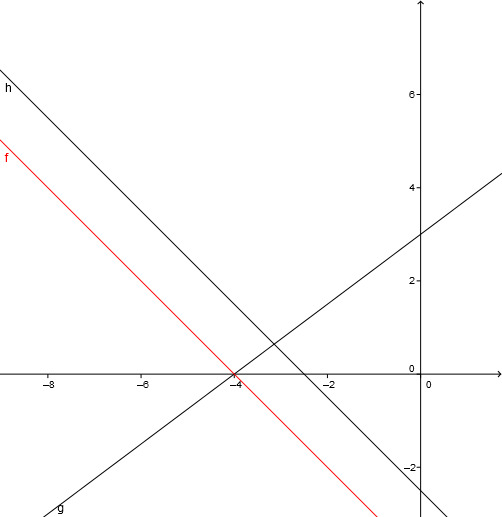
Gegeben sind die Funktionen und .
Die Gerade h soll so in y-Richtung verschoben werden, dass g und die verschobene Gerade h die x-Achse im gleichen Punkt schneiden.
Bestimmen Sie den Funktionsterm für die verschobene Gerade.
ist der Funktionsterm der Geraden.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann → Was bedeutet das?