Weitere Aufgaben zu linearen Funktionen
Hier findest du gemischte Übungsaufgaben zu linearen Funktionen. Schaffst du sie alle?
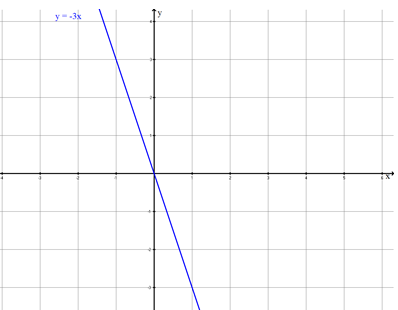
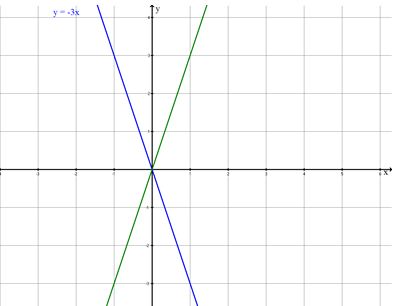
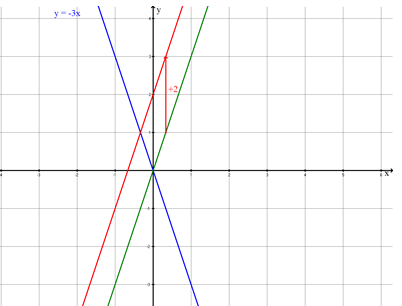
- 1
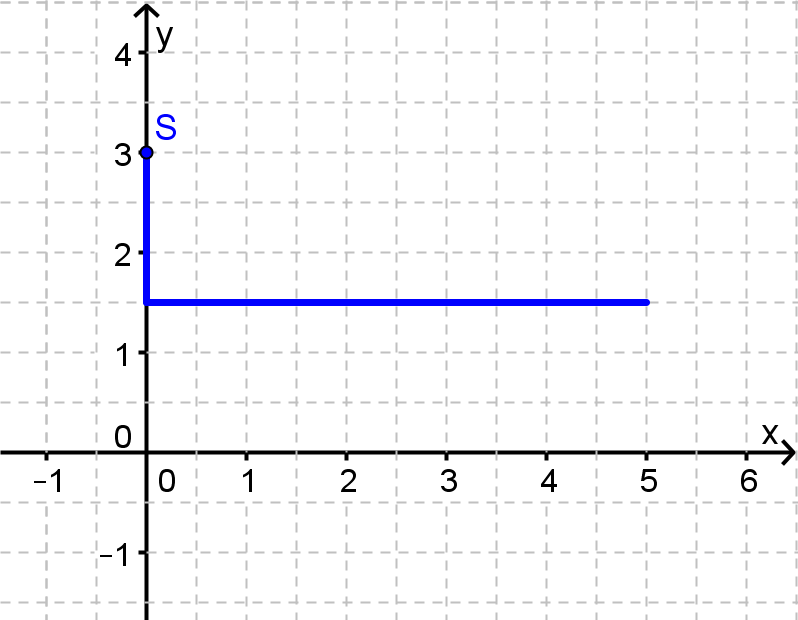
Die Gerade wird an der -Achse gespiegelt.
Die gespiegelte Gerade wird anschließend um 2 Einheiten nach oben verschoben.
Bestimme die Gleichung der neuen Geraden zeichnerisch und rechnerisch.
ist die Gleichung der Geraden. - 2
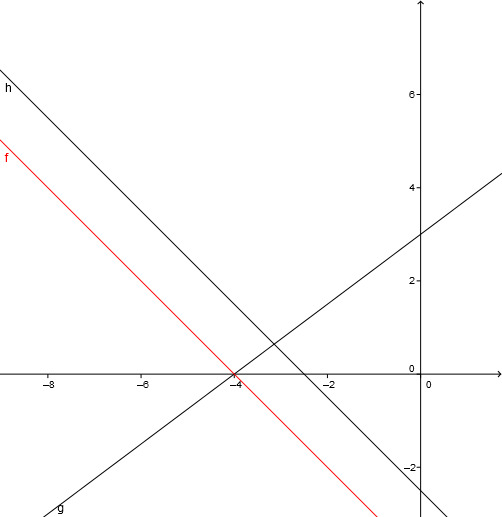
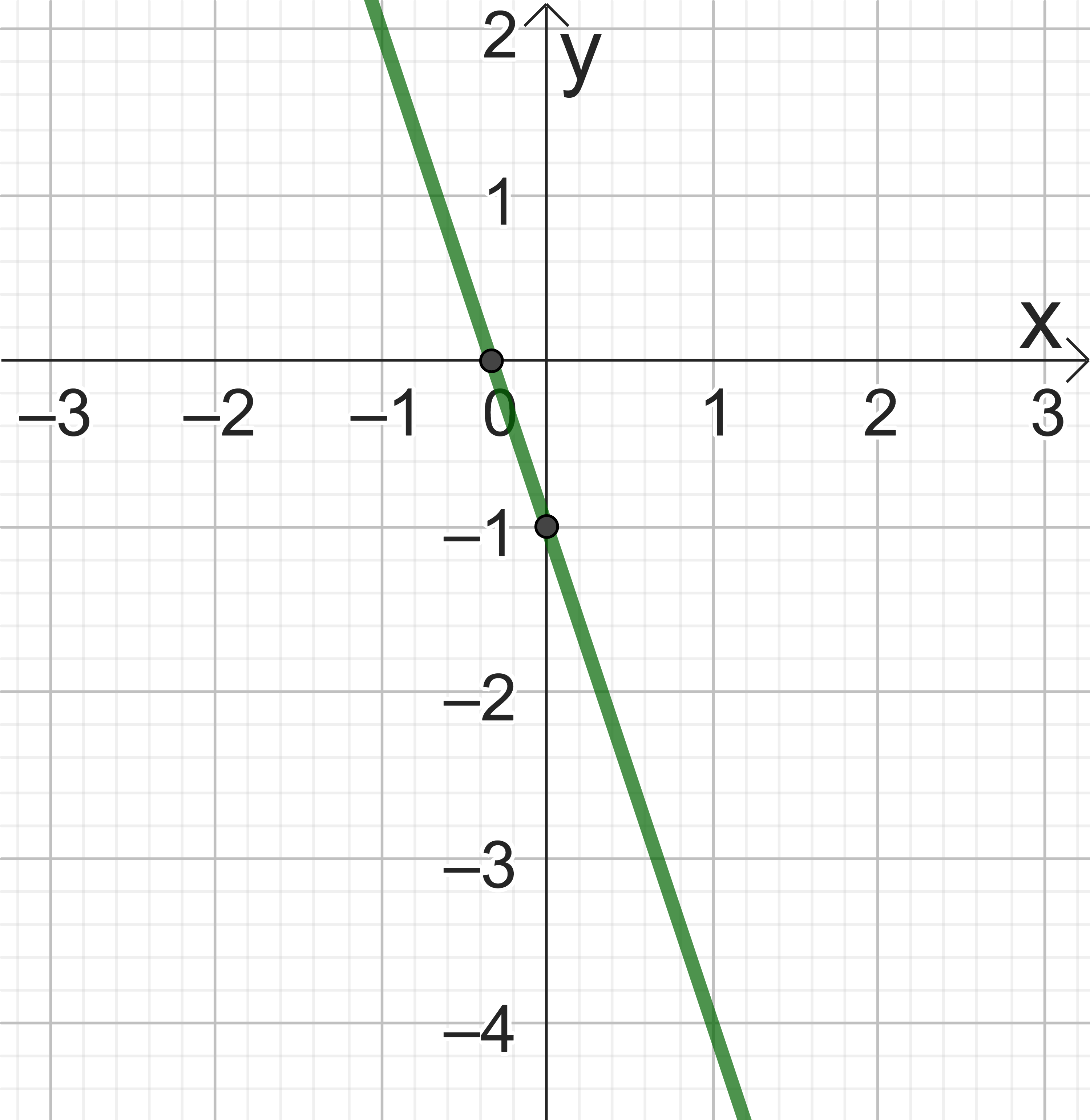
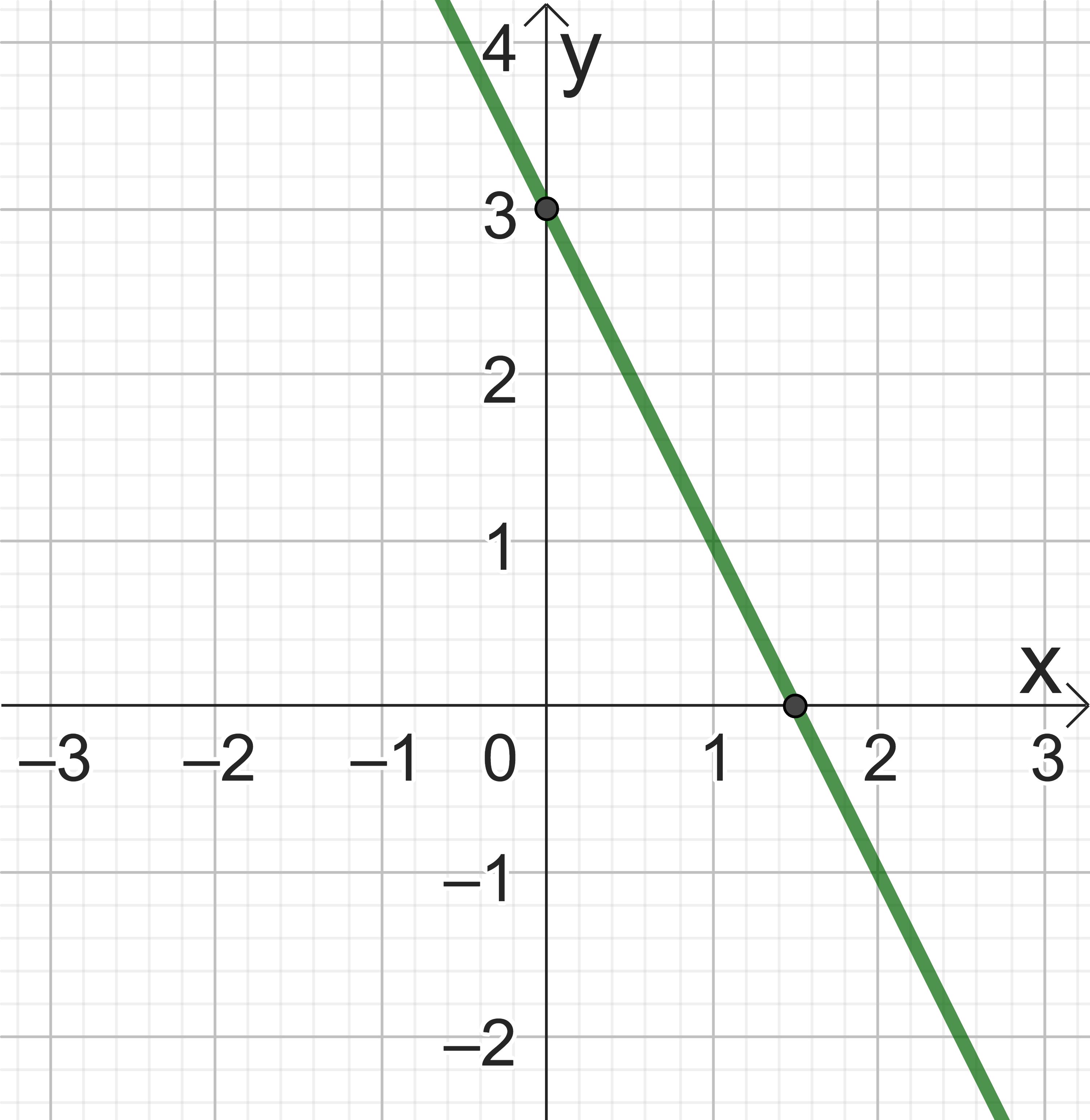
Gegeben sind die Funktionen und .
Die Gerade h soll so in y-Richtung verschoben werden, dass g und die verschobene Gerade h die x-Achse im gleichen Punkt schneiden.
Bestimmen Sie den Funktionsterm für die verschobene Gerade.
ist der Funktionsterm der Geraden. - 3
Gegeben ist der Punkt mit
Wählen Sie für t einige Werte und tragen Sie die dazugehörigen Punkte in ein Koordinatensystem ein.
Wie liegen die Punkte im Koordinatensystem? Für welche t- Werte gilt: x- Koordinate ist gleich y- Koordinate des Punktes P?
- 4
Zeigen Sie: Die Gerade g durch und besitzt die Steigung und schneidet die y-Achse in
- 5
Zeigen Sie: Die Punkte liegen für alle auf einer Geraden.
Bestimmen Sie die Geradengleichung.
- 6
Ermitteln Sie den Funktionsterm der linearen Funktion , wenn gilt:
- 7
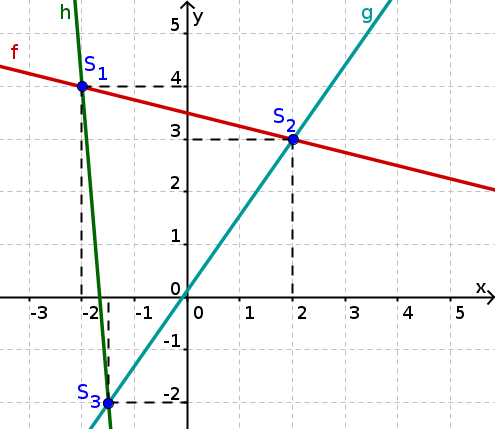
Bestimmung von Schnittpunkten
Im Koordinatensystem sind drei Geraden eingezeichnet. Lies die Schnittpunkte aus der Abbildung ab und gib sie nacheinander in das Eingabefeld ein.
Punkte können in dieser Form eingegeben werden: "(-2|0,5)"
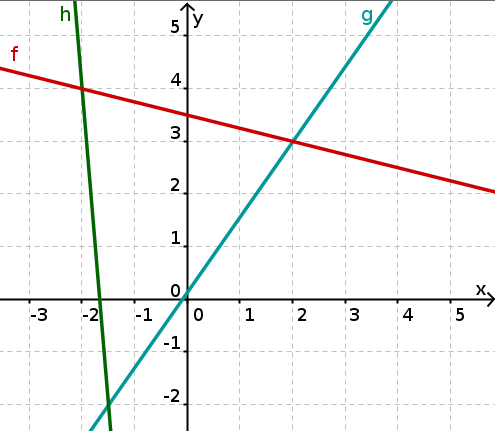
- 8
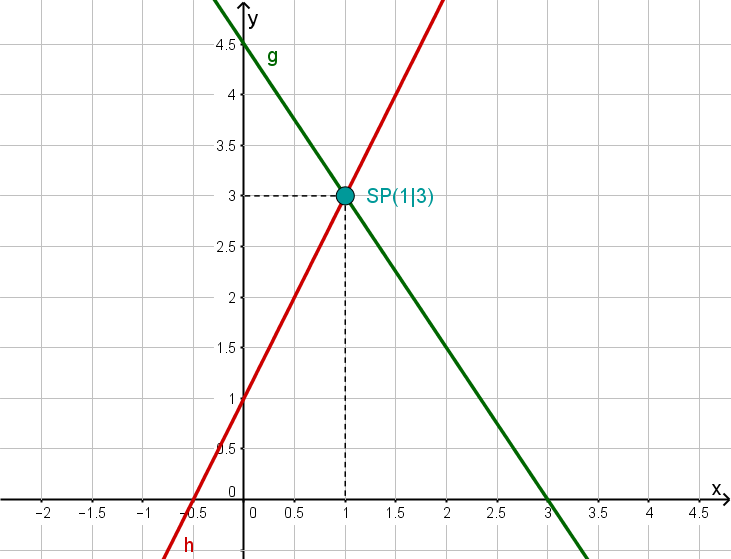
Bestimmung von Schnittpunkten
Gegeben ist eine Gerade g und eine Gerade h.
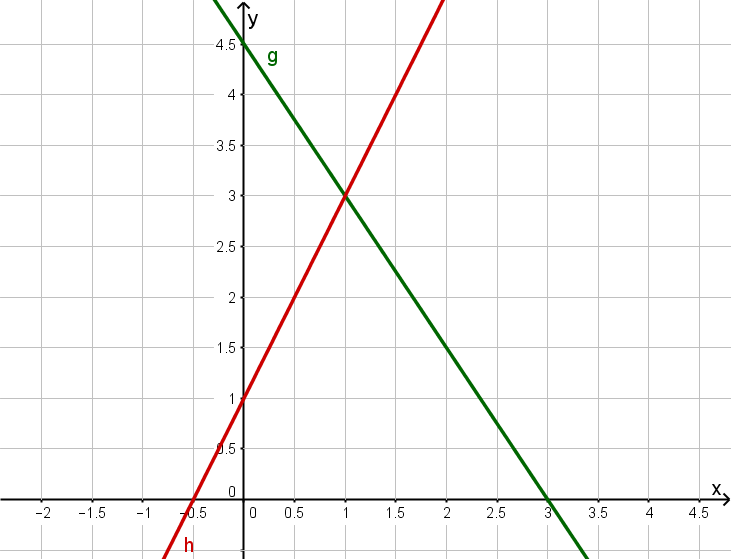
Bestimme die Geradengleichungen von g und h.
Lies den Schnittpunkt ab.
Gib den Punkt in das Eingabefeld ein. Beispiel: "(-2;1)" oder "(-2|1)"
- 9
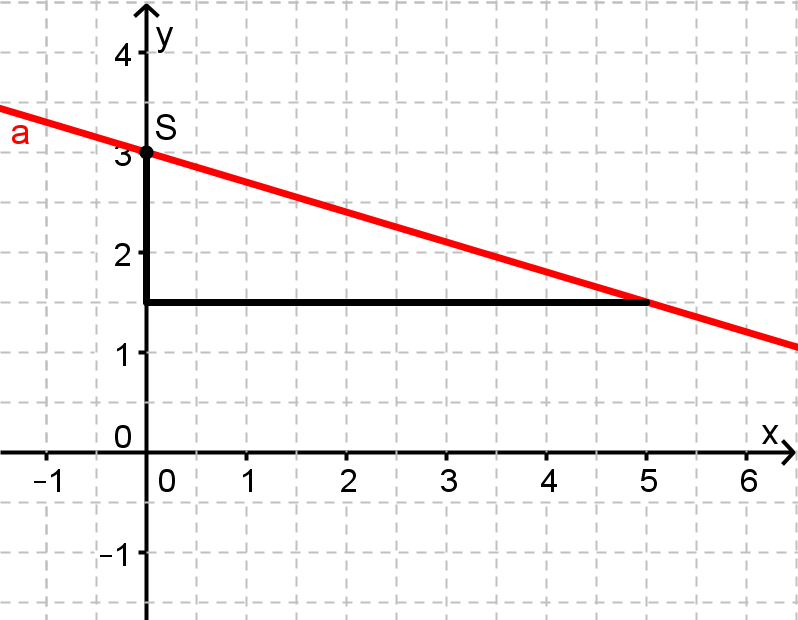
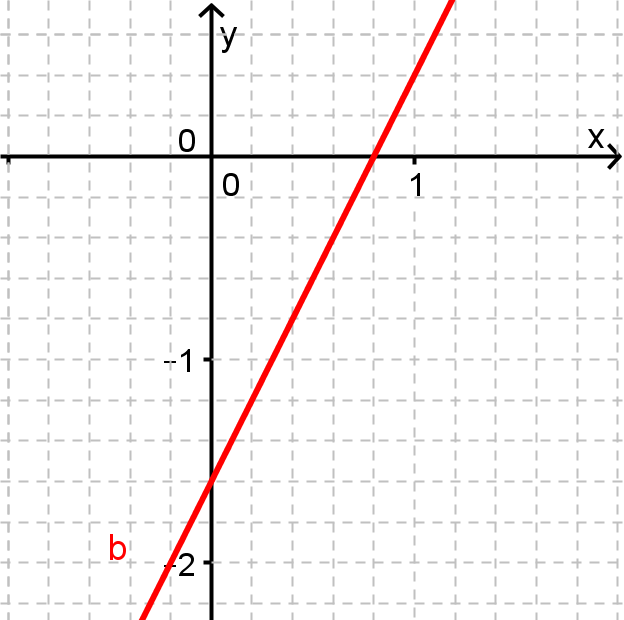
Gegeben ist die Funktion
Gib den Schnittpunkt mit der y-Achse an ohne zu rechnen.
Form: (x;y)Gib die Wertemenge der Funktion an wenn gilt: , es sich also um die maximal mögliche Definitionsmenge handelt.
Zeichne den Graph der Funktion in ein Koordinatensystem mit geeigneten Abmessungen.
Gib den Term einer Geraden u an, die parallel zu a ist und durch P(0|-5) verläuft.
Gib die Gleichung einer Geraden v an, die orthogonal zu a ist und durch Q(2|3) verläuft
Bestimme die Nullstelle der Funktion a.
Bestimme den Funktionswert an der Stelle x=0,23
Entscheide durch Rechnung, ob der Punkt R(-0,5|3) über, unter oder auf dem Graphen von a liegt.
Bestimme rechnerisch den Schnittpunkt der dargestellten Gerade b mit der Gerade a, indem du zuvor den Term aus dem Koordinatensystem abliest.
Gib den Punkt in das Eingabefeld ein. Beispiel: "(-2;1)" oder "(-2|1)"
- 10
Wissensquiz lineare Funktionen 1
- 11
Wissensquiz lineare Funktionen 2
- 12
Wissensquiz lineare Funktionen 3
- 13
Ordne jeweils richtig zu:
Funktionsgleichung
y-Achsenschnittpunkt
x-Achsenschnittpunkt
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?