Funktionenschar

Bei einer Funktionenschar gibt es neben der Variable $x$ auch noch einen Parameter (häufig $a$ oder $k$ ), welchen man frei auf eine Zahl festlegen kann. Für jede Besetzung des Parameters bekommt man einen anderen Funktionsterm und somit auch einen anderen Funktionsgraphen.

Repräsentanten der Funktionenschar

Möchte man Repräsentanten der Schar zu bestimmten Parameterwerten zeichnen oder damit rechnen, so setzt man für den Parameter Werte ein und erhält eine Funktion der Funktionenschar.

Beispiel

Betrachte die Funktionen $f_k(x)=k\cdot x$ .

Für $k=2$ ist $f_2(x)=2\cdot x$ . Der Graph von $f_2(x)$ ist eine Gerade durch den Ursprung mit Steigung $2$ .

Setze weitere Werte für k ein, um weitere Funktionen zu bestimmen. Die entstandenen Funktionen sind Teil der Funktionenschar $f_k(x)$ .

$k$	$f_k(x)$
$1$	$f_1(x)=1\cdot x$
$2$	$f_2(x)=2\cdot x$
$4$	$f_4(x)=4\cdot x$
$0{,}5$	$f_{0{,}5}(x)=0{,}5\cdot x$
$-2$	$f_{-2}(x)=-2\cdot x$
$-0{,}5$	$f_{-0{,}5}(x)=-0{,}5\cdot x$
$-7$	$f_{-7}(x)=-7\cdot x$

Die Funktionen lassen sich dann in einem Koordinatensystem zeichnen.

Weitere Beispiele

$f_k(x)= \frac 1 2 x^3-kx^2-k^2$ liefert zum Beispiel

für $k=3$ die Funktion $f_3(x)=\frac{1}{2}x^3-3x^2-9$
für $k=-2$ die Funktion $f_{-2}(x)=\frac 1 2 x^3+2x^2-4$ .

Die entstandenen Funktionen kannst du wieder wie gewohnt untersuchen und zeichnen.

In Abhängigkeit vom Parameter

Häufig untersuchst du die Funktionenschar allerdings in Abhängigkeit von $k$ . Doch was bedeutet das eigentlich?

Nun, das heißt, dass das Ergebnis davon abhängt, welcher Wert des Parameters eingesetzt wird. Wie das konkret ausschauen kann, siehst du gleich in dem Beispiel weiter unten. Eine schöne Übersicht über Sachen, die man in Abhängigkeit von einem Parameter berechnen kann, findest du auch im Artikel Kurvendiskussion mit Parameter.

Beispiel: Nullstellenberechnung mit Parameter

Willst du die Nullstellen der Funktion $f_a(x)=x^2-a$ berechnen, so gehst du genau so vor, wie du es auch ohne Parameter tun würdest:

$\displaystyle x^2-a$	$=$	$\displaystyle 0$	$\displaystyle +a$
	↓	Löse nach $x$ auf.
$\displaystyle x^2$	$=$	$\displaystyle a$	$\displaystyle \sqrt{ }$
	↓	Ziehe die Wurzel.
$\displaystyle x$	$=$	$\displaystyle \pm\sqrt{a}$

Die Nullstellen liegen bei $x_1=\sqrt a$ und $x_2=-\sqrt a$ .

Für $a=4$ also zum Beispiel bei $x_1=2$ und $x_2=-2$ .

Graphische Beispiele

In diesen Beispielen siehst du, wie Funktionenscharen graphisch aussehen können. Beachte, dass es unendlich viele Repräsentanten einer Funktionenschar, also unendlich viele Funktionen gibt und man nie alle zeichnen kann.

Beispiel 1

${\mathrm f}_\mathrm k(\mathrm x)=\mathrm x+\mathrm k$

$k$ verändert hier den y-Achsenabschnitt, die Funktionen der Schar sind also nach oben oder unten verschoben.

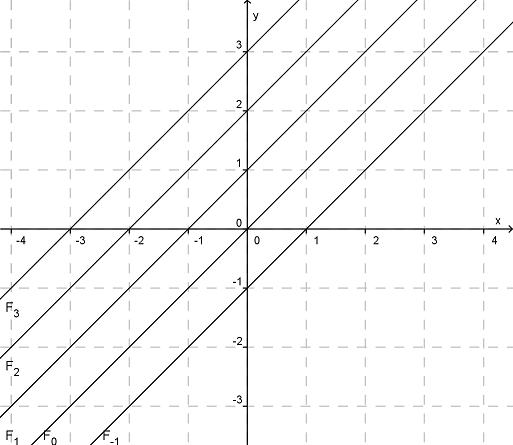
abgebildet sind hier $f_{-1}, f_0, f_1, f_2, f_3$ .

Beispiel 2

${\mathrm f}_\mathrm k(\mathrm x)=\frac{\mathrm k}2\mathrm x+3+\frac{\mathrm k}2$

Gehen alle Funktionen einer Schar durch einen Punkt, so ist dieser ein gemeinsamer Punkt der Funktionenschar.

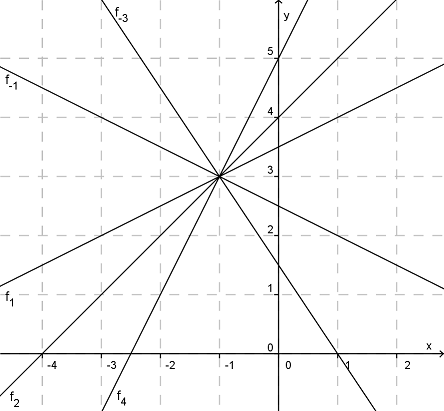
abgebildet sind hier $f_{-3},f_{-1}, f_1, f_2, f_4$ .

Veranschaulichung durch Applet

${\mathrm f}_\mathrm k(\mathrm x)=\mathrm x^3-\frac12\mathrm k^2\mathrm x$

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/1571459]

Verändert man das $k$ an dem Schieberegler, dann verändert sich die schwarze Kurve entsprechend dem Parameter $k$ .

Weiteres Beispiel als Ausblick

${\mathrm f}_\mathrm w(\mathrm x)=\tan\left(-\frac w2\right)(x-\cos(w))+\sin(w)$

Geogebra File: https://assets.serlo.org/legacy/1698.xml

Eine solche Funktionenschar wird höchstwahrscheinlich nicht Gegenstand in der Schule sein, hat aber ästhetischen Wert.

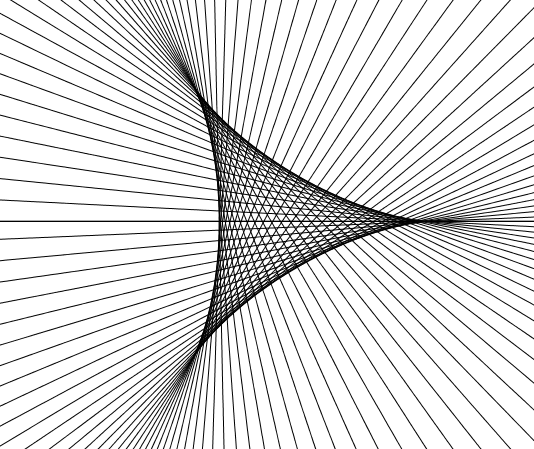
Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?