Eine Spiegelung an den Koordinatenachsen erreicht man durch eine Multiplikation mit an der geeigneten Stelle:
Für die Spiegelung an der -Achse muss der Funktionsterm mit multipliziert werden.
Für die Spiegelung an der -Achse muss das Argument mit multipliziert werden.
Die Umkehrfunktion ist stets eine Spiegelung des Funktionsgraphen an der Winkelhalbierenden des 1. und 3. Quadranten.
Allgemeine Vorgehensweise als Tabelle
Spiegelung ... | Vorgehen | neuer Funktionsterm |
|---|---|---|
... an der x-Achse | Multiplikation mit | |
... an der y-Achse | durch ersetzen | |
... am Ursprung | erst an der x-Achse und dann an der y-Achse spiegeln | |
... an der Winkelhalbierenden des 1. und 3. Quadranten | Der gespiegelte Graph ist die Umkehrfunktion. |
Beispiel
Funktionsterm | Graph | |
|---|---|---|
ursrpüngliche Funktion | 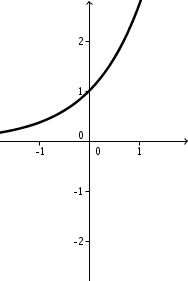 | |
Spiegelung an der x-Achse |  | |
Spiegelung an der y-Achse | 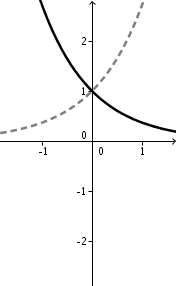 | |
Spiegelung an der Winkelhalbierenden |  |
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
