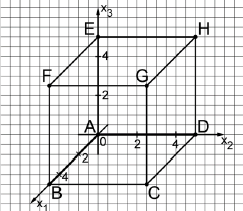
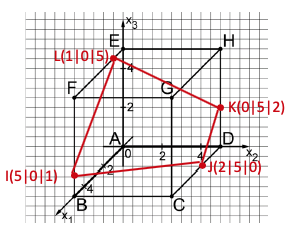
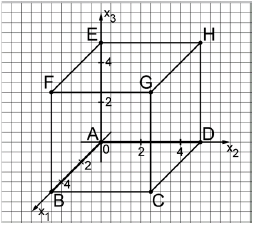
Die Abbildung zeigt den Würfel mit und in einem kartesischen Koordinatensystem. Die Ebene schneidet die Kanten des Würfels unter anderem in den Punkten , , und .
Teilaufgabe a)
(4 BE)
Zeichnen Sie das Viereck in die Abbildung ein und zeigen Sie, dass es sich um ein Trapez handelt, bei dem zwei gegenüberliegende Seiten gleich lang sind.
Teilaufgabe b)
(3 BE)
Ermitteln Sie eine Gleichung der Ebene in Normalenform.
(zur Kontrolle: )
Für ist die Gerade : mit gegeben.
Teilaufgabe c)
(3 BE)
Bestimmen Sie den Wert von so, dass die Gerade die Würfelfläche in ihrem Mittelpunkt schneidet.
Für jedes liegt die Gerade in der Ebene mit der Gleichung .
Teilaufgabe d)
(2 BE)
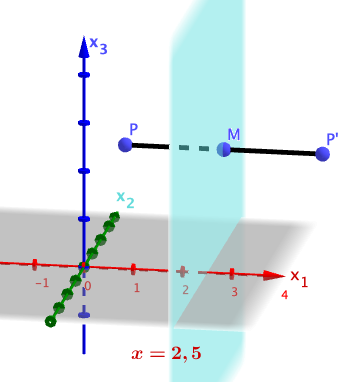
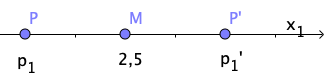
Ein beliebiger Punkt des Raums wird an der Ebene gespiegelt. Geben Sie die Koordinaten des Bildpunkts in Abhängigkeit von , und an.
Teilaufgabe e)
(4 BE)
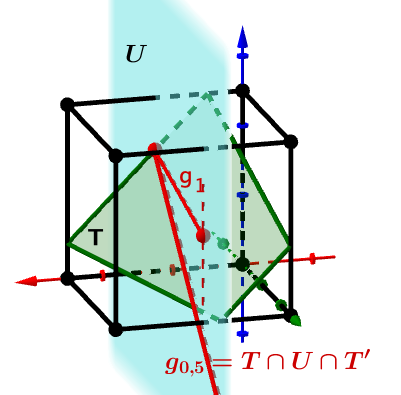
Spiegelt man die Ebene an , so erhält man die von verschiedene Ebene . Zeigen Sie, dass für einen bestimmten Wert von die Gerade in der Ebene liegt, und begründen Sie, dass diese Gerade die Schnittgerade von und ist.
Teilaufgabe f)
(4 BE)
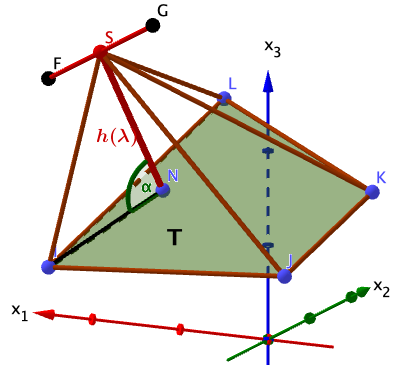
Die Spitze einer Pyramide mit der Grundfläche liegt auf der Kante . Untersuchen Sie, ob die Höhe dieser Pyramide betragen kann.