Aufgaben zu Termen mit Variablen in Sachzusammenhängen
- 1
Gegeben ist ein Quadrat mit der Seitenlänge . Bestimme den Term für den Flächeninhalt des Dreiecks .

- 2
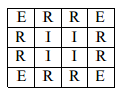
Beim Zerschneiden einer rechteckigen Pizza in waagrechte und senkrechte Streifen entstehen
Eckstücke (E),
reine Randstücke (R)
und Innenstücke (I),
siehe Abbildung für .
Stelle Terme auf, die die Zahl der Randstücke bzw. die Zahl der Innenstücke in Abhängigkeit von der Streifenzahl beschreiben.
- 3
In das Quadrat ist ein grau gefärbter "Doppelpfeil" eingezeichnet.
Gib den Flächeninhalt des Doppelpfeils in Abhängigkeit von und an.
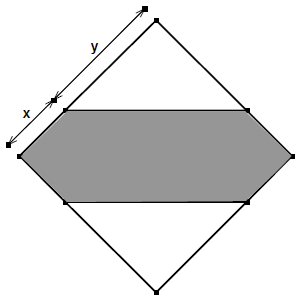
- 4
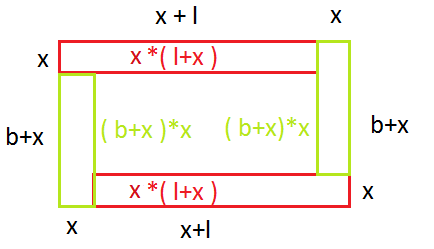
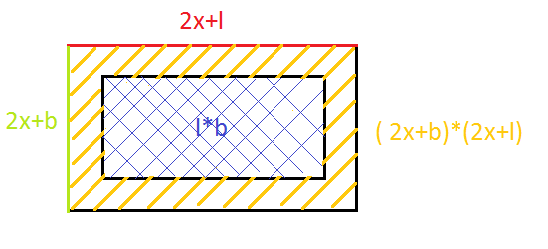
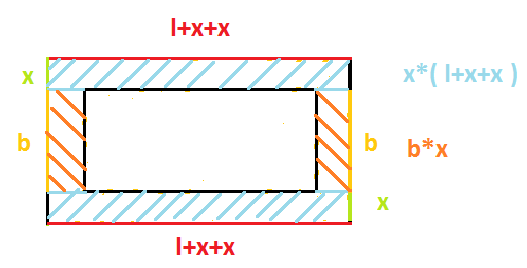
Der Spielfeldrand eines Fußballfeldes der Breite und Länge soll von den Zuschauern den Abstand haben.
Christian, Monika und Peter schreiben Terme auf, die den Flächeninhalt der Sicherheitszone beschreiben:
Christian:
Monika:
Peter:
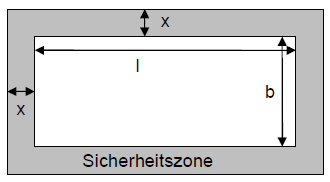
Beschreibe – gegebenenfalls mit Hilfe einer Skizze – wie die drei jeweils ihren Term gefunden haben könnten.
Zeige, dass die Terme äquivalent sind.
Klaus stellt den Term auf und behauptet, dass dieser auch den Flächeninhalt der Sicherheitszone beschreibt. Was meinst du dazu?
In der Münchner Allianz-Arena ist das Spielfeld lang und breit. Der Sicherheitsabstand beträgt . Welchen Flächeninhalt hat die Sicherheitszone?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?