Aufgaben zum Ordnen von Dezimalbrüchen

1
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Erkläre (z. B. durch Einzeichnen auf einer Stellenwerttafel), warum $2,7$ größer als $2,08$ ist.
Welche Zahl liegt in der Mitte dieser beiden Zahlen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stellenwerttafel
Trage die Zahl $2,7$ in die Stellenwerttafel ein:
T
H
Z
E
,
z
h
t
0
0
0
2
,
7
0
0
Vergleiche dies mit der Zahl $2,08$ auf der Stellenwerttafel:
T
H
Z
E
,
z
h
t
0
0
0
2
,
0
8
0
Die beiden Zahlen haben den gleichen Eintrag an der Einerstelle, aber an der Zehntelstelle hat $2,7$ eine $7$ und $2,08$ eine $0$ . Weil $7$ größer als $0$ ist ist $2,7$ größer als 2,08.
Die Differenz der beiden Zahlen beträgt $0,62$ . Die Hälfte von $0,62$ ist $0,31$ . Also liegt die Mitte zwischen den beiden Zahlen bei $2,08 + 0,31 = 2,39$ .
2
Trage in die Stellenwerttafel ein.
1. $0,75$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stellenwerttafel
  T
  H
  Z
  E
  ,
  z
  h
  t
  0
  ,
  7
  5
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $12,598$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stellenwerttafel
  T
  H
  Z
  E
  ,
  z
  h
  t
  1
  2
  ,
  5
  9
  8
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $0,005$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stellenwerttafel
  T
  H
  Z
  E
  ,
  z
  h
  t
  0
  ,
  0
  0
  5
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Vergleiche die Dezimalbrüche und gib an, ob der erste ( $>$ ) oder der zweite ( $<$ ) Bruch größer ist oder ob beide gleich groß sind ( $=$ ).
1. 3,60 und 3,61
  $>$
  $<$
  $=$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vergleich von Dezimalzahlen
  
  Gliedere die Zahl nach Einern (E), Zehnteln (z) und Hundertsteln (h) auf.
  3,60: 3 E 6 z 0 h 3,61: 3 E 6 z 1 h
  Vergleiche zuerst die natürlichenZahlen vor dem Komma.
  3 E = 3 E
  Beide Zahlen vor dem Komma sind gleich groß.
  Vergleiche auch die Zehntel.
  6 z = 6 z
  Beide Zehntel sind gleich groß.
  Vergleiche nun die Hundertstel.
  0 h < 1 h
  Da 0 < 1 ist, ist somit der Dezimalbruch 3,60 kleiner als 3,61.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Vergewissere dich, ob die Zahlen vor dem Komma gleich sind (wie 5,3 und 5,23). Danach vergleichst du die Zahlen nach dem Komma (also 5,3 und 5,23).
  Wichtig:
  5,3 hat denselben Wert wie 5,30 (die 3 ist also eine 30 und keine wortwörtliche 3 - nicht 5,03!).
2. 0,5 und 0,23
  >
  <
  $=$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vergleichen von Dezimalzahlen
  Gliedere Zahl nach Einern (E), Zehnteln (z) und Hundertsteln (h) auf.
  0,5: 0 E 5 z 0 h 0,23: 0 E 2 z 3 h
  Vergleiche zuerst natürliche Zahlen vor dem Komma.
  0 E = 0 E Beide Zahlen sind gleich groß.
  Vergleiche dann die Zehntel.
  5 z < 2 z 5 ist größer als 2.
  Das Ergebnis steht fest, du musst die Hundertstel nun nicht mehr vergleichen.
  Der Dezimalbruch 0,5 ist größer als 0,23.
  Anmerkung
  Ein anderer Lösungsweg ist das Abschätzen und Vergleichen mit dir bekannten Dezimalbrüchen.Du weißt, dass 0,25 die Hälfte von 0,5 ist. 0,23 ist 2 Hundertstel kleiner als 0,25, also erst recht kleiner als 0,5.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Vergewissere dich, ob die Zahlen vor dem Komma gleich sind (wie 5,3 und 5,23). Danach vergleichst du die Zahlen nach dem Komma (also 5,3 und 5,23).
  Wichtig:
  5,3 hat denselben Wert wie 5,30 (die 3 ist also eine 30 und keine wortwörtliche 3 - nicht 5,03!). Somit ist die erste Zahl größer als die zweite.
3. 2,7 und 2,70
  >
  $<$
  $=$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vergleichen von Dezimalzahlen
  Gliedere Zahl nach Einern (E), Zehnteln (z) und Hundertsteln (h) auf.
  2,7: 2 E 7 z 0 h 2,70: 2 E 7 z 0 h
  Die beiden Zahlen sind gleich groß. Nullen am Ende der Zahl hinter dem Komma ändern deren Wert nicht.
  2,7 = 2,70
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Vergewissere dich, ob die Zahlen vor dem Komma gleich sind (wie 5,3 und 5,23). Danach vergleichst du die Zahlen nach dem Komma (also 5,3 und 5,23).
  Wichtig:
  5,3 hat denselben Wert wie 5,30 (die 3 ist also eine 30 und keine wortwörtliche 3 - nicht 5,03!).
4. 0,08 und 0,1
  $<$
  $>$
  $=$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vergleichen von Dezimalzahlen
  
  Gliedere Zahl nach Einern (E), Zehnteln (z) und Hundertsteln (h) auf.
  0,08: 0 E 0 z 8 h 0,1: 0 E 1z 0 h
  Vergleiche zuerst die natürlichen Zahlen vor dem Komma.
  0 E = 0 E
  Beide Zahlen sind gleich groß.
  Vergleiche dann die Zehntel.
  0 z < 1 z
  0 ist kleiner als 1.
  Somit ist der Dezimalbruch 0,08 kleiner als 0,1. Du musst die Hundertstel nun nicht mehr vergleichen.
  0,08 < 0,1
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Vergewissere dich, ob die Zahlen vor dem Komma gleich sind (wie 5,3 und 5,23). Danach vergleichst du die Zahlen nach dem Komma (also 5,3 und 5,23).
  Wichtig: 5,3 hat denselben Wert wie 5,30 (die 3 ist also eine 30 und keine wortwörtliche 3 - nicht 5,03!).
4
Welche Dezimalzahlen sind durch die Fragezeichen markiert?
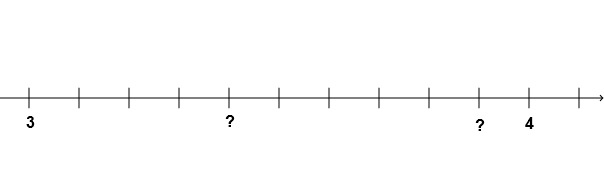
1. Welche Zahl ist größer?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dezimalbrüche
  Am Zahlenstrahl ist der Bereich zwischen der Zahl 3 und der Zahl 4 durch 10 Abschnitte aufgeteilt.
  Berechne den Abstand zwischen 3 und 4.
  $4 - 3 = 1$
  Teile die Zahl 1 in 10 Teile auf.
  $1 : 10 = \frac{1}{10} = 0,1$
  Jeder Abschnitt entspricht also 0,1.
  Erste Zahl
  Zähle ab, hinter welchem Abschnitt sich die linke Dezimalzahl befindet.
  Die linke Zahl befindet sich hinter dem vierten Abschnitt.
  Zähle zur Zahl 3 die 4 Zehntel hinzu.
  $3 + 4 \cdot 0,1 = 3,4$
  Zweite Zahl
  Zähle ab, hinter welchem Abschnitt sich die rechte Dezimalzahl befindet.
  Die rechte Zahl befindet sich hinter dem neunten Abschnitt.
  Zähle zur Zahl 3 die 9 Zehntel hinzu.
  $3 + 9 \cdot 0,1 = 3,9$
  Größenvergleich
  Man sieht am Zahlenstrahl bzw. durch den Vergleich der Dezimalbrüche, dass die zweite Zahl größer als die erste Zahl ist.Also gilt $3,4 < 3,9$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Welche Zahl ist größer?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dezimalbrüche
  Am Zahlenstrahl ist der Bereich zwischen der Zahl $0,1$ und der Zahl $0,2$ durch $10$ Abschnitte aufgeteilt.
  Berechne den Abstand zwischen $0,1$ und $0,2$ (wie bei Teilaufgabe a)).
  $0,2 - 0,1 = 0,1$
  Teile die Zahl 1 in 10 Teile auf.
  $0,1 : 10 = \frac{1}{100} = 0,01$
  Ein Abschnitt entspricht also $0,01$ .
  Erste Zahl:
  Zähle ab, bei hinter welchem Abschnitt sich die linke Dezimalzahl befindet.
  Die linke Zahl befindet sich hinter dem zweiten Abschnitt.
  $0,1 + 2 \cdot 0,01 = 0,12$
  Zähle zu der Zahl $0,1$ noch $2$ Hundertstel hinzu.
  Zweite Zahl:
  Zähle ab, bei welchem Strich sich die rechte Dezimalzahl befindet.
  Die rechte Zahl befindet sich hinter dem siebten Abschnitt.
  $0,1 + 7 \cdot 0,01 = 0,17$
  Zähle zur Zahl $0,1$ die $7$ Hundertstel hinzu.
  Man sieht am Zahlenstrahl bzw. durch den Vergleich der Dezimalbrüche, dass die zweite Zahl größer als die erste Zahl ist. Also gilt $0,12 < 0,17$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

T	H	Z	E	,	z	h	t
0	0	0	2	,	7	0	0

T	H	Z	E	,	z	h	t
0	0	0	2	,	0	8	0

T	H	Z	E	,	z	h	t
			0	,	7	5

T	H	Z	E	,	z	h	t
		1	2	,	5	9	8

T	H	Z	E	,	z	h	t
			0	,	0	0	5

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zum Ordnen von Dezimalbrüchen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

﻿

Hast du eine Frage oder Feedback?

Anmerkung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

﻿

Hast du eine Frage oder Feedback?

Erste Zahl

Zweite Zahl

Größenvergleich

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?