Das Multiplizieren mit v′(x) heißt auch Nachdifferenzieren.
Um die Ableitung der Verkettung von u und v zu berechnen, setzt man also v(x) in die Ableitung u′ ein und differenziert nach.
Einfach gesagt: "Äußere Ableitung mal innere Ableitung":
Zerlegung der Funktion in innere und äußere Funktionen
Betrachten wir als Beispiel die verkettete Funktion f mit f(x)=(x+1)2. Wir möchten sie mit der Kettenregel ableiten. Dazu muss f zunächst in die beiden Teilfunktionen u und v zerlegt werden.
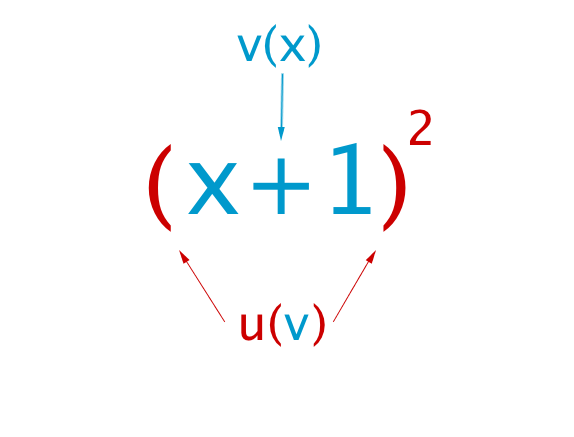
Diese Zerlegung veranschaulichen wir, indem wir u als "a¨ußere Funktion" und v als "innere Funktion" betrachten. Im Beispiel ist die innere Funktion v(x)=x+1. Die äußere Funktion ist die Quadratfunktion, also u(v)=v2.
Setzen wir den inneren Funktionsterm von v(x) in den äußeren Funktionsterm von u ein, erhalten wir die Verkettung der beiden Funktionen: f(x)=u(v(x)),
Das führt wie gewünscht zur Ausgangsfunktion f(x)=(x+1)2.
Die umgekehrte Reihenfolge bei der Verkettung führt in der Regel zu einer völlig anderen Funktion.
v(u(x))=u(v(x))
Beispiel:
u(x)=x2 und v(x)=x+1
u(v(x))=(x+1)2
v(u(x))=x2+1
Mit der nachfolgenden Animation kannst du dir die (punktweise) Entstehung des Schaubildes einer verketteten Funktion aus den Schaubildern der inneren und äußeren Funktionen mit verschiedenen Beispielen veranschaulichen.
Video zur Kettenregel
Beispiele zur Kettenregel
Funktion f(x)=u(v(x))
äußere Funktion u(x)
innere Funktion v(x)
f(x)=(2x−1)3
u(x)=x3
v(x)=2x−1
f(x)=sin(x+2π)
u(x)=sin(x)
v(x)=x+2π
f(x)=ex2+1
u(x)=ex
v(x)=x2+1
Anwendung der Kettenregel am Beispiel
Berechne die Ableitung der Funktion f(x)=sin(x4+2x2).
Zunächst zerlegt man f in u und v mit f(x)=u(v(x)).
Dann berechnet man die Ableitungen von u und v …
… und setzt v(x) in u′ ein.
Zuletzt muss man noch nachdifferenzieren und erhält insgesamt die Ableitung von f.
