Die Grenzwertbetrachtung dient dazu, das Verhalten einer Funktion und ihres Graphen entweder im Unendlichen oder an einer bestimmten Stelle (meist einer Definitionslücke) zu ermitteln.
Das funktioniert, indem man x immer näher an die gewünschten Werte annähert und dabei überprüft, wie sich die zugehörigen y-Werte der Funktion verhalten.

Verhalten im Unendlichen
prüft das Verhalten einer Funktion (des y-Wertes), wenn sich x an und annähert.
Diese Darstellung beinhaltet folglich zwei Untersuchungen, die getrennt voneinander durchgeführt werden.
Bestimmung der Grenzwerte durch Ausprobieren
Man ersetzt x durch einen sehr hohen positiven und einen sehr hohen negativen Wert und betrachte, wie sich der y-Wert der Funktion dabei verhält.
Beispiel:
Gesucht ist der Grenzwert mit .
Setze große Zahlen für ein und stelle eine Vermutung über den Grenzwert auf.
Vermutung:
Berechnung des Grenzwerts
Um den Grenzwert sicher korrekt zu erhalten, ist es jedoch erforderlich, den Funktionsterm mit entsprechenden, von der Art des betreffenden Terms abhängigen Methoden genauer zu untersuchen, und den Grenzwert durch Berechnen zu bestimmen.
Durch die Berechnung des Grenzwerts im Unendlichen erhält man den Wert der waagerechten Asymptote, falls vorhanden.
Verhalten an der Definitionslücke
prüft das Verhalten einer Funktion (des y-Wertes), wenn sich der Definitionslücke annähert.
Linksseitiger und rechtsseitiger Grenzwert
Man kann allerdings nicht automatisch davon ausgehen, dass sich der Funktionsgraph von links und von rechts betrachtet gleich verhält.
beinhaltet also zwei Untersuchungen, die getrennt voneinander durchgeführt werden.
Das Verhalten der Funktion an der Definitionslücke muss von beiden Seiten betrachtet werden.
Ist zum Beispiel , betrachtet man das Verhalten der Funktion bei 1,9999… und bei 2,000…1, da man sich einmal von links und einmal von rechts an den Punkt 2 annähert.
Beispiel
Verhalten an der Definitionslücke der Funktion :
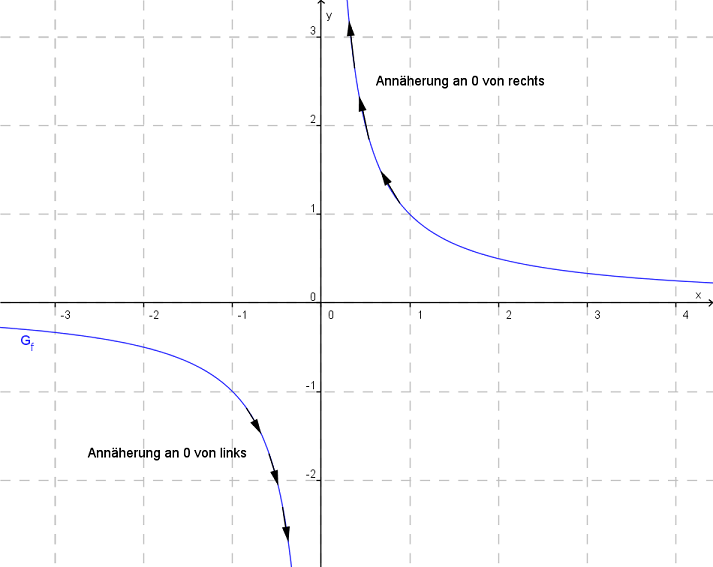
Das berechnet man so:
Rechtsseitiger Grenzwert:
da man hier von einem Wert knapp über null ausgeht.
Linksseitiger Grenzwert:
da man hier von einem Wert knapp unter null ausgeht.
Durch diese Berechnung erhält man entweder den Wert:
oder einer senkrechte Asymptote durch eine Polstelle
oder bei einer Funktion mit Sprung die Werte an der Unstetigkeitsstelle.
In diesem Beispiel verläuft durch die Polstelle eine senkrechte Asymptote.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
