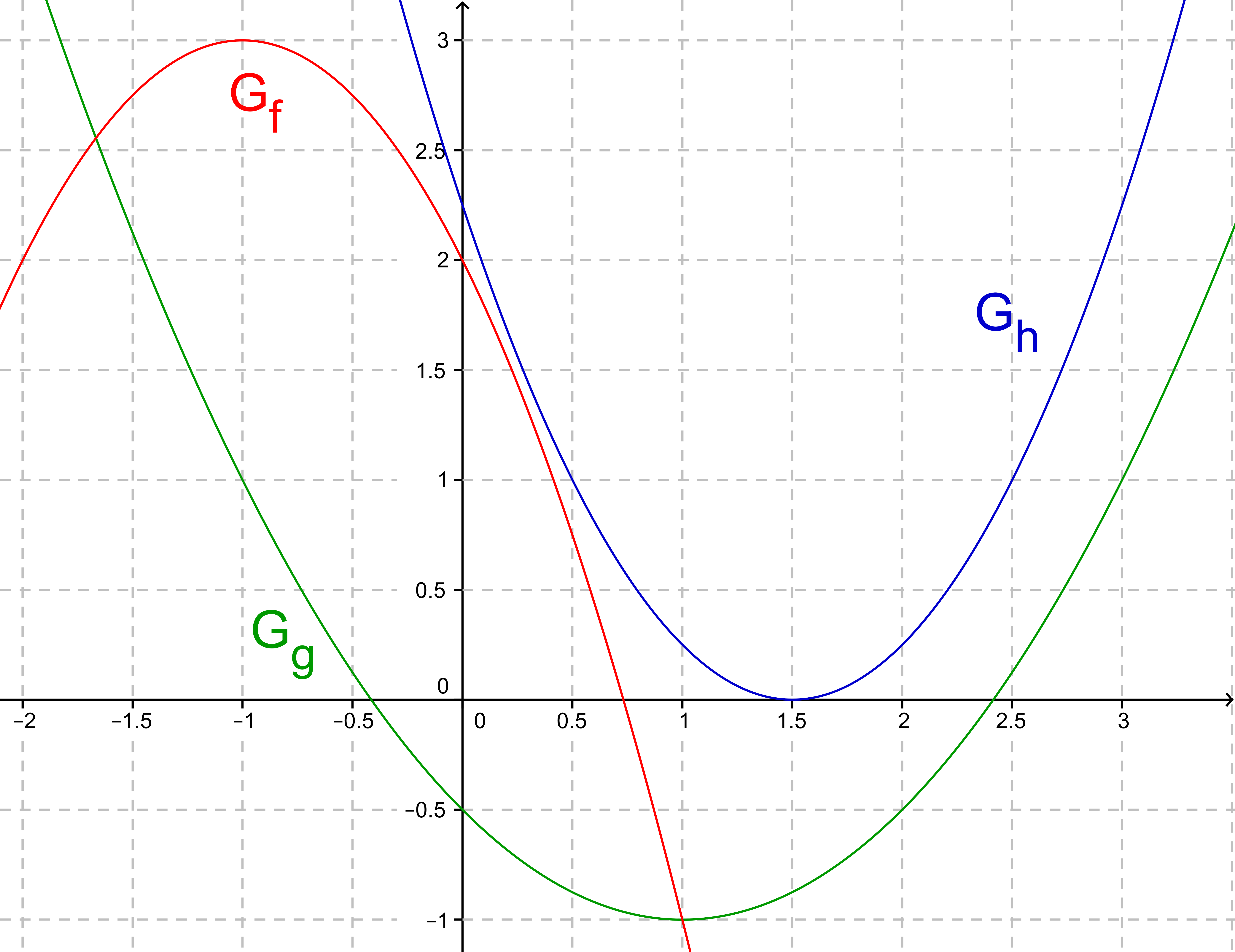
Lies aus nachstehender Abbildung mögliche Funktionsterme der Funktionen , und ab.
Bestimme die Lösungsmenge der Gleichung .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Lies aus nachstehender Abbildung mögliche Funktionsterme der Funktionen , und ab.
Bestimme die Lösungsmenge der Gleichung .
