Determinanten berechnen

Je nach Größe der Matrix entscheidet man sich für den Laplace'schen Entwicklungssatz oder die Regel von Sarrus zur Berechnung der Determinante dieser Matrix.

Berechnung der Determinante

Nach Formel

$2x2$ Matrix: $\det\begin{pmatrix}a&b\\c&d\end{pmatrix}=\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad-bc$

Regel von Sarrus oder Laplace'sche Entwicklungssatz

$3x3$ Matrix: $\det\begin{pmatrix}a&b&c\\d&e&f\\g&h&i\end{pmatrix}=\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}\\=aei+cdh+bfg-afh-bdi-ceg$

Matrix größer als $3x3$ :

Nur noch Laplace'scher Entwicklungssatz möglich

Eigenschaften

$\det(A)=0$ , wenn…

…eine Zeile/Spalte aus Nullen besteht

…zwei Zeilen/Spalten gleich sind

…eine Zeile das Vielfache einer anderen Zeile ist

Regel von Sarrus (3x3 Matrizen)

Diese Regel gilt nur für $A\in{\mathrm{Mat}}_{3\times3}$ , also darf sie nur bei 3x3-Matrizen angewendet werden!

\displaystyle \det A=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}

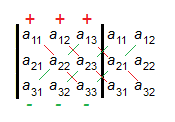
Man schreibt die erste und die zweite Spalte nochmal hinter die Matrix und bildet die Diagonalen:

Die Diagonalen von links nach rechts (im Bild rot) werden multipliziert und dann summiert.

Im Gegensatz dazu werden die Diagonalen von rechts nach links (hier grün) multipliziert und dann subtrahiert.

\displaystyle \det A=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}

Laplace'scher Entwicklungssatz (für alle nxn Matrizen)

Das Prinzip des Entwicklungssatzes ist es, die Determinante einer großen Matrix aus den Determinanten von mehreren kleineren Matrizen zu berechnen. Das bezeichnet man auch als entwickeln.

Hier kann man entscheiden, ob man eine Determinante nach den Spalten oder den Zeilen entwickelt.

$\det A=\sum_{i=1}^n(-1)^{i+j}a_{ij}\cdot\det A_{ij}$ Entwicklung nach der j-ten Spalte

$\det A=\sum_{j=1}^n(-1)^{i+j}a_{ij}\cdot\det A_{ij}$ Entwicklung nach der i-ten Zeile

Allgemein bedeutet dies nichts anderes als, dass man sich eine Spalte oder eine Zeile heraussucht, über die man die neuen Determinanten entwickelt:

Zeile

$\begin{vmatrix}\mathrm a&\mathrm b&\mathrm c\\\mathrm d&\mathrm e&\mathrm f\\\mathrm g&\mathrm h&\mathrm i\end{vmatrix}$

Man sucht sich zunächst eine Zeile aus der Matrix aus. Hier zum Beispiel die erste Zeile.

Dann wendet man die Formel für die Entwicklung nach Zeilen an:

$\det A=(-1)^{1+1}a\begin{vmatrix}e&f\\h&i\end{vmatrix}+(-1)^{1+2}b\begin{vmatrix}d&f\\g&i\end{vmatrix}+(-1)^{1+3}c\begin{vmatrix}d&e\\g&h\end{vmatrix}$

Analog funktioniert dies auch bei den Spalten. Es ist egal, welche Spalte oder Zeile man sich aussucht.

Arbeitet man sehr oft damit, stellt man fest, dass sich dies leichter vorstellen lässt:

$\def\arraystretch{1.25} \left|\begin{array}{cccc}+&-&+&\cdots\\-&+&-&\cdots\\+&-&+&\cdots\\\vdots&\vdots&\vdots&\ddots\end{array}\right.$

Egal wie groß die quadratische Matrix ist, die Vorzeichen lassen sich immer wie in der Abbildung weiter führen.

Man nimmt sich nun also eine Spalte oder eine Zeile. Nimmt den ersten Wert der Spalte / Zeile, wählt nach der Abbildung das Vorzeichen aus und multipliziert diesen Wert dann mit der Matrix, die dabei herauskommt, wenn man die Spalte und Zeile ausstreicht, auf der sich der Wert befindet. Dies macht man mit allen Teilstücken der Zeile/Spalte und ist dann fertig.

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?