Gemischte Aufgaben
Hier findest du gemischte Aufgaben zu verschiedenen Rechenmethoden in der Vektorrechnung. Lerne, Längen, Flächeninhalte und weitere Größen zu bestimmen!
- 1
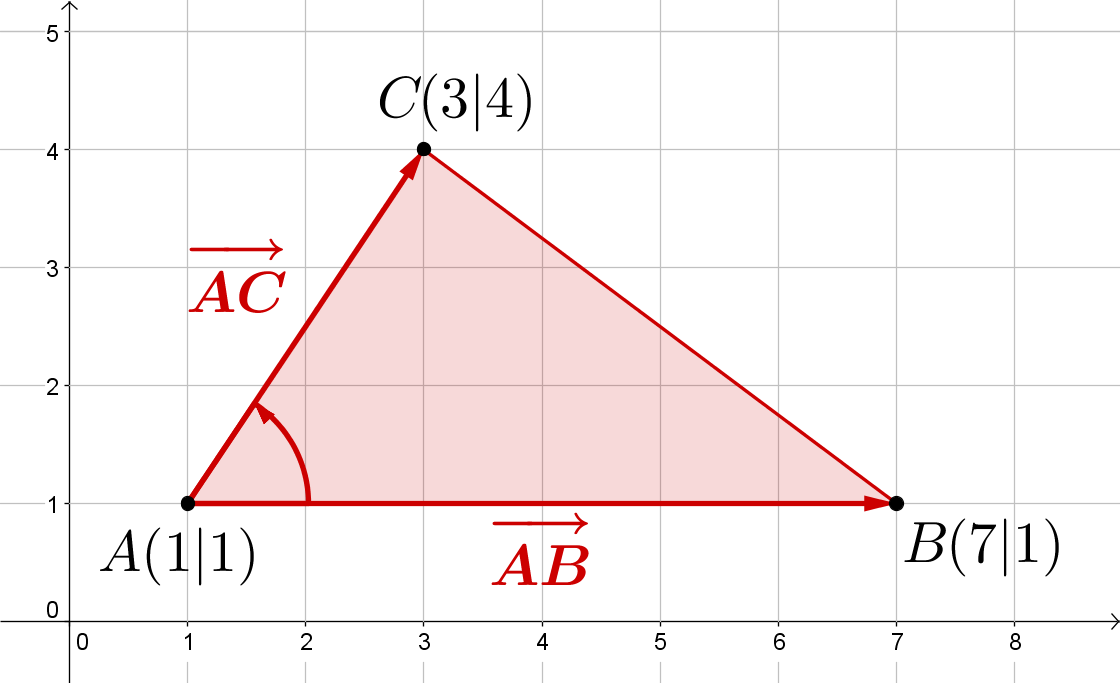
Gegeben sind die Punkte , und sowie die Vektoren und .
Berechne jeweils die Länge der Vektoren und !
Berechne das Skalarprodukt der Vektoren und sowie das Maß des (spitzen) Winkels , den sie einschließen!
Zeichne das Dreieck und berechne seinen Flächeninhalt mithilfe der Determinante!
- 2
Gegeben sind die Punkte , , .
Berechne alle Seitenlängen des Dreiecks
Prüfe, ob das Dreieck rechtwinklig ist.
Berechne alle Winkel des Dreiecks .
- 3
Ordne richtig zu!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?