Der Flächeninhalt eines Dreiecks berechnet sich üblich über die Formel
wobei die Grundlinie und die Höhe des Dreiecks ist.
Auf folgende andere Arten lässt sich der Flächeninhalt auch berechnen:
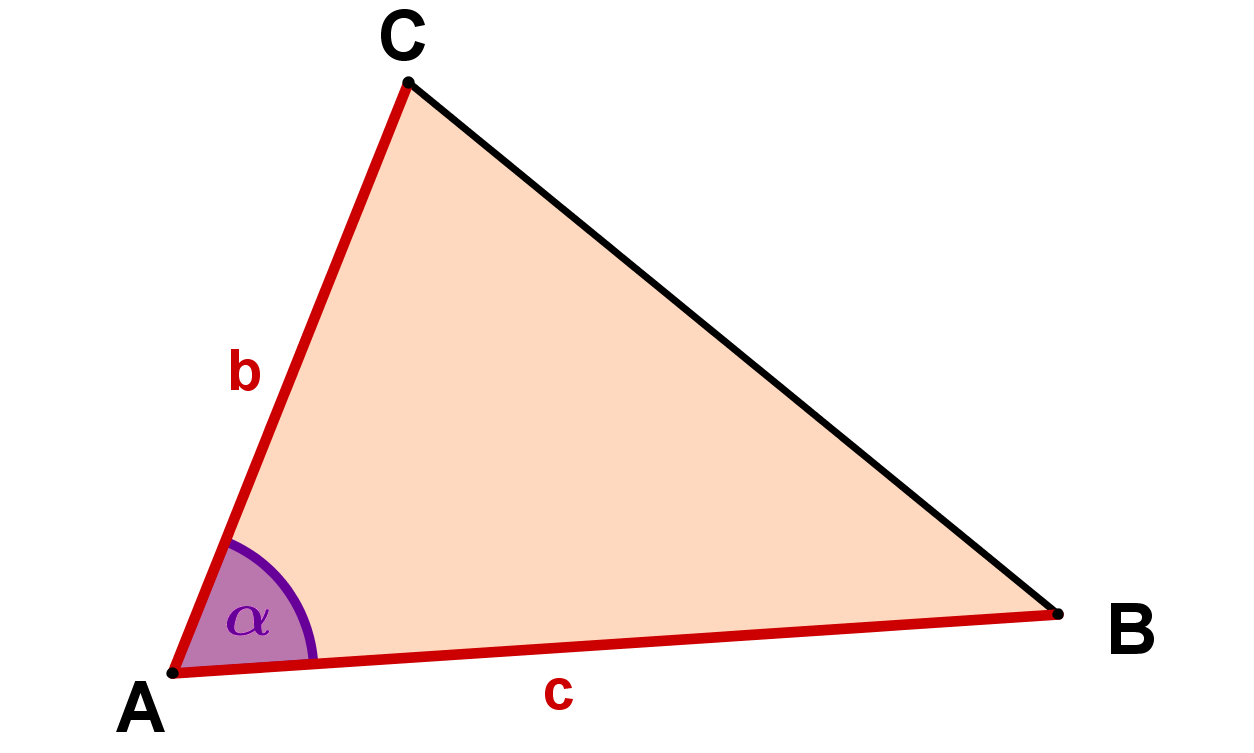
1. Berechnung mit zwei Seiten des Dreiecks (z.B. und ) und dem Sinus des Winkels dazwischen (hier ):

2. Berechnung mit dem Kreuzprodukt oder einer Determinante (nur im Koordinatensystem möglich)

Diese insgesamt 3 verschiedenen Berechnungsarten werden nun genauer erklärt.
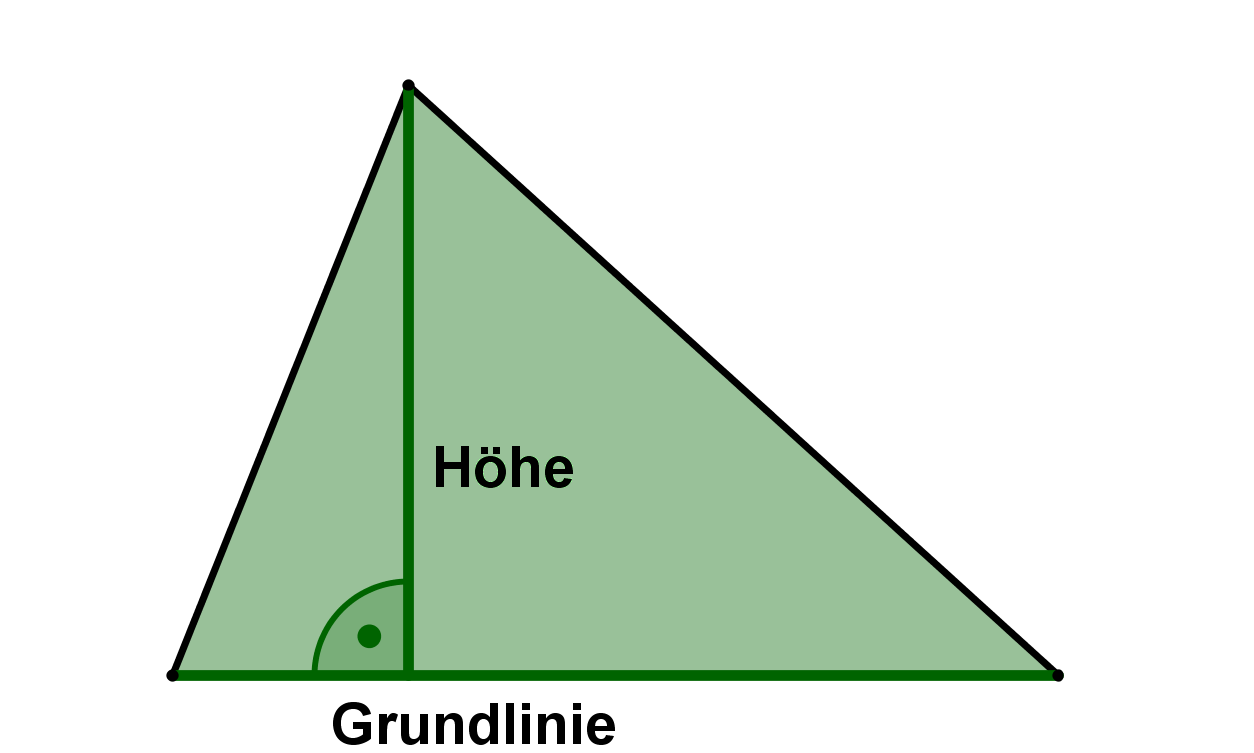
Dreiecksfläche mit Grundlinie und Höhe berechnen
Dies ist die häufigst verwendete Methode. Man braucht dabei zur Berechnung der Dreiecksfläche
die Grundlinie und
die Höhe des Dreiecks.

Die Formel lautet:
Verschiedene Versionen der Formel
Grundlinie kann jede beliebige Seite des Dreiecks sein; muss aber die jeweils zugehörige Höhe sein. Damit kann die Formel in drei verschiedenen Formen erscheinen:
Grundlinie | Höhe | Formel | Darstellung |
|---|---|---|---|
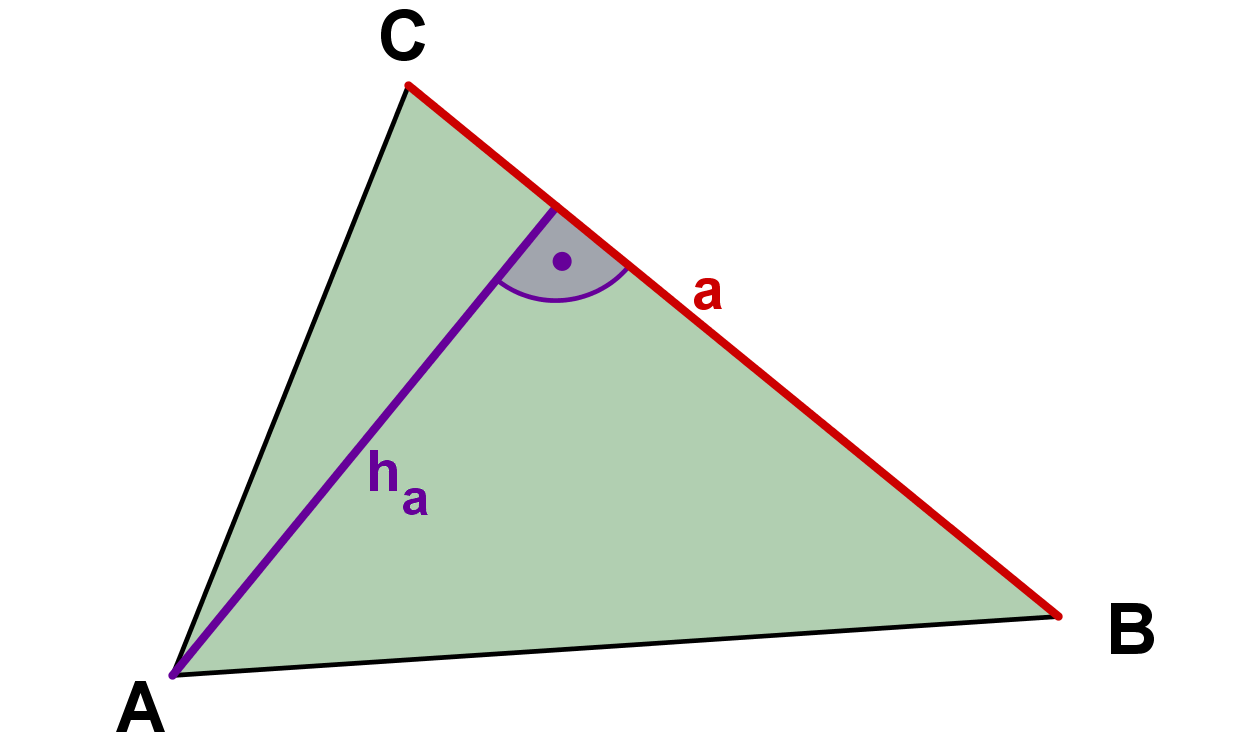 | |||
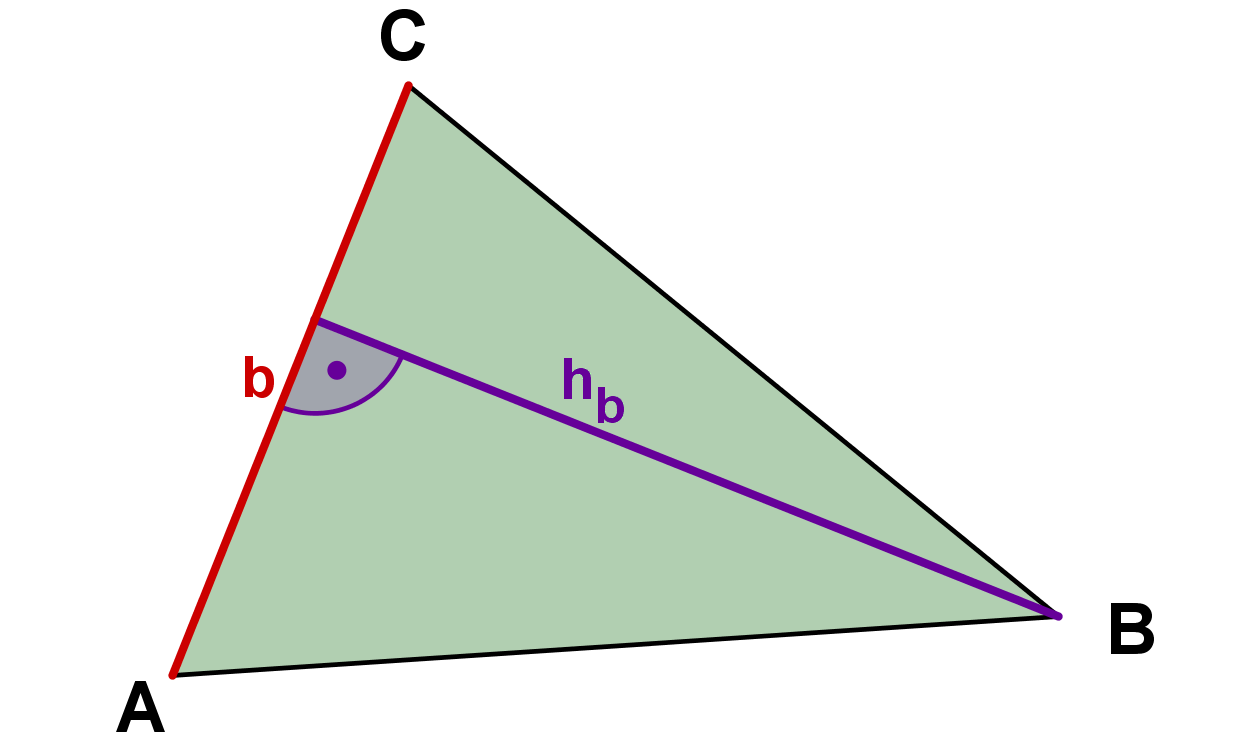 | |||
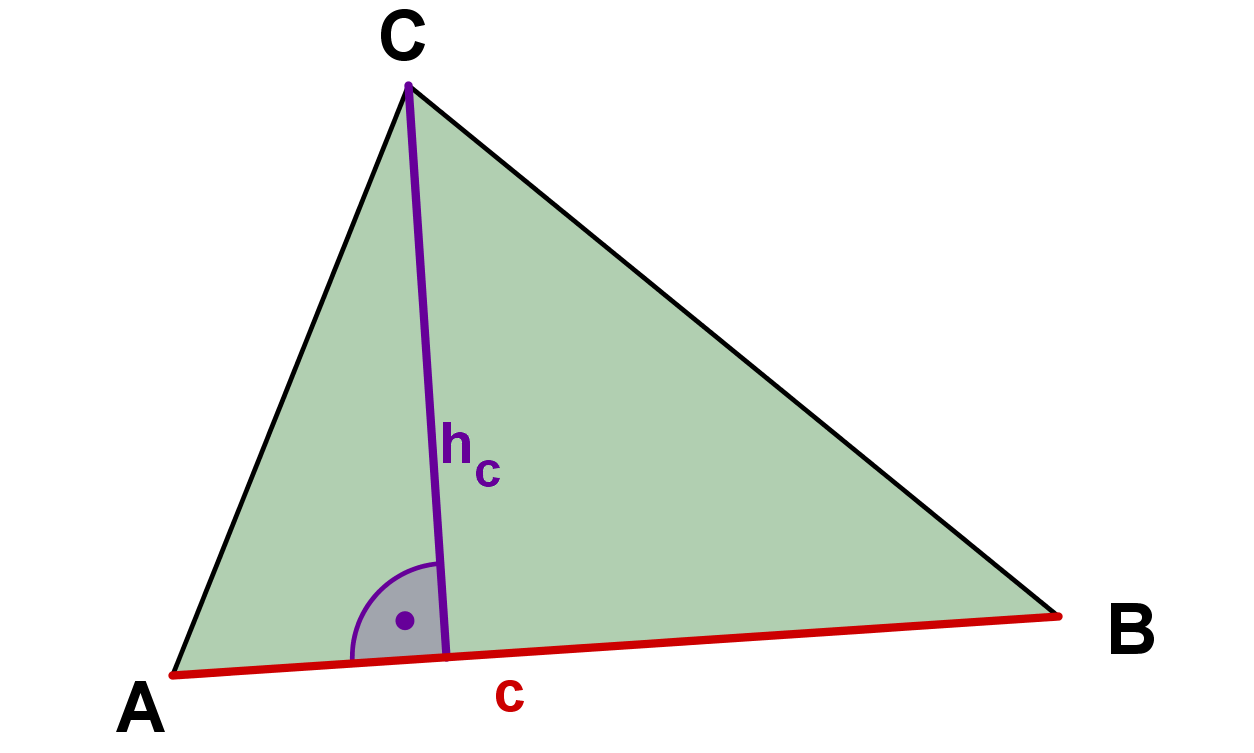 |
Über alle drei Formeln ergibt sich der gleiche Flächeninhalt! Wähle in einer Aufgabe eine der drei Formeln so, dass sie am leichtesten zu berechnen ist.
Sonderfall: rechtwinkliges Dreieck
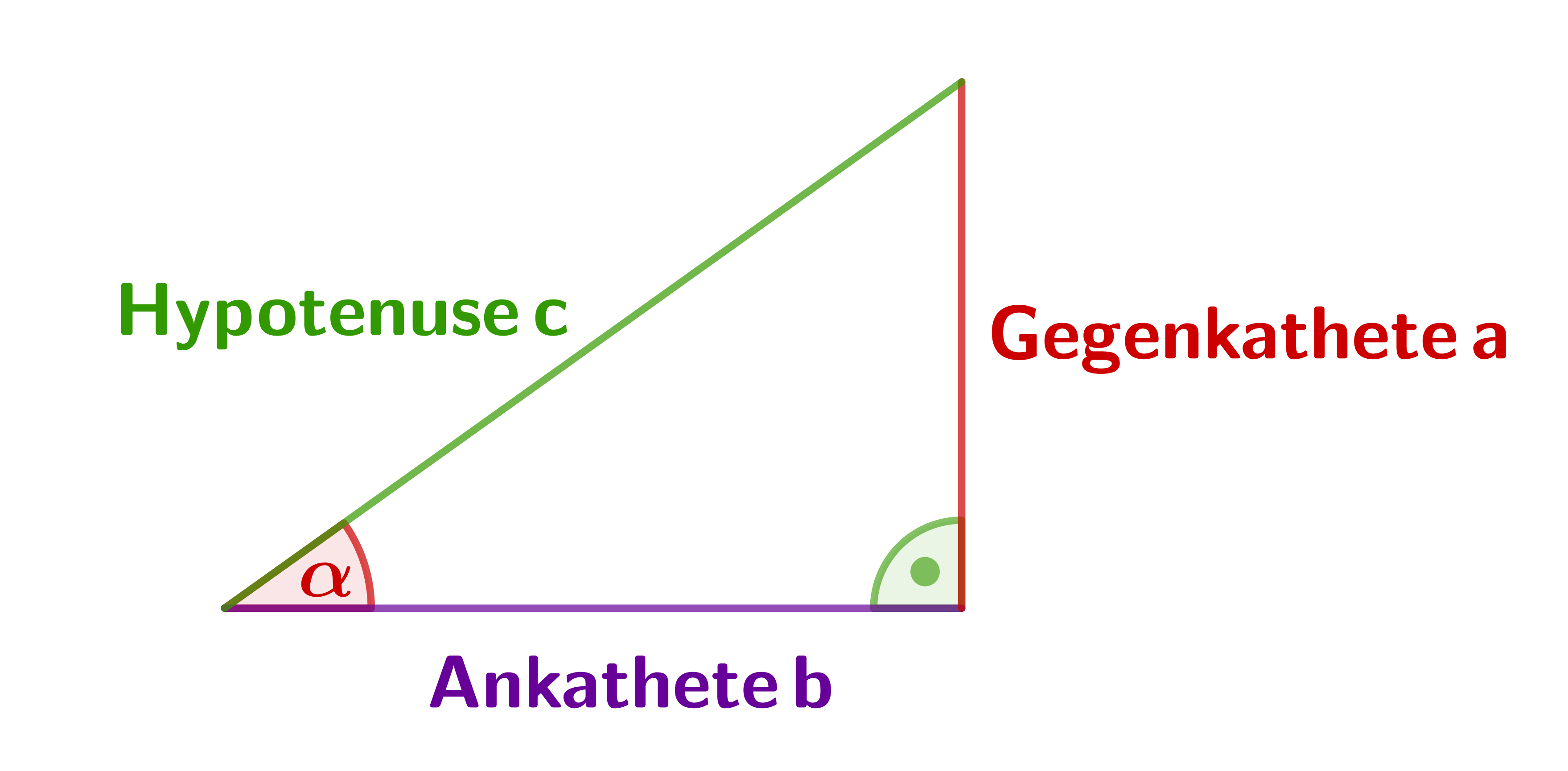
In einem rechtwinkligen Dreieck mit den Katheten und gilt:
(Die Formel gilt natürlich immer noch.)
Sonderfall: gleichseitiges Dreieck
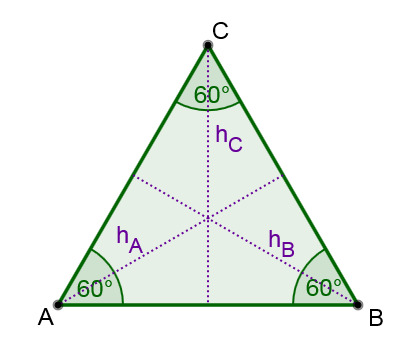
In einem gleichseitigen Dreieck mit Seitenlänge gilt:
Dreiecksfläche mit dem Sinus berechnen
Wenn man bereits den Sinus kennt, kann man die Fläche eines Dreiecks auch mit folgenden Angaben berechnen:
zwei Seitenlängen und
dem Sinus des dazwischenliegenden Winkels
Also z.B.:
ODER
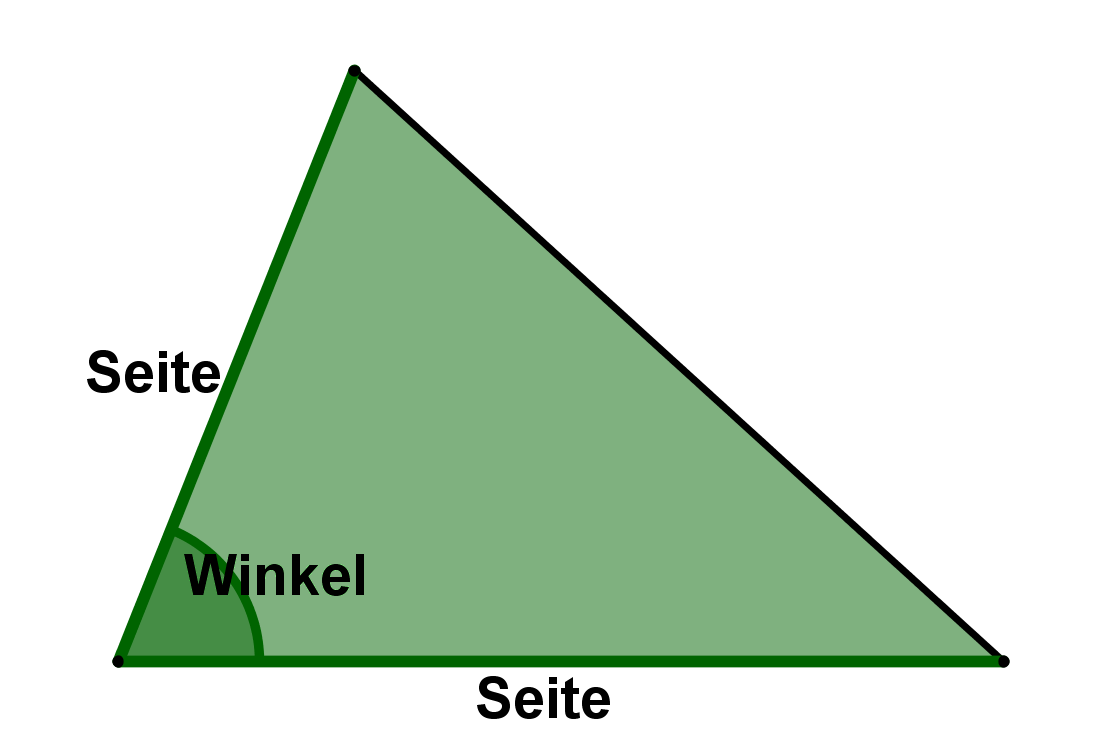
Statt kann natürlich auch jeder andere Winkel des Dreiecks betrachtet werden, und daher kann die Formel auch wieder in drei verschiedenen Formen auftreten:
Winkel | Formel | Darstellung |
|---|---|---|
 | ||
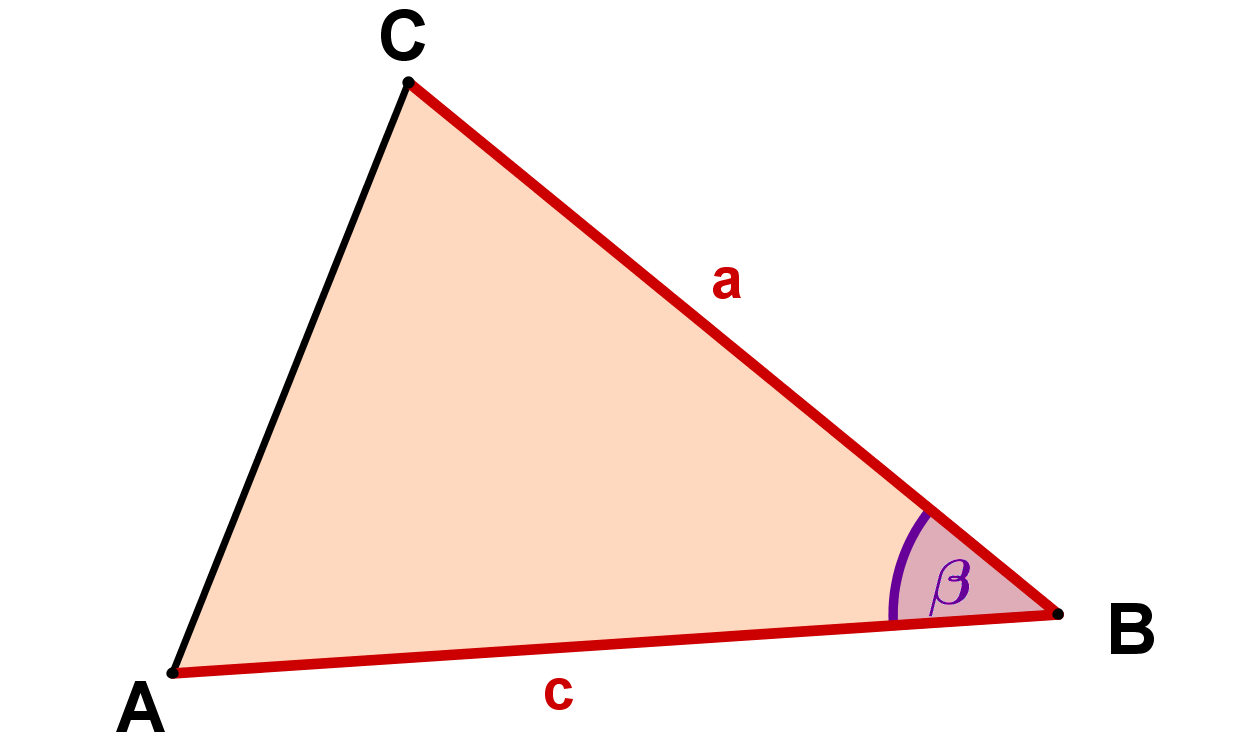 | ||
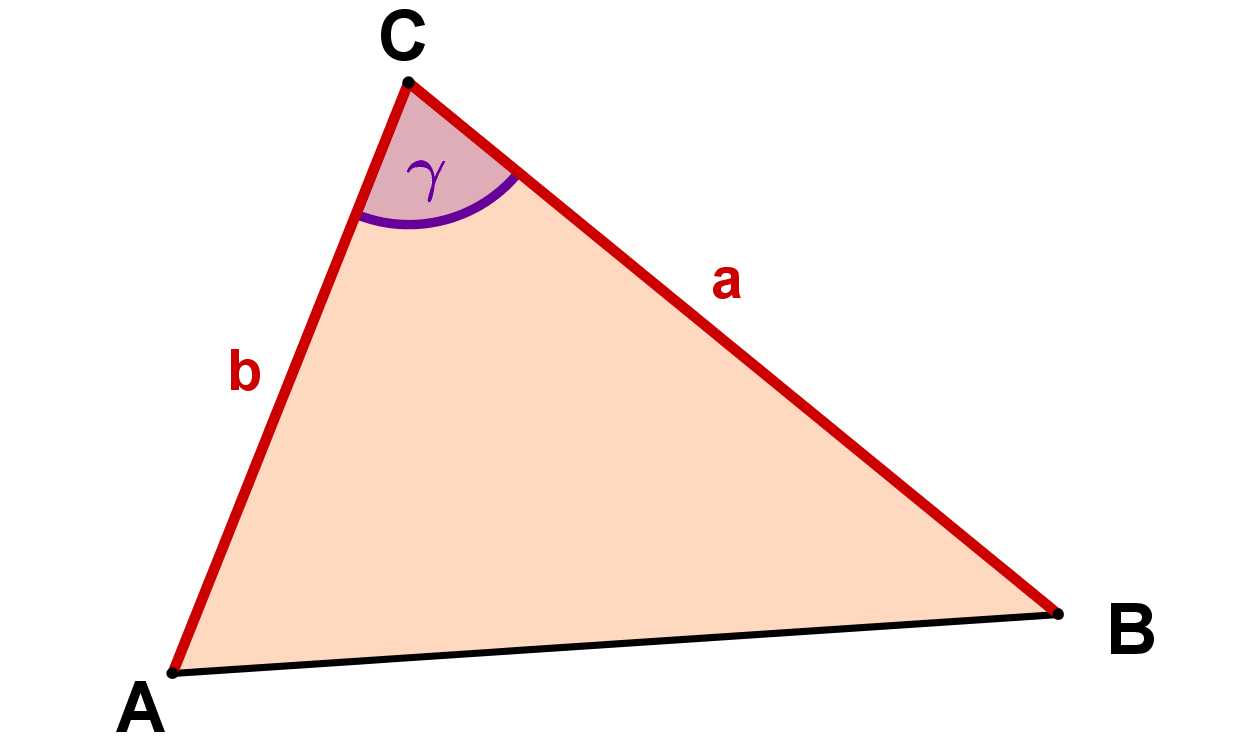 |
Dreiecksfläche mit dem Kreuzprodukt oder der Determinante berechnen
Diese Methode funktioniert nur, wenn das Dreieck in einem Koordinatensystem gegeben ist.
Die Formel lautet:
Du bestimmst also die Verbindungsvektoren und .
Dann berechnest du deren Kreuzprodukt und ...
bestimmst die Länge (also den Betrag) des berechneten Vektors.
Durch Halbieren dieses Werts erhältst du den Flächeninhalt des Dreiecks.

Mehr zum Thema findest du im Artikel Flächeninhalt eines Dreiecks im Koordinatensystem
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
