Der Satz des Thales beschreibt folgenden Zusammenhang:
Zeichne einen Halbkreis und markiere einen Punkt auf dem Kreisbogen. Wenn du diesen Punkt mit den Eckpunkten des Durchmessers verbindest, entsteht ein rechtwinkliges Dreieck. Der rechte Winkel befindet sich gegenüber des Durchmessers des Kreises.
Zudem ist auch die Umkehrung des Satzes richtig.
Vorgehen
Man beginnt mit einer beliebigen Strecke (hier: Strecke ).

Nun konstruiert man einen Thaleskreis (hier mit Mittelpunkt ).
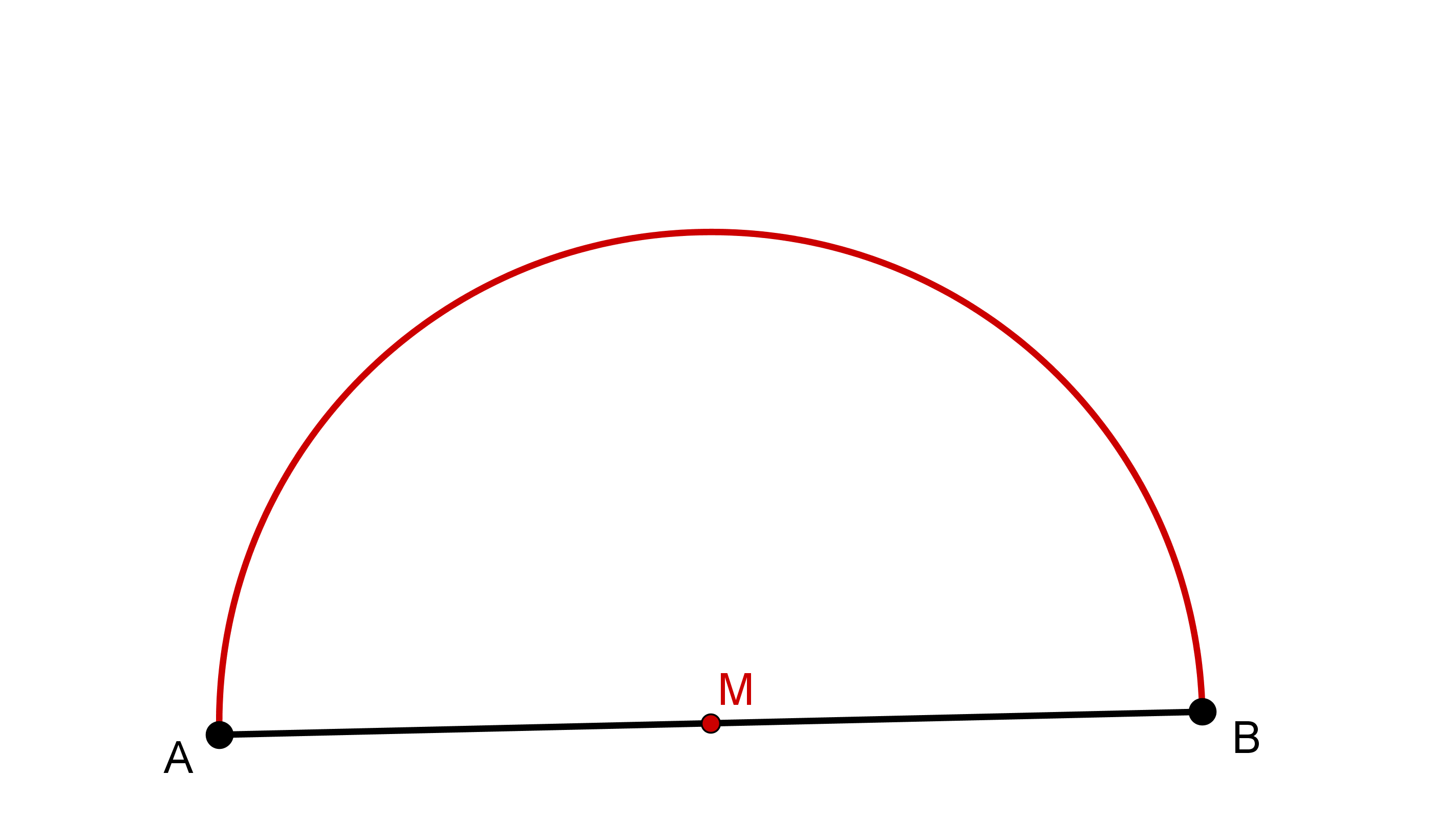
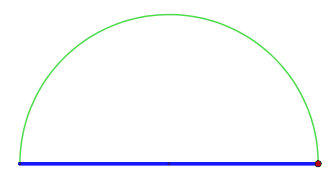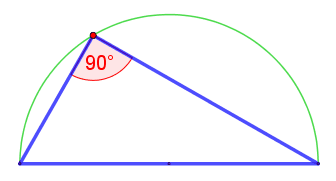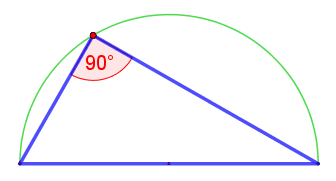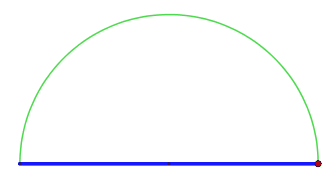
Nun kann man einen beliebigen Punkt auf dem Kreisbogen markieren (hier Punkt ).
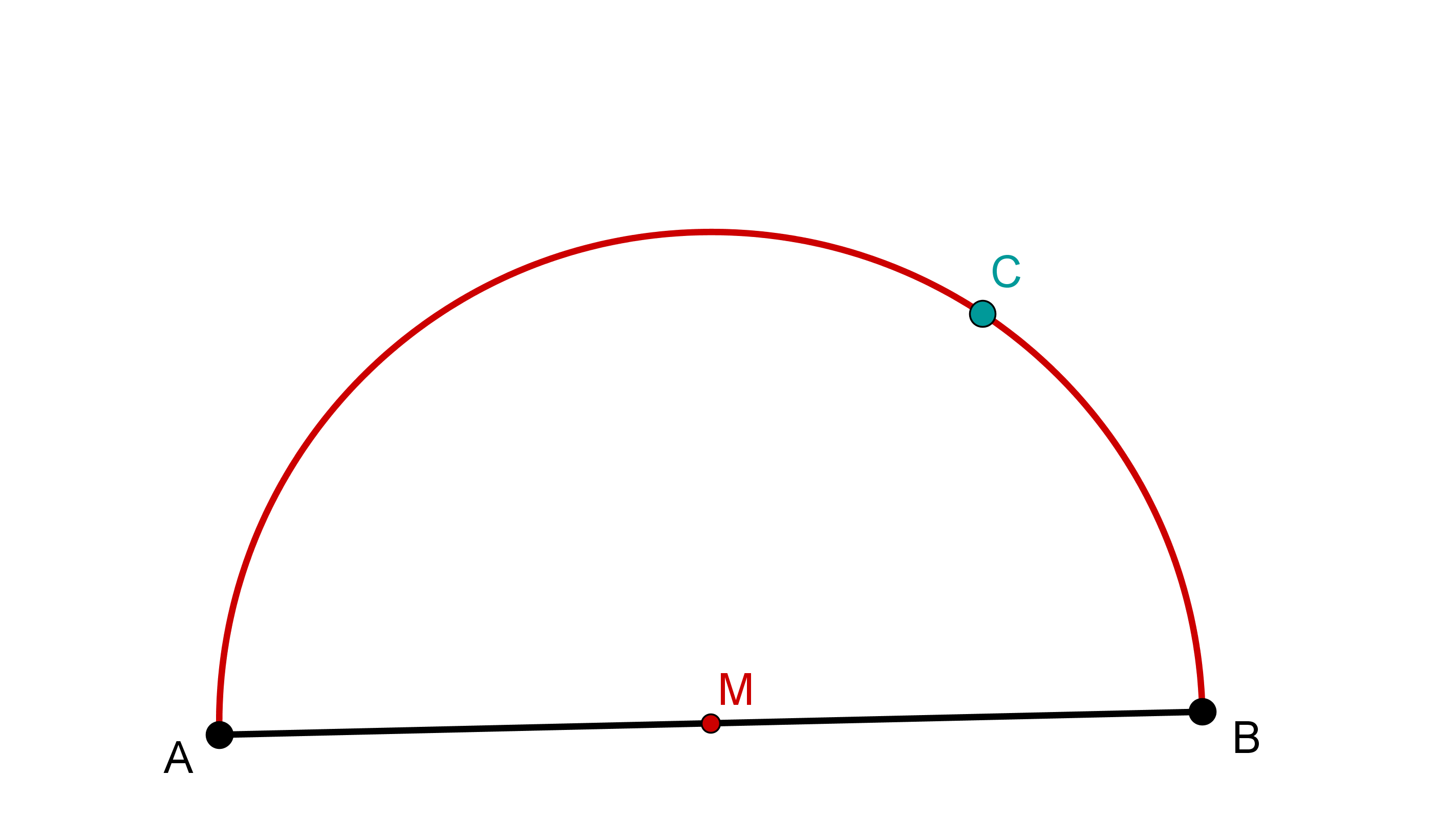
Nun verbindet man die Punkte und zu einem Dreieck.
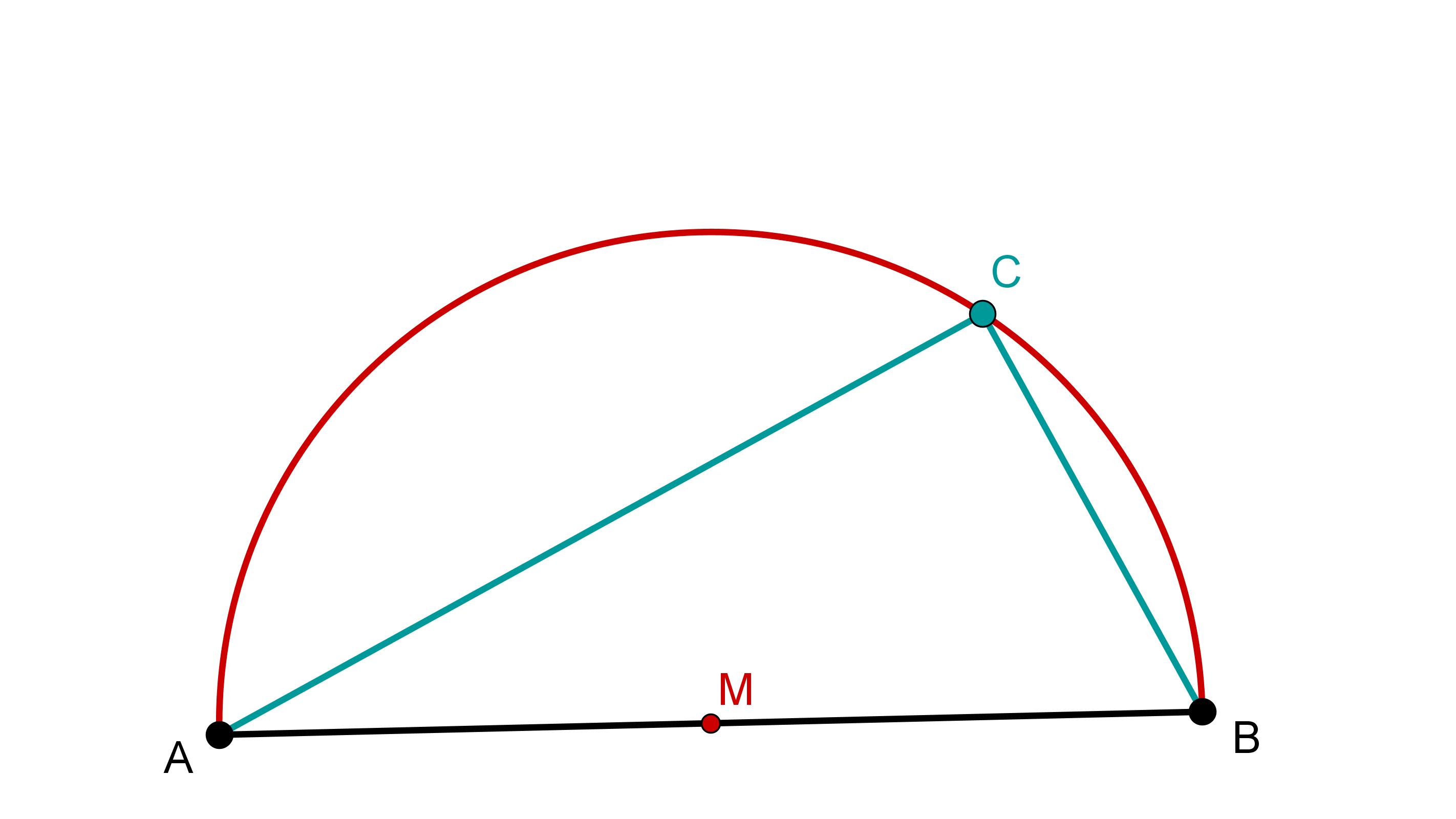
Der Winkel ist ein rechter Winkel.
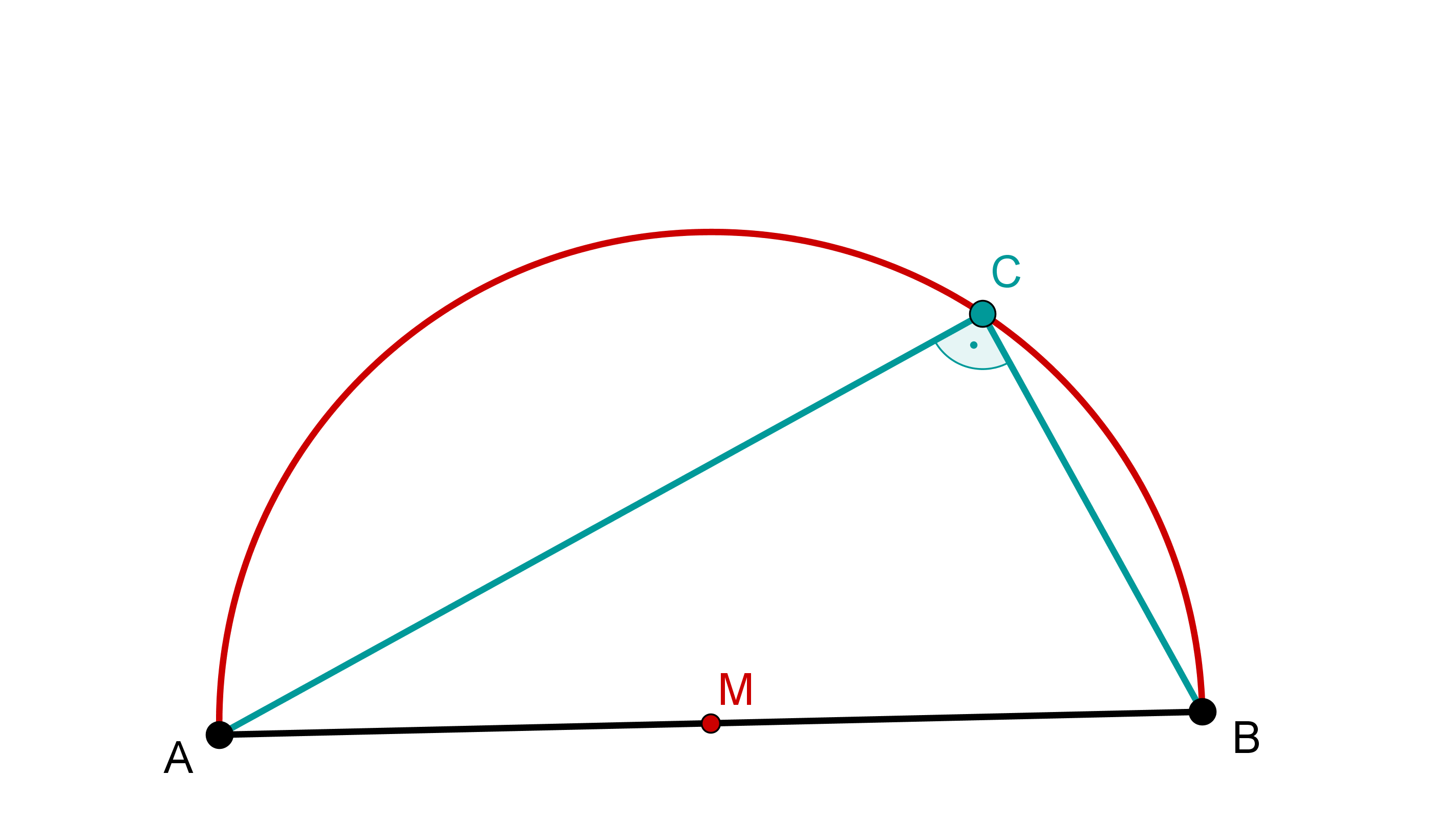
Umkehrung des Satzes des Thales
Es gilt auch die Umkehrung des Satzes:
In einem rechtwinkligen Dreieck ist der Mittelpunkt der Hypotenuse der Mittelpunkt des Umkreises.
Anwendung
Der Thaleskreis ist hilfreich zur Konstruktion rechtwinkliger Dreiecke.
Außerdem kann man mit ihm eine Tangente an einen Kreis konstruieren, die durch einen beliebigen Punkt außerhalb des Kreises verläuft.
Warum gilt der Satz des Thales?
Dass der Satz des Thales immer gilt, zeigt folgender Beweis:
Man zeichnet zuerst ein Dreieck mit Hypotenuse als Durchmesser eines Kreises und den dritten Punkt des Dreiecks auf den Kreisbogen des Kreises (hier: Punkt ).
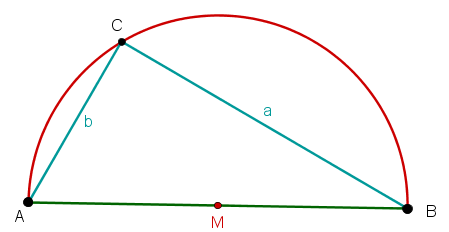
Zusätzlich trägt man die Seitenhalbierende der Hypotenuse ein. Damit entstehen zwei neue Dreiecke:
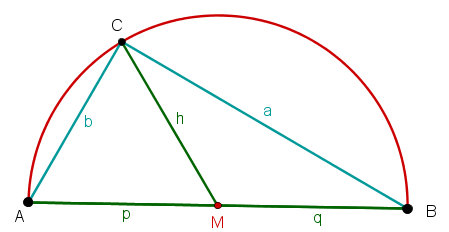
Wenn man die Winkel in den Dreiecken nun noch benennt, erhältst du folgendes Bild:
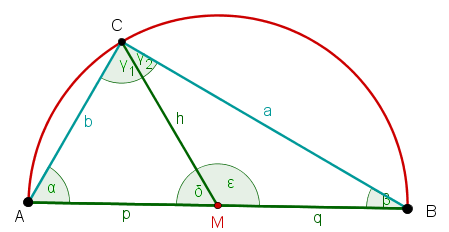
Nun ist bereits bekannt, dass die Innenwinkelsumme eines Dreiecks beträgt.
Also sowohl in dem Dreieck als auch in den Dreiecken und .
Daher folgt:
Außerdem gilt:
Die Dreiecke und sind gleichschenklig, da .
Also:
Damit kommt man auf die Rechnung:
| ↓ | Ersetze und aus der Überlegung von vorhin. | ||
| ↓ | Fasse zusammen. | ||
Damit ist gezeigt, dass der Winkel ein rechter Winkel ist, egal wie man den Punkt auf der Kreisbahn wählt.
Übungsaufgaben
Laden
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Fasskreisbogen und Satz des Thales
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
