Geometrische Graffitis
Zur Verschönerung wird ein Parallelogramm auf drei verschiedene Weisen mit geometrischen Figuren besprüht. (Welches Graffiti würde dir als "Kunstwerk" am besten gefallen?)
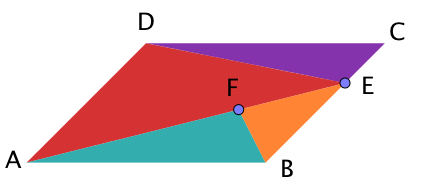
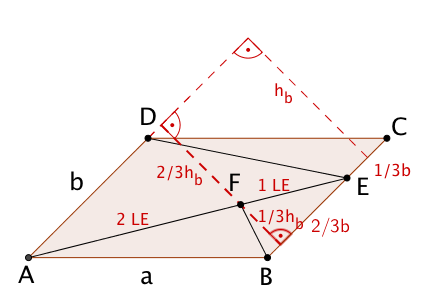
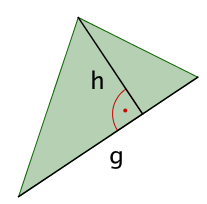
Graffiti 1
Hier gilt:
und
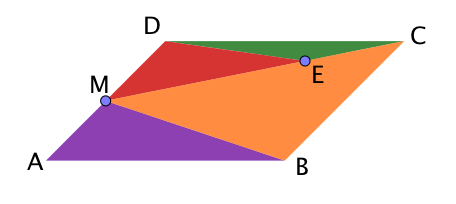
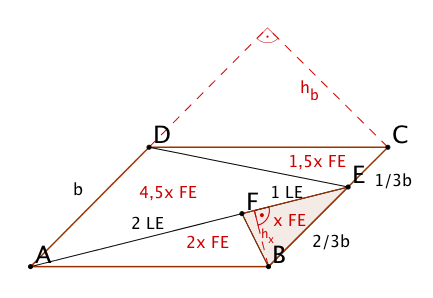
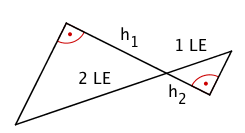
Graffiti 2
Hier gilt:
und
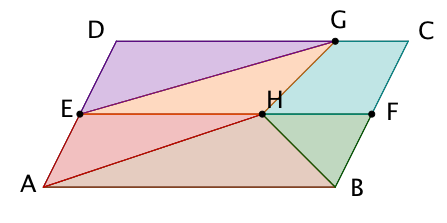
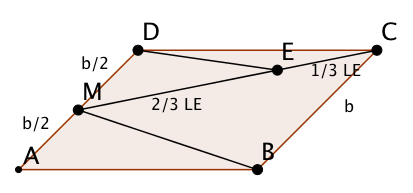
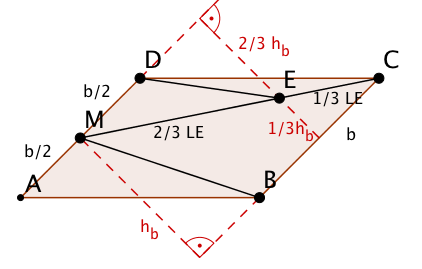
Graffiti 3
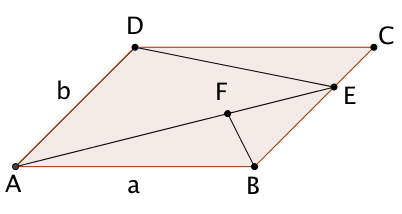
Hier gilt:
ist eine Mittelparallele im Parallelogramm und der Punkt teilt diese im Verhältnis . Der Punkt teilt die Seite im Verhältnis .
Schule dein Empfinden für Flächengrößen und entscheide ohne Rechnung, welche Aussage für das Graffiti 1 zutrifft.
Klicke die deiner Meinung nach zutreffende Aussage an.
Entscheide auch für das Graffiti 2 ohne Rechnung, welche der folgenden Aussagen zutrifft.
Klicke die deiner Meinung nach richtige Aussage an.
Ordne für das Graffiti 1 die Teilflächen der Größe nach und beweise, dass sie im Verhältnis stehen.
Ordne für das Graffiti 2 die Teilflächen der Größe nach und beweise, dass sie im Verhältnis stehen.
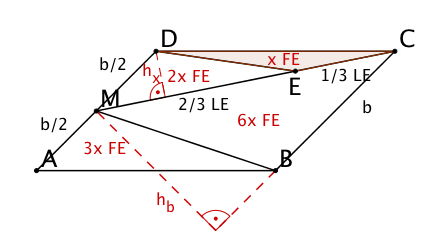
Beweise, dass das Graffiti drei gleich große Teilflächen enthält und die drei anderen im Verhältnis stehen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?