Ein symmetrisches Trapez (manchmal auch "gleichschenkliges Trapez" genannt) ist
ein (besonderes) Viereck, bei dem
(mindestens) zwei gegenüberliegende Seiten parallel sind und
das achsensymmetrisch zur Mittelsenkrechten der beiden parallelen Seiten ist.
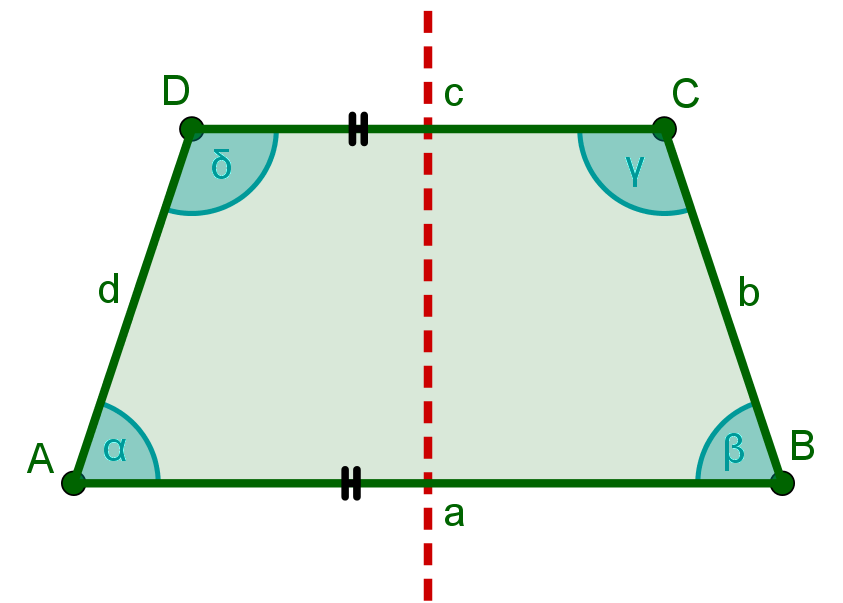
Gleichwertige Definition
Ein symmetrisches Trapez ist ein Trapez, bei dem die beiden Innenwinkel einer der parallelen Seiten gleich groß sind.
Eigenschaften des symmetrischen Trapezes
Besonderheiten bei Seiten, Winkeln und Diagonalen
In einem symmetrischen Trapez
sind die beiden Schenkel gleich lang.
In dem symmetrischen Trapez gilt also:
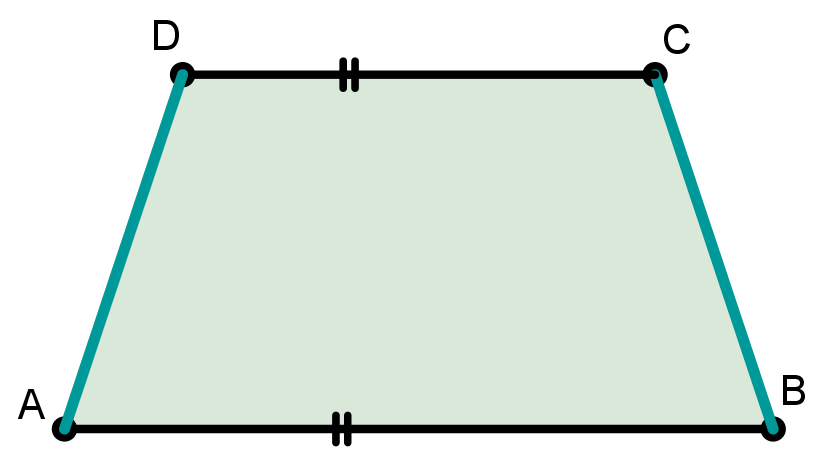
gleich lange Seiten im symmetrischen Trapez
In einem symmetrischen Trapez
gibt es an jeder der parallelen Seiten zwei gleich große Innenwinkel.
In dem symmetrischen Trapez gilt also: ,
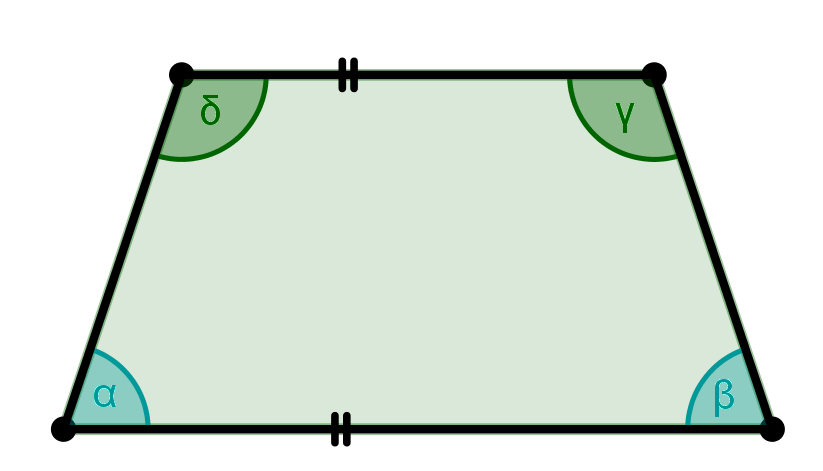
gleich große Winkel im symmetrischen Trapez
Ergänzen sich die Innenwinkel an den beiden Schenkeln zu 180 Grad.
,
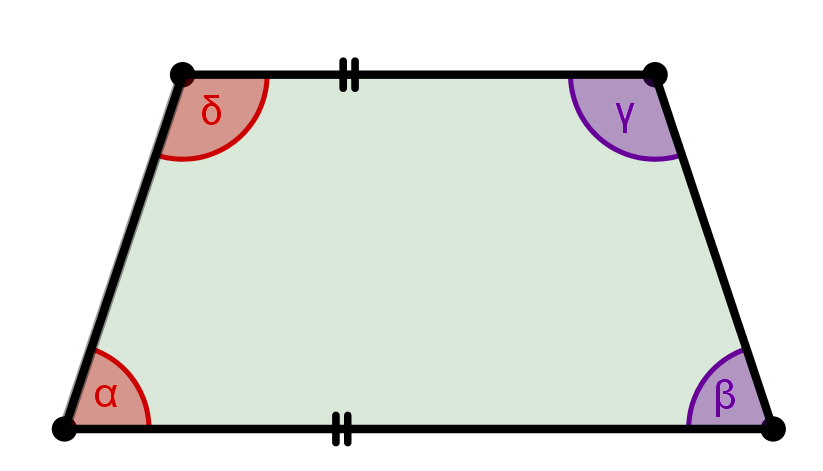
In einem symmetrischen Trapez
sind die Diagonalen gleich lang
In dem symmetrischen Trapez gilt also:
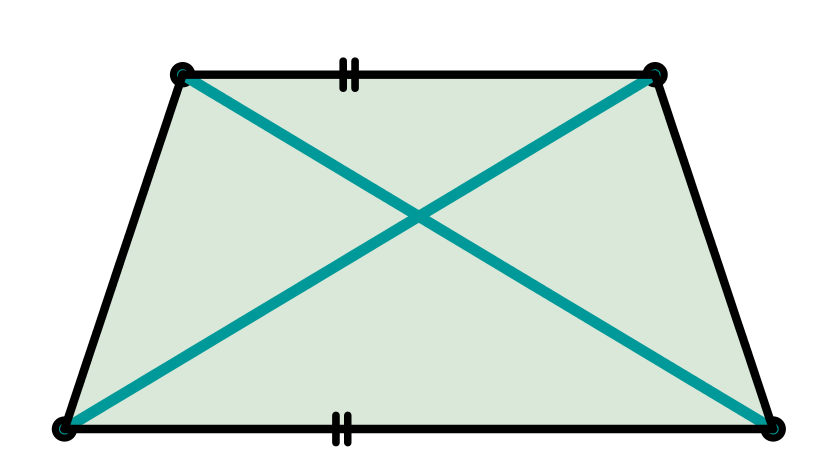
Einordnung als Viereck
Jedes symmetrische Trapez ist immer auch ein Trapez,
und zwar ein (besonderes) Trapez, das achsensymmetrisch ist.
Spezialfälle von symmetrischen Trapezen
Wenn ein symmetrisches Trapez vier rechte Winkel hat, ist es ein Rechteck.
Wenn ein symmetrisches Trapez vier gleich langen Seiten hat, ist es ein Quadrat.
Eine übersichtliche Einordnung des symmetrischen Trapezes findest du im Artikel zum Haus der Vierecke.
Symmetrieeigenschaften
Punktsymmetrie
Ein symmetrisches Trapez ist im Allgemeinen nicht punktsymmetrisch.
Ausnahmen:
Wenn ein symmetrisches Trapez ein Rechteck (oder ein Quadrat als Spezialfall des Rechtecks) ist, ist es punktsymmetrisch zum Schnittpunkt der Diagonalen.
Achsensymmetrie
Ein symmetrisches Trapez ist immer achsensymmetrisch, Symmetrieachse ist die Mittelsenkrechte der beiden parallelen Seiten.
Umkreis und Inkreis
Umkreis
Ein symmetrisches Trapez hat immer einen Umkreis.
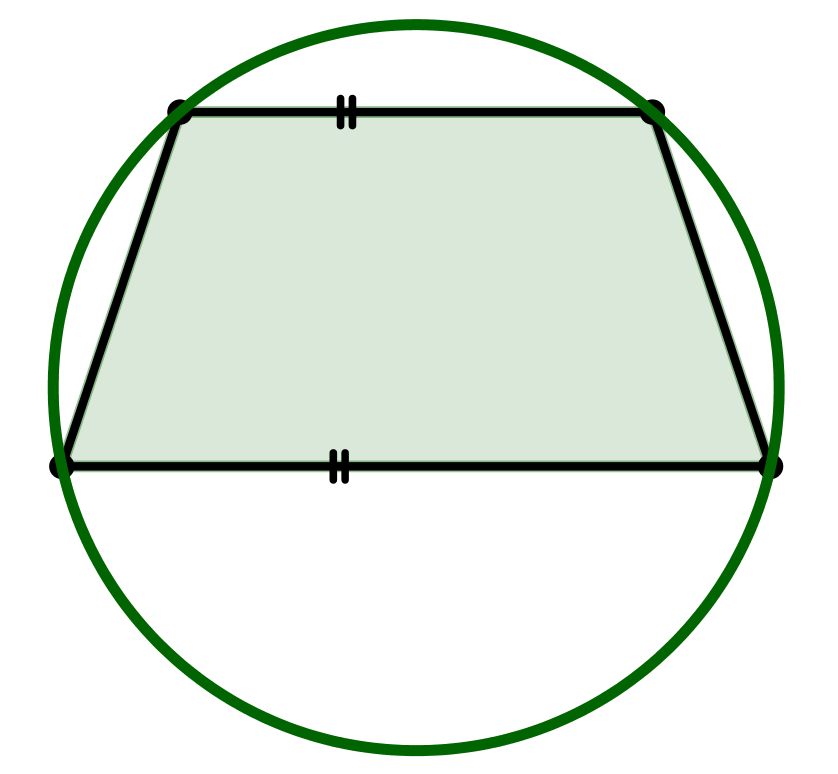
Umkreis eines symmetrischen Trapezes
Kein Inkreis
Ein symmetrisches Trapez hat im Allgemeinen keinen Inkreis. Es gibt aber Ausnahmen, zum Beispiel, wenn das symmetrische Trapez ein Quadrat ist.
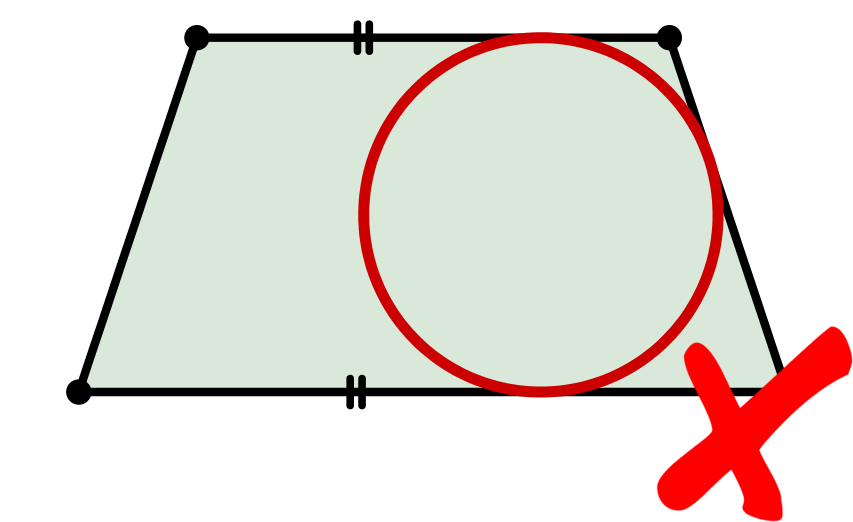
Kein Inkreis eines symmetrischen Trapezes
Flächeninhalt und Umfang
Flächeninhalt
Die Fläche eines symmetrischen Trapezes ist das Produkt von Höhe und der halben Summe der beiden zueinander parallelen Seiten:
Wenn man ein symmetrisches Trapez verdoppelt und das Zweite um 180° gedreht an das Erste legt, entsteht ein Parallelogramm mit der Grundlinie (a+c). Durch das Anwenden der Flächenformel eines Parallelogramms erhält man die oben genannte Formel.
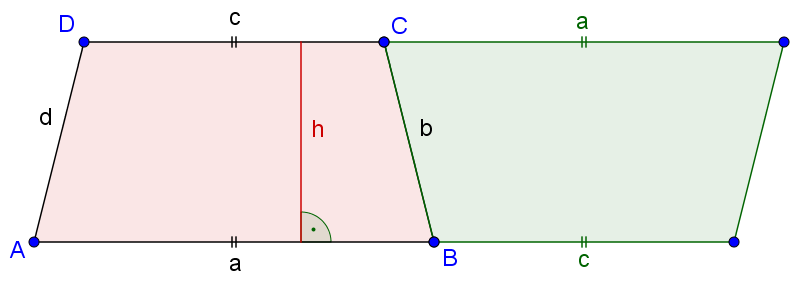
Umfang
Der Umfang eines symmetrischen Trapezes ist die Summe der Seitenlängen. Da die beiden Schenkel die gleiche Länge haben, ist der Umfang gegeben durch
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
