Eine Figur heißt achsensymmetrisch, wenn sie durch die Achsenspiegelung an ihrer/n Symmetrieachse(n) auf sich selbst abgebildet wird. Die Symmetrieachse kann dabei auch als Faltkante gesehen werden, durch die die Figur in zwei deckungsgleiche Stücke aufgeteilt wird.
Anstelle von "Achsensymmetrie" verwendet man auch den Begriff "Spiegelsymmetrie". Dabei stellt man sich die Symmetrieachse wie einen Spiegel vor.
Achsensymmetrie im Alltag

Achsensymmetrische Figuren
Quadrat
Jedes Quadrat hat vier Symmetrieachsen

Rechteck
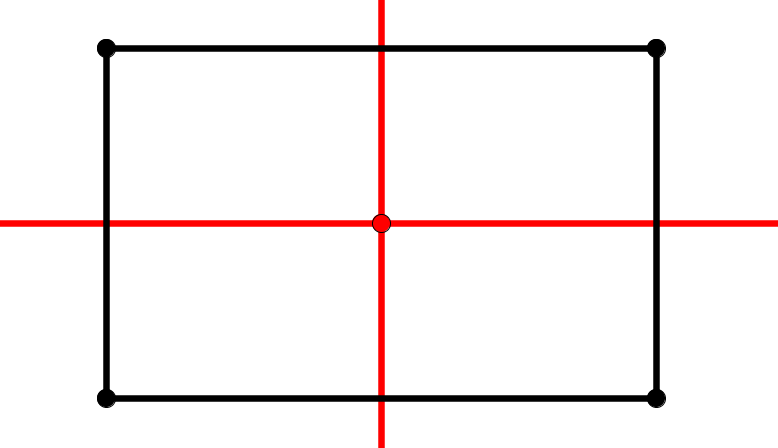
Ein Rechteck, das kein Quadrat ist, hat zwei Symmetrieachsen.
Raute
Eine Raute, die kein Quadrat ist, hat zwei Symmetrieachsen.

Drachenviereck
Ein Drachenviereck, das keine Raute ist, hat eine Symmetrieachse.

Symmetrisches Trapez
Ein symmetrisches Trapez, das kein Rechteck ist, hat eine Symmetrieachse.

Gleichseitiges Dreieck
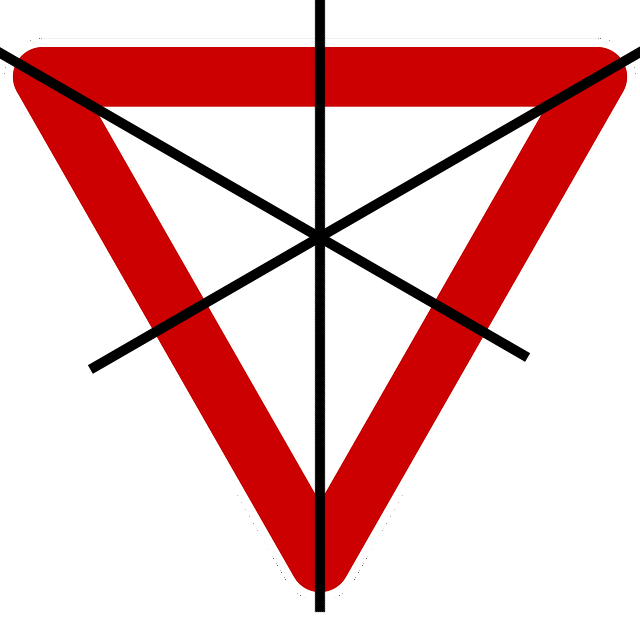
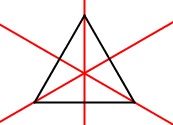
Ein gleichseitiges Dreieck hat drei Symmetrieachsen, die sowohl die Mittelsenkrechten als auch die Seitenhalbierenden sind.
Gleichschenkliges Dreieck
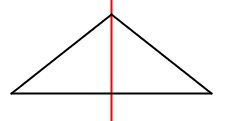
Ein gleichschenkliges Dreieck, das kein gleichseitiges Dreieck ist hat eine Symmetrieachse
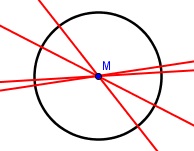
Kreis
Ein Kreis hat unendlich viele Symmetrieachsen durch den Ursprung.
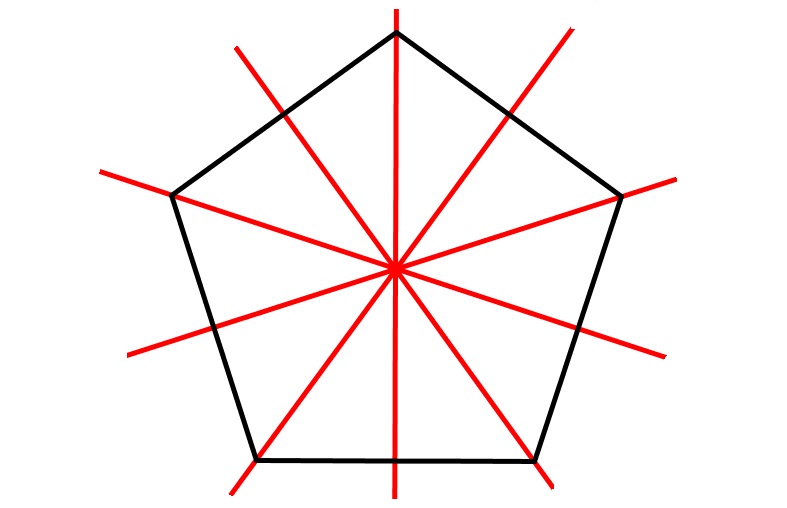
Regelmäßiges Fünfeck
Ein regelmäßiges Fünfeck hat fünf Symmetrieachsen
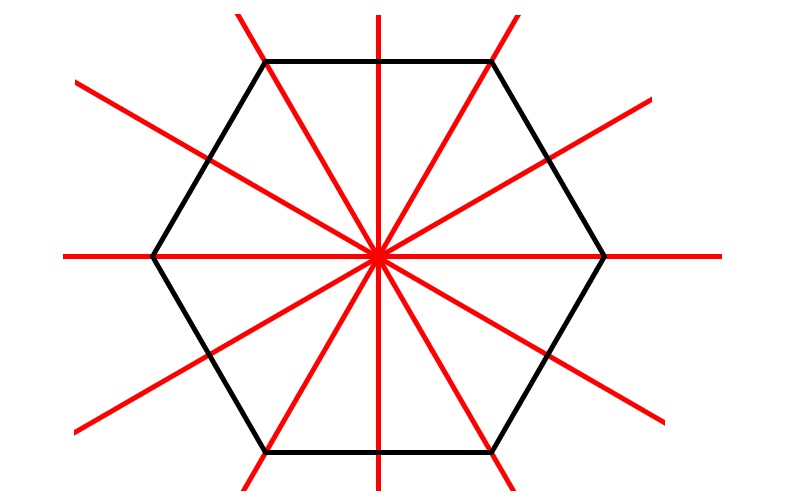
Regelmäßiges Sechseck
Ein regelmäßiges Sechseck hat sechs Symmetrieachsen
Beliebige Form
Diese Form hat eine Symmetrieachse, manche Figuren können auch gar keine, oder auch mehrere Symmetrieachsen haben.

Achsensymmetrie bei Funktionen
Mehr dazu im Artikel Achsensymmetrie von Funktionen.
Spiegeln an Achse
Wie man eine Figur spiegelt, findet man hier.
Videos zum Thema Achsenspiegelung
Laden
Laden
Quellenangaben:
Abb. 1: Autor: Thomas Henz. Quelle: Wikipedia
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
