Um die Länge einer Strecke im Koordinatensystem zu berechnen, sollte man zuerst einmal ihre Lage zu den Achsen bestimmen.
Parallel zur y-Achse
Man hat hier die y-Koordinate des unteren Punktes von der y-Koordinate des oberen Punktes subtrahiert.
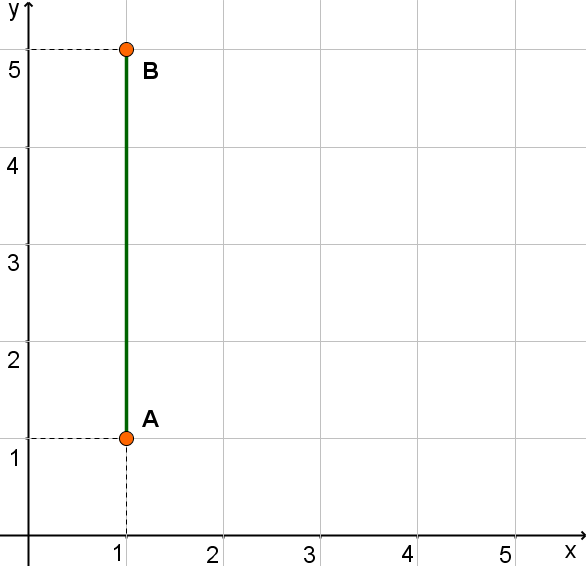
Sei B der obere Punkt:
Parallel zur x-Achse
Hier subtrahiert man die x-Koordinate des linken Punktes von der x-Koordinate des rechten Punktes.
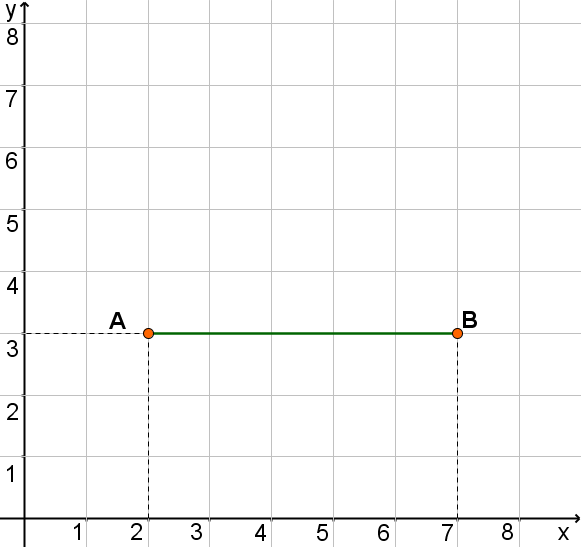
Sei der rechte Punkt:
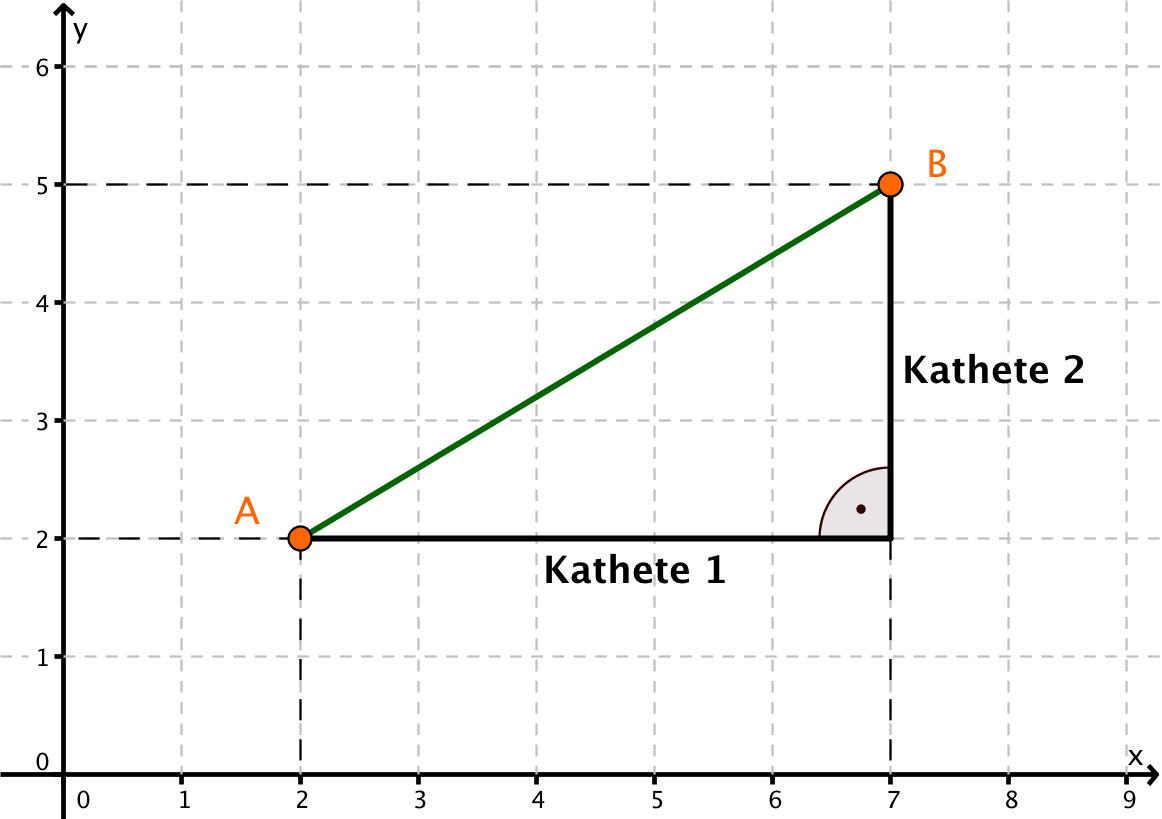
Sonstige Lagen
Hier verwendet man nun den Satz des Pythagoras:
Man berechnet die Kathetenlängen:
Nun verwendet man den Satz des Pythagoras, um die Hypotenuse zu berechnen:
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Berechnung von Längen im Koordinatensystem
