Mehr Abiturientinnen als Abiturienten:
52,4% der 244600 Jugendlichen, die am Ende des vergangenen Schuljahres ihre Schule mit der allgemeinen Hochschulreife verließen, waren Frauen. In den neuen Ländern und in Berlin liegt der Frauenanteil mit 59,1% deutlich höher als im früheren Bundesgebiet (50,8%).
Stellen Sie eine 4-Feldtafel auf, die diesen Sachzusammenhang beschreibt.
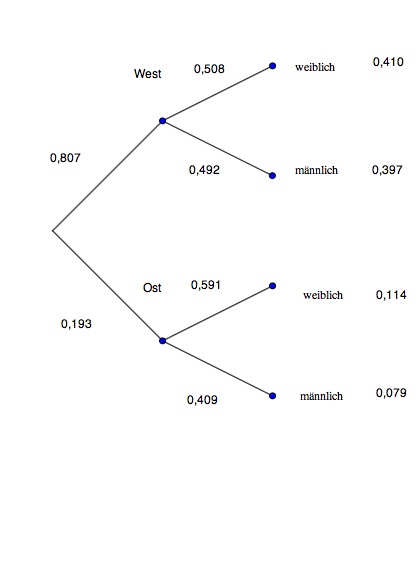
Zeichnen Sie ein Baumdiagramm mit dem 1. Merkmal "Herkunft" (Ost, West) und dem 2. Merkmal "Geschlecht" (männlich, weiblich).
Zeichnen Sie ein Baumdiagramm mit dem 1. Merkmal "Geschlecht" (männlich, weiblich) und dem 2. Merkmal "Herkunft" (Ost, West).
Aus der Gesamtheit aller Abiturientinnen und Abiturienten des betrachteten Jahrgangs wurde eine Person zufällig ausgewählt.
(1) Mit welcher Wahrscheinlichkeit stammt diese Person aus Ostdeutschland?
(2) Mit welcher Wahrscheinlichkeit ist die ausgewählte Person eine Frau?
(3) Falls diese Person aus Ostdeutschland kommt, mit welcher Wahrscheinlichkeit ist dies ein Mann?
(4) Falls diese Person eine Frau ist, mit welcher Wahrscheinlichkeit stammt sie aus Westdeutschland?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann → Was bedeutet das?