Das Baumdiagramm ist ein praktisches Hilfsmittel, um die verschiedenen möglichen Ergebnisse eines Zufallsexperiments übersichtlich aufzuschreiben.
Verwendet wird es sinnvollerweise dann, wenn ein Experiment aus mehreren Schritten besteht (wie zum Beispiel das Werfen einer Münze und danach eines Würfels, oder das mehrmalige Werfen einer Münze o.ä.).
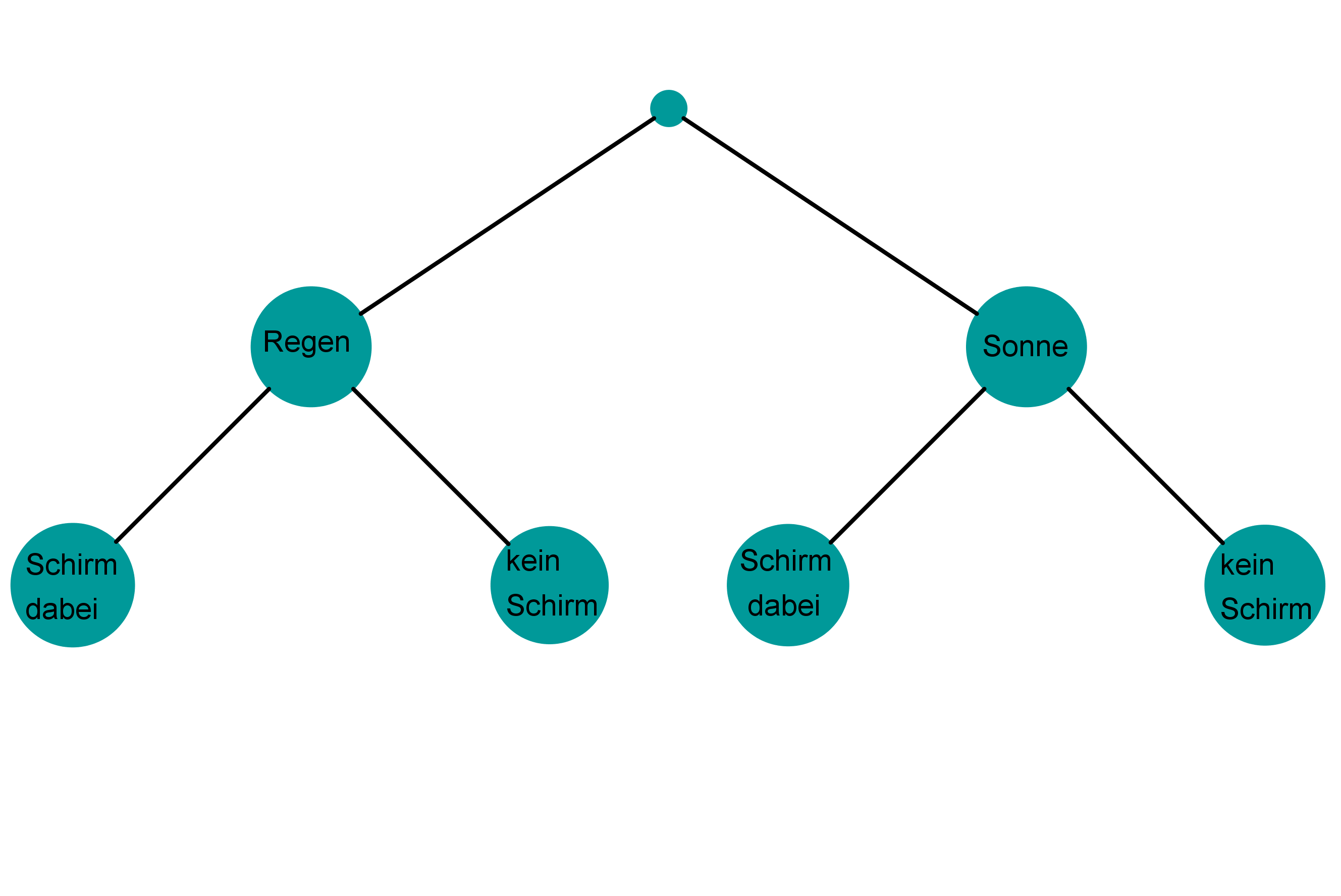
Bei einem solchen mehrstufigen (oder zusammengesetzten) Zufallsexperiment kann man mit einem Baumdiagramm
die Ergebnisse des zusammengesetzten Experiments
und die Wahrscheinlichkeiten dieser Ergebnisse
aus den Ergebnissen bzw. Wahrscheinlichkeitsverteilungen der Einzelexperimente ermitteln.
Vom Zufallsexperiment zum Baumdiagramm
Oft ist es nicht so einfach, von einer Sachsituation zu einem Baumdiagramm zu kommen. Deshalb hier ein paar Tipps:
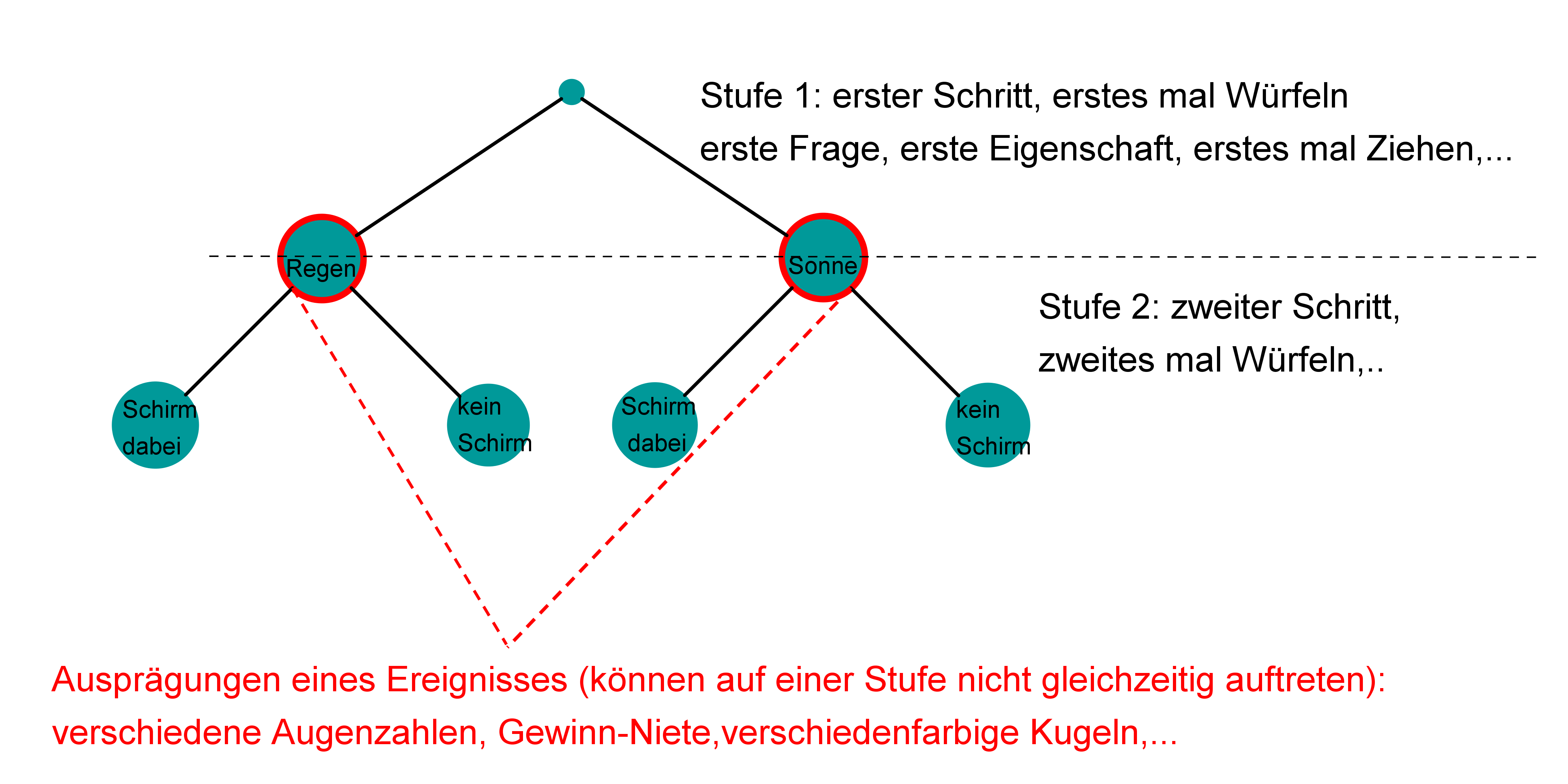
Überlege dir, was die Stufen in deinem Baum sind und was die Ereignisausprägungen.
Die Stufen sind zum Beispiel aufeinanderfolgende Handlungen (1./2./3. Würfelwurf, mehrmals Ziehen,…) oder Entscheidungen (erst wählt man eine Tür, dann eine Kiste,…).
Die Ereignisausprägungen sind die verschiedenen Möglichkeiten, die sich gegenseitig ausschließen (Augenzahlen beim Würfel, Kugelfarben, Antwortmöglichkeiten bei Fragen,…)
Pfad
Der Pfad im Baum entspricht einem Weg durch den Baum. Dabei startet man immer ganz oben am Start und geht (bis auf wenige Ausnahmen) auch bis zur untersten Stufe.
Würfelt man zum Beispiel dreimal, dann entspricht jedes mögliche Ergebnis (zum Beispiel 123, 541,…) einem Pfad.
Im Artikel Abzählen mit dem Baumdiagramm kann man nachlesen, wie ein Baumdiagramm verwendet werden kann, um die Anzahl der verschiedenen Ergebnisse zu bekommen. Möchte man mehr über die Wahrscheinlichkeiten wissen, so benötigt man oft die Pfadregeln.
Video zum Baumdiagramm und zu den Pfadregeln
Laden
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Baumdiagramm
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
