Überprüfung der Symmetrie

$g(x)=x^2\cdot \sin (x)g(x)=x^2\backslash cdot\backslash sin(x)$

Setze für jedes $xx$ jetzt $-x-x$ ein und überprüfe, ob die Gleichung $g(-x)=-g(x)g(-x)=-g(x)$ erfüllt ist, dann ist die Punktsymmetrie gegeben.

$g(-x)=(-x{)}^2\cdot sin(-x)g(-x)=(-x)^2\backslash cdot\; sin(-x)$

Da der Sinus punktsymmetrisch ist, kannst du das Minus in der Klammer nach außen ziehen.

$g(-x)=-x^2\cdot sin(x)=-g(x)g(-x)=-x^2\backslash cdot\; sin(x)=-g(x)$

Damit ist die Punktsymmetrie bestätigt.

Berechnung des Integrals

${\int }_{-\pi }^{\pi }{x}^2\cdot sin(x)\text{d}x\backslash int\_\{-\backslash pi\}^\{\backslash pi\}\{x^2\backslash cdot\; sin(x)\}\backslash text\{d\}x$

Du hast gerade ausgerechnet, dass die Funktion punktsymmetrisch ist. Dazu kommt noch, dass du zwei Grenzen hast, die gleichweit vom Ursprung entfernt sind. Das sagt dir, dass die Flächen von $-\pi -\backslash pi$ bis $00$ und von $00$ bis $\pi \backslash pi$ den gleichen Betrag haben. Wenn du sie jetzt voneinander abziehst, ist der Wert deines Integrals einfach $00$.

Aufgrund von Punktsymmetrie und gleichen Betragsgrenzen gilt:

${\int }_{-\pi }^{\pi }{x}^2\cdot sin(x)\text{d}x=0\backslash int\_\{-\backslash pi\}^\{\backslash pi\}\{x^2\backslash cdot\; sin(x)\}\backslash text\{d\}x=0$

$33$ Skizzieren Sie im Bereich $-1\le x\le 4-1\backslash leq\; x\backslash leq4$ den Graphen einer in $\mathbb{R}\backslash mathbb\{R\}$ definierten Funktion $ff$ mit den folgenden Eigenschaften:

• $ff$ ist nur an der Stelle $x=3x=3$ nicht differenzierbar.

• $f(0)=2f(0)=2$ und für die Ableitung $f^{\mathrm{\prime }}f\text{'}$ von $ff$ gilt: $f^{\mathrm{\prime }}(0)=-1f\text{'}(0)=-1$

• Der Graph von $ff$ ist im Bereich linksgekrümmt.

(3 BE)

Skizzieren des Graphen

• Zeichne den gegebenen Punkt ein.

• Zeichne die Tangente/Gerade im Punkt $(0\mathrm{\mid }2)(0|2)$ mit der Steigung $-1-1$.

• Überlege dir, was es heißt, dass bei $x=3x=3$ die Funktion nicht differenzierbar ist. Hier muss also ein Loch oder ein Knick vorliegen.

• Was bedeutet die Linkskrümmung? Es muss also ein Minimum geben.

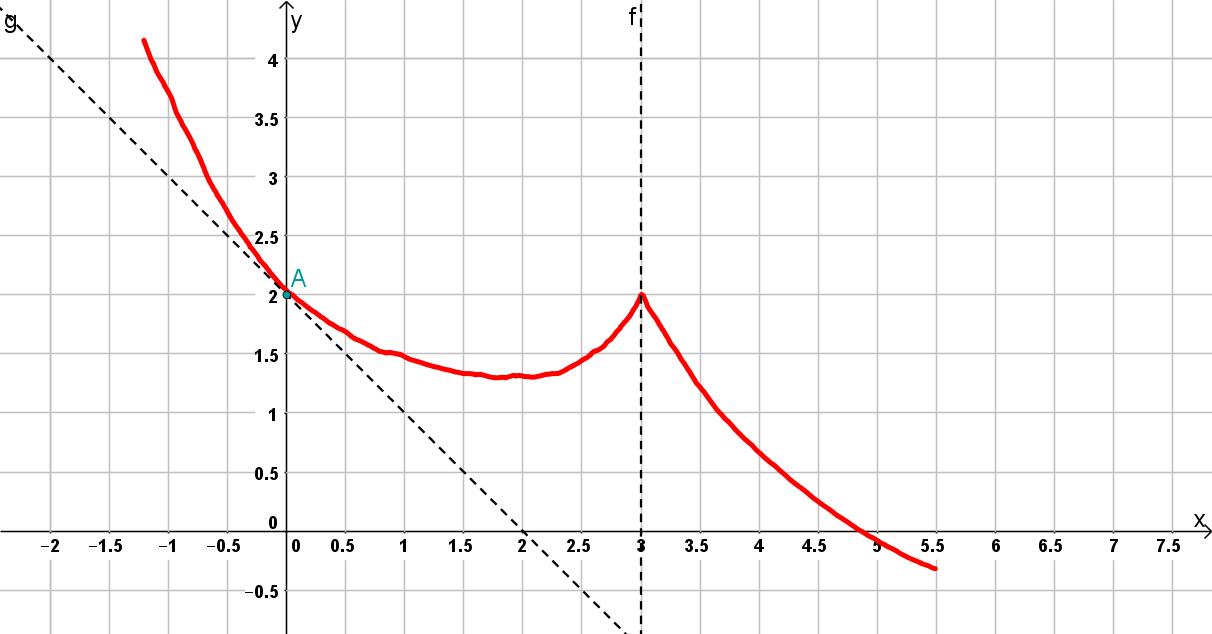
Es gibt natürlich mehrere Lösungen. Hier ist eine mögliche.

$44$ Gegeben ist eine in $\mathbb{R}\backslash mathbb\{R\}$ definierte ganzrationale Funktion $ff$ dritten Grades, deren Graph $G_{f}G\_f$ an der Stelle $x=1x=1$ einen Hochpunkt und an der Stelle $x=4x=4$ einen Tiefpunkt besitzt.

$a)a)$ Begründen Sie, dass der Graph der Ableitung $f^{\mathrm{\prime }}f\text{'}$ von $ff$ eine Parabel ist, welche die $xx$-Achse in den Punkten $(1\mathrm{\mid }0)(1|0)$ und $(4\mathrm{\mid }0)(4|0)$ schneidet und nach oben geöffnet ist. (3BE)

$b)b)$ Begründen Sie, dass $\mathrm{2,5}2\{,\}5$ die $xx$-Koordinate des Wendepunktes von $G_{f}G\_f$ ist. (2 BE)

Lösung Aufgabe $4a4a$

• Da die Funktion $ff$ den Grad $33$ hat, hat die Ableitung $f^{\mathrm{\prime }}f\text{'}$ den Grad $22$, ist also eine Parabel.

• Die Extrempunkte der Funktion $ff$ sind die Nullstellen der Ableitung $f^{\mathrm{\prime }}f\text{'}$, deswegen hat $f^{\mathrm{\prime }}f\text{'}$ die Nullstellen $(1\mathrm{\mid }0)(1|0)$ und $(4\mathrm{\mid }0)(4|0)$.

• Da der erste Extrempunkt der Funktion ein Hochpunkt ist, steigt der Graph erst und fällt dann, beim Tiefpunkt fällt er erst und steigt dann. Das überträgt sich auf die Ableitungsfunktion und den Graphen $G_{f^{\mathrm{\prime }}}G\_\{f\text{'}\}$. Dieser ist erst oberhalb der $xx$-Achse vor der ersten Nullstelle, zwischen den Nullstellen unterhalb der $xx$-Achse und nach der zweiten Nullstelle wieder oberhalb der $xx$-Achse. Deswegen liegt eine nach oben geöffnete Parabel vor.

Lösung Aufgabe $4b4b$

Der Hochpunkt und der Tiefpunkt sind auf der $xx$-Achse $33$ Längeneinheiten auseinander. Genau in der Mitte von einem Hoch und einem Tiefpunkt bei einer ganzrationalen Funktion ist der Wendepunkt. Daraus folgt, dass der Wendepunkt genau in der Mitte zwischen $11$ und $44$ liegen muss, also bei $\mathrm{2,5}2\{,\}5$.

$55$ Diese Abbildung zeigt den Graphen der in $\mathbb{R}\backslash mathbb\{R\}$ definierten Funktion $ff$.

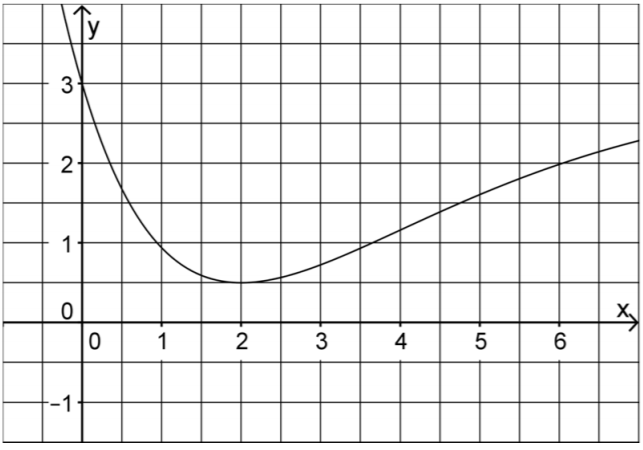
$a)a)$ Bestimmen Sie mithilfe der Abbildung eine Näherungswert für ${\int }_3^{5}f(x)\text{d}x\backslash int\_3^5\{f(x)\backslash text\{d\}\}x$. (2 BE)

Die Funktion $FF$ ist die in $\mathbb{R}\backslash mathbb\{R\}$ definierte Stammfunktion von $ff$ mit $F(3)=0F(3)=0$.

$b)b)$ Geben Sie mit Hilfe der Abbildung einen Näherungswert für die Ableitung von $FF$ an der Stelle $x=2x=2$ an. (1 BE)

$c)c)$ Zeigen Sie, dass $F(b)={\int }_3^{b}f(x)\text{d}xF(b)=\backslash int\_3^b\{f(x)\backslash text\{d\}\}x$ mit $b\in \mathbb{R}b\; \backslash in\; \backslash mathbb\{R\}$ gilt. (2 BE)

Lösung Aufgabe $5a5a$

Die Größe des Integrals kannst du einfach ablesen, da eine Vorstellung zum Integral die Fläche unter der Kurve ist.

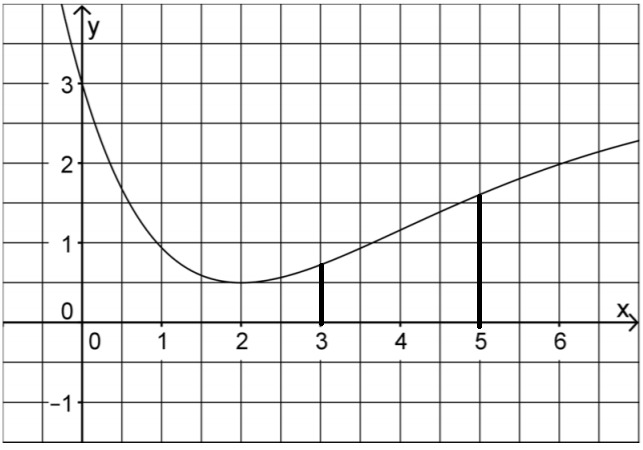
Zähle jetzt einfach die Kästchen, die von der Kurve, den zwei senkrechten Linien und der $xx$-Achse eingeschlossen sind. $44$ Kästchen zusammen geben eine Flächeneinheit ($1FE1\backslash ,\; FE$).

${\int }_3^{5}f(x)\text{d}x\approx 9K\ddot{a}stchen=\mathrm{2,25}FE\backslash int\_3^5\{f(x)\backslash text\{d\}\}x\backslash approx\; 9\; Kästchen\; =\; 2\{,\}25\; FE$

Ob du $99$ oder $1010$ Kästchen heraus bekommst, ist bei einem Näherungswert nicht wichtig. Punkte gibt es trotzdem ;).

Lösung Aufgabe $5b5b$

Die Aufgabe ist einfach nur gemein gestellt und klingt total kompliziert. Ist es aber wirklich nicht! Was ist denn die Ableitung von der Stammfunktion $FF$? Genau, einfach die Funktion $ff$. Deswegen musst du beim ablesen von diesem Punkt einfach nur in der Abbildung, die du schon gegeben hast, den Punkt mit der $xx$-Koordinate $22$ heraus suchen.

Bei $x=2x=2$ ist $y=\mathrm{0,5}y=0\{,\}5$ da die Funktion $ff$ die Ableitung der Stammfunktion $FF$ ist.

Lösung Aufgabe $5c5c$

Überlege dir, wie du die Funktion $ff$ integrierst. Dazu benötigst du die Stammfunktion. Diese hast du schon gegeben. Außerdem weißt du schon, dass $F(3)=0F(3)=0$. Aus dem Hauptsatz der Differential und Integralrechnung folgt:

${\int }_a^{b}f(x)\text{d}x=F(b)-F(a)\backslash int\_a^b\{f(x)\backslash text\{d\}\}x=F(b)-F(a)$

Setze die gegebenen Grenzen aus der Aufgabenstellung ein.

${\int }_3^{b}f(x)\text{d}x=F(b)-F(3)\backslash int\_3^b\{f(x)\backslash text\{d\}\}x=F(b)-F(3)$

Setze ein, was du schon weißt.

${\int }_3^{b}f(x)\text{d}x=F(b)-0=F(b)\backslash int\_3^b\{f(x)\backslash text\{d\}\}x=F(b)-0=F(b)$

Und schon bist du fertig! :)