Aufgaben zum Monotonieverhalten

Bestimme das Monotonieverhalten der nachfolgenden Funktionen.

$f\left(x\right)=x^3-3x^2-24x+6$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonieverhalten berechnen

Variante 1

$\displaystyle f\left(x\right)$	$=$	$\displaystyle x^3-3x^2-24x+6$
	↓	Die Funktion $f$ ist ein Polynom und daher (beliebig oft) differenzierbar. Du kannst daher die erste Ableitung von $f$ berechnen um das Monotonieverhalten zu bestimmen.
$\displaystyle f´\left(x\right)$	$=$	$\displaystyle 3x^2-6x-24$
	↓	Die erste Ableitung ist also erneut ein Polynom. Berechne nun die Nullstellen von $f^{'}$ .
$\displaystyle f´\left(x\right)$	$=$	$\displaystyle 3\cdot\left(x^2-2x-8\right)$
$\displaystyle f´\left(x\right)$	$=$	$\displaystyle 0$
	↓	Setze die Funktionsgleichung von $f^{'}$ ein.

$\Leftrightarrow 3\cdot\left(x^2-2x-8\right)=0$

Teile beide Seiten der Gleichung durch $3$ .

$\Leftrightarrow x^2-2x-8=0$

Die linke Gleichungsseite ist durch ein Polynom zweiten Grades gegeben. Es hat also höchstens zwei reelle Nullstellen. Durch Anwendung der p-q-Formel erhältst du

\displaystyle \def\arraystretch{1.25} \begin{aligned}x&=\frac22 \pm \sqrt{(\frac22)^2 - (-8)}\\&= 1 \pm \sqrt{1+8}\\&=1 \pm \sqrt{9}\\&=1 \pm 3\in \{-2, 4\}\end{aligned}

Dies sind zwei reelle Nullstellen und daher genau die Lösungen der Gleichung.

$\Leftrightarrow x \in \{-2, 4\}$

Da $f^{'}$ nur diese Nullstellen hat und als Polynom insbesondere reellwertig, auf ganz $\mathbb{R}$ definiert und stetig ist, kannst du den Zwischenwertsatz verwenden.

Betrachte die Intervalle

$I_1 = ]- \infty, -2[=\{x \in \mathbb{R} | x < -2\}$

$I_2 = ]-2, 4[=\{x \in \mathbb{R} | -2 < x < 4\}$

$I_3 = ]4, +\infty[=\{x \in \mathbb{R}|x > 4\}$ ,

die zwischen den Nullstellen von $f^{'}$ liegen.

Wähle beispielsweise

$x_1=-3 \in I_1$

$x_2=3 \in I_2$

$x_3=5\in I_3$

Setze diese in $f^{'}$ ein.

$f'(x_1)=f'(-3)=3\cdot\left((-3)^2-2\cdot(-3)-8\right)=3\cdot(9+6-8)=3 \cdot 7 = 21>0$

$f'(x_2)=f'(3)=3\cdot\left(3^2-2\cdot3-8\right)=3\cdot(9-6-8)=3 \cdot (-5) = -15<0$

$f'(x_3)=f'(5)=3\cdot\left(5^2-2\cdot5-8\right)=3\cdot(25-10-8)=3 \cdot 7 = 21>0$

Somit gilt $f'(x) \begin{cases}>0 : x \in \text{ } ]-\infty, -2[\\<0 : x \in \text{ } ]-2{,}4[ \\>0 : x \in \text{ } ]4,+\infty[ \\ =0: \text{sonst}\end{cases}$

womit $G_{f}$ auf $]-\infty, -2]$ und $[4,+\infty[$ streng monoton wächst, sowie auf $[- 2,4]$ streng monoton fällt.

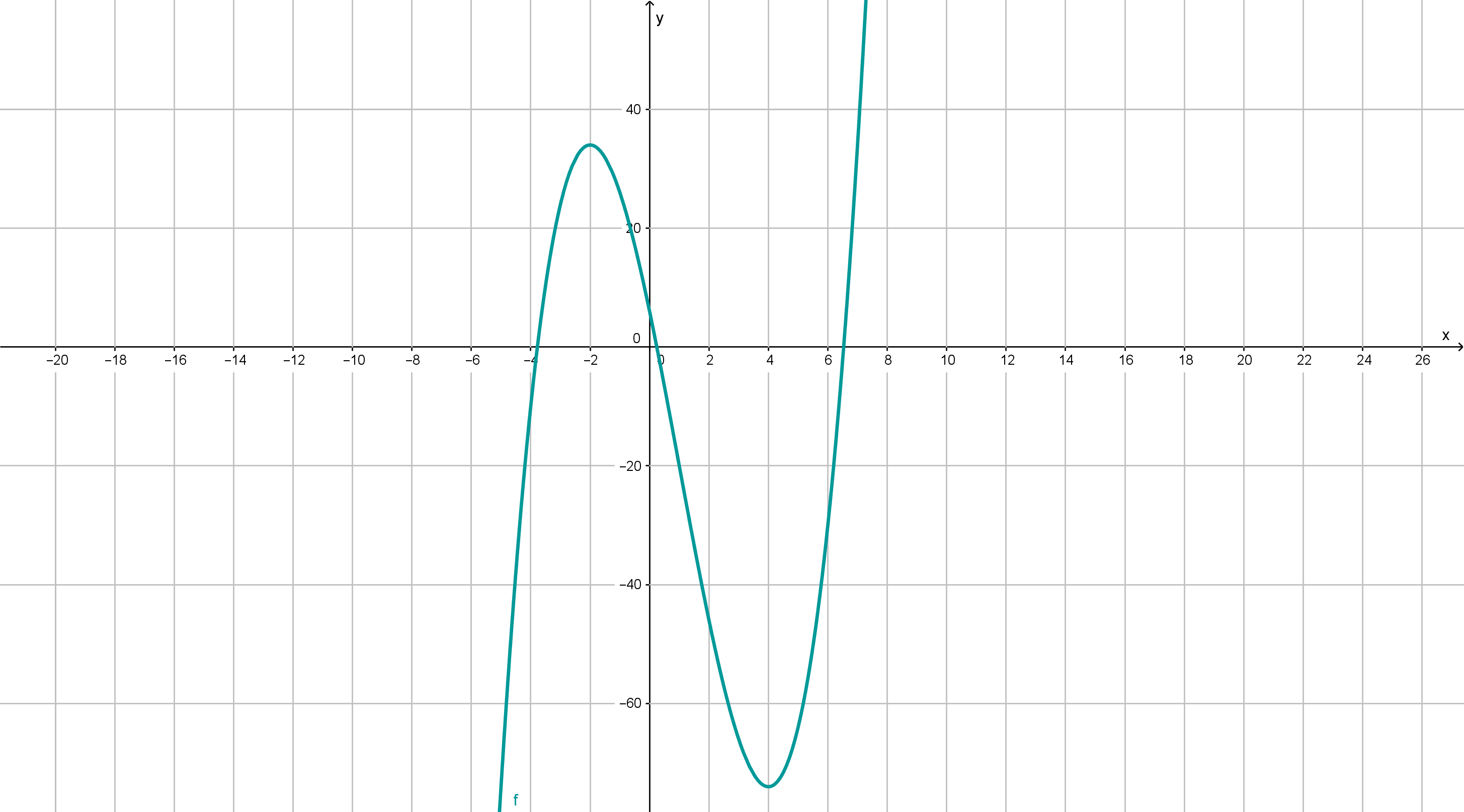
Variante 2

Bildung der ersten Ableitung:

\displaystyle f'(x)=3x^2-6x-24

\displaystyle f'(x)=0\Leftrightarrow3x^2-6x-24=0

\displaystyle \Leftrightarrow x^2-2x-8=0\Leftrightarrow\left(x+2\right)\cdot\left(x-4\right)=0\Leftrightarrow x_1=-2\vee x_2=-24

Der Graph der vorzeichengleichen Funktion ist eine nach oben geöffnete Parabel mit den genannten Nullstellen.Links von der Nullstelle

\displaystyle x_1-2

liegt der Graph oberhalb der x-Achse. Das bedeutet, dass f' in diesem Bereich positiv ist und der Graph von f im Intervall

\displaystyle \left(-\infty,-2\right)

wachsend und im Intervall

\displaystyle \left(-2{,}4\right)

liegt der Graph von f' unterhalb der x-Achse und somit ist f' dort negativ und f fällt.Rechts von x=4 wächst die Funktion dann wieder.Somit liegt an der Stelle

\displaystyle x_1=-2

ein Maximum und an der Stelle

\displaystyle x_1=4

ein Minimum.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

$f\left(x\right)=3x^4+8x^3-48x^2+3$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonieverhalten berechnen

$f\left(x\right)=3x^4+8x^3-48x^2+3$

Die Funktion $f$ ist ein Polynom und daher (beliebig oft) differenzierbar. Du kannst also die erste Ableitung von $f$ berechnen, um das Monotonieverhalten zu bestimmen.

$\displaystyle f'(x)$	$=$	$\displaystyle 12x^3+24x^2-96x$
	$=$	$\displaystyle 12x\cdot(x^2+2x-8)$

Die erste Ableitung ist also erneut ein Polynom.

Berechne nun die Nullstellen von $f^{'}$ .

$f^{'} (x) = 0$

Setze die Funktionsgleichung von $f^{'}$ ein.

$\Leftrightarrow 12x \cdot (x^2+2x-8)=0$

Teile beide Seiten der Gleichung durch $12$ .

$\Leftrightarrow x \cdot (x^2+2x-8) = 0$

Die linke Gleichungsseite ist durch ein Polynom dritten Grades gegeben. Es hat also höchstens drei reelle Nullstellen.

Die linke Seite der Gleichung ist genau dann gleich $0$ , wenn mindestens einer der beiden Faktoren gleich $0$ ist. Dadurch kannst du sofort die Nullstelle bei $x = 0$ ablesen.

Im zweiten Fall könnte $x^{2} + 2 x - 8$ gleich $0$ sein.

Durch Anwendung der Mitternachtsformel erhältst du

$\displaystyle x$	$=$	$\displaystyle -\frac22 \pm \sqrt{(\frac22)^2 - (-8)}$
	$=$	$\displaystyle -1 \pm \sqrt{1+8}$
	$=$	$\displaystyle -1 \pm \sqrt{9}$
	$=$	$\displaystyle -1 \pm 3 \in \{-4, 2\}$

Somit sind alle drei Nullstellen von $f^{'}$ reell.

$\Leftrightarrow x \in \{-4, 0, 2\}$

Da $f^{'}$ nur diese Nullstellen hat und als Polynom insbesondere reellwertig, auf ganz $\mathbb{R}$ definiert und stetig ist, kannst du den Zwischenwertsatz verwenden.

Betrachte die Intervalle

$I_1 = ]- \infty, -4[=\{x \in \mathbb{R} | x < -4\}$

$I_2 = ]-4, 0[=\{x \in \mathbb{R} | -4 < x < 0\}$

$I_3 = ]0{,}2[ = \{x \in \mathbb{R} | 0 < x < 2\}$

$I_4 = ]2, +\infty[=\{x \in \mathbb{R} | x > 2\}$ ,

die zwischen den Nullstellen von $f^{'}$ liegen.

Wähle beispielsweise

$x_1=-5 \in I_1$

$x_2=-1 \in I_2$

$x_3=1 \in I_3$

$x_4=3\in I_4$

Setze diese in $f^{'}$ ein.

$f'(x_1)=f'(-5)=12\cdot(-5) \cdot ((-5)^2+2(-5)-8)=\underbrace{(-60)}_{<0}\cdot\underbrace{(25-18)}_{>0}<0$

$f'(x_2)=f'(-1)=12\cdot(-1) \cdot ((-1)^2+2\cdot(-1)-8)=\underbrace{(-12)}_{<0}\cdot\underbrace{(1-2-8)}_{<0}>0$

$f'(x_3)=f'(1)=12\cdot(1+2-8)=12\cdot(-5)=-60<0$

$f'(x_4)=f'(3)=12\cdot 3\cdot (3^2+2\cdot 3-8)=36\cdot (9+6-8)=36\cdot 7>0$

Somit gilt $f'(x) \begin{cases}<0 : x \in \text{ } ]-\infty, -4[\\>0 : x \in \text{ } ]-4{,}0[ \\<0 : x \in \text{ } ]0{,}2[ \\ >0 : x \in \text{ } ]2, +\infty[ \\ =0: \text{sonst}\end{cases}$

womit $G_{f}$ auf $[- 4,0]$ und $[2, +\infty[$ streng monoton wächst, sowie auf $]-\infty, -4]$ und $[0,2]$ streng monoton fällt.

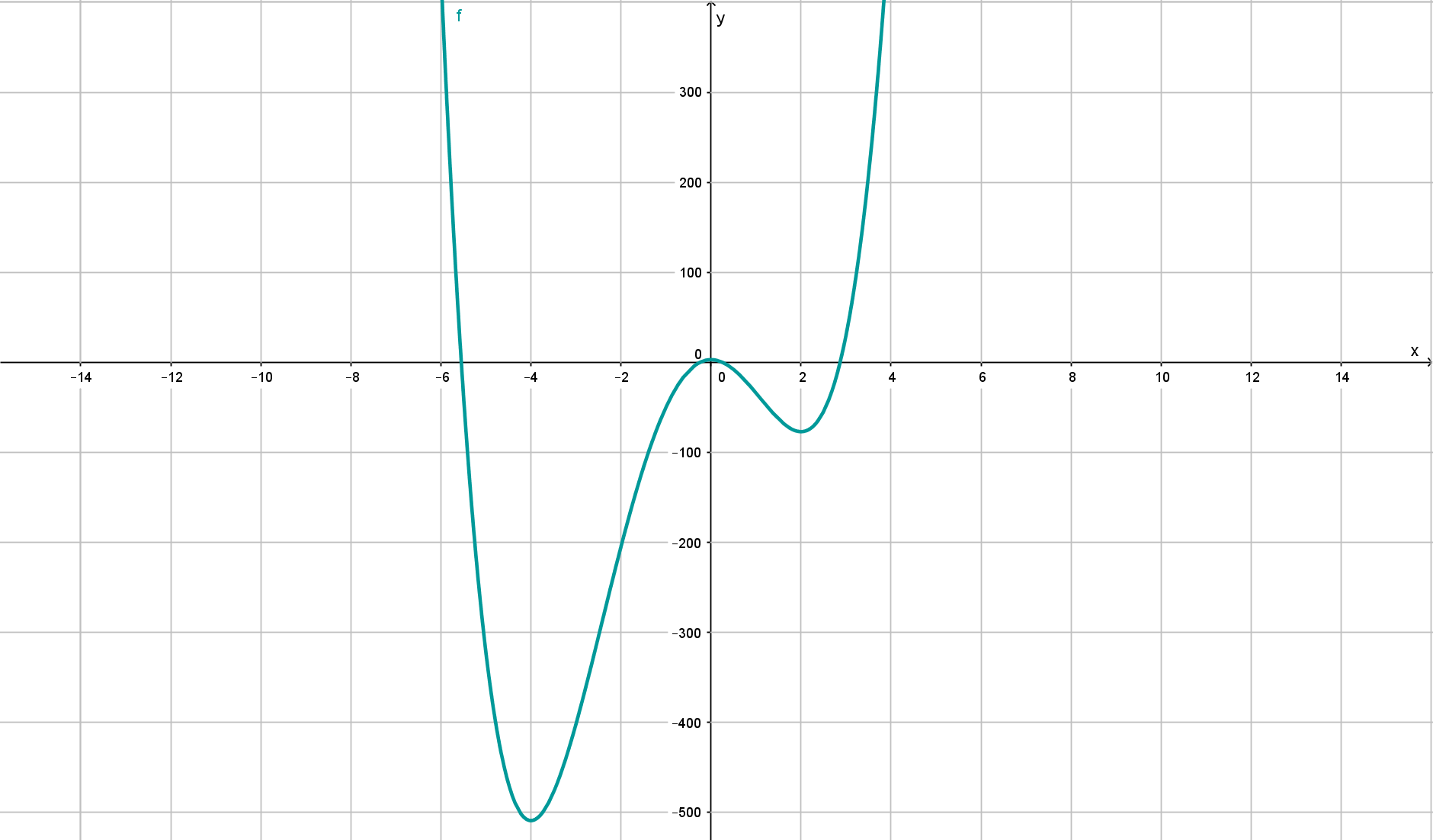
Anmerkung zum obigen Bild

In diesem Bild, sieht es so aus, als ob die Funktion durch den Wert $0$ geht. Das ist aber hier nur der Fall, weil zu weit reingezoomt wurde, damit man die gesamte Funktion, insbesondere das Minimum bei $x = - 4$ sieht ;) Daher folgt nochmal ein Bild von der Funktion ohne den unteren Part mit dem Minimum bei $x = - 4$ :

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

$f\left(x\right)=\dfrac{2x^2}{2x-1}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonieverhalten berechnen
$f\left(x\right)=\frac{2x^2}{2x-1}$
Die Funktion $f$ ist ein Quotient zweier Polyonme, du kannst daher die erste Ableitung mit der Quotientenregel berechnen um das Monotonieverhalten zu bestimmen.
$f'\left(x\right)=\frac{4x\cdot\left(2x-1\right)-2x^2\cdot2}{\left(2x-1\right)^2}$ $=\frac{8x^2-4x-4x^2}{\left(2x-1\right)^2}=\frac{4x^2-4x}{\left(2x-1\right)^2}$
Nullstelle von $\mathrm f'\left(\mathrm x\right)$ (also Extrema von $f\left(x\right)$ ) berechnen: $\mathrm f'\left(\mathrm x\right)=0$
Die Nullstellen einer gebrochen rationalen Funktion sind gleichzeitig die Nullstellen des Zählers. $\mathrm f'\left(\mathrm x\right)=0\;\;\Leftrightarrow\;\;4x^2-4x=0$
Vereinfache diesen Ausdruck:
$4x^2-4x=4x\left(x-1\right)$
Nun kann man ganz leicht die Nullstellen der 1. Ableitung (die Extrema von $f\left(x\right)$ ) ablesen.
Hier wird nun der Weg mit der Monotonietabelle gewählt, da die 2. Ableitung relativ kompliziert ist. Man muss allerdings bei der Monotonietabelle die Polstellen der Funktion beachten.
$4x\left(x-1\right)=0\;\;\Leftrightarrow\;\;4x=0\;\text{oder}\;\left(x-1\right)=0$
$\Rightarrow$ $x_{1} = 0$ und $x_{2} = 1$
Berechnen der Polstelle . Suche also die Nullstellen des Nenners von $f\left(x\right)$ . (Übrigens haben $f\left(x\right)$ und $f'\left(x\right)$ immer dieselben Polstellen.)
$2 x - 1 = 0$
$2 x = 1$
$x_{Polstelle}=\frac12$
Faktorisiere nun die 1. Ableitung.
$f`\left(x\right)=\frac{4x\cdot\left(x-1\right)}{\left(2x-1\right)^2}$
Erstelle eine Vorzeichentabelle.
Achtung: Polstelle nicht vergessen!
Nun kann man aus der Vorzeichentabelle das Monotonieverhalten ganz einfach ablesen. Steht in der letzten Zeile ein Minus ist die Funktion in diesem Bereich streng monoton fallend, steht dort ein Plus ist die Funktion streng monoton steigend.
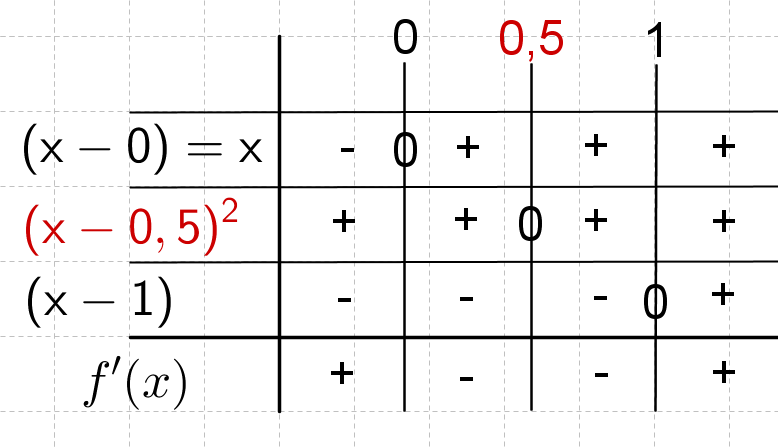
$\rbrack-\infty;0\rbrack$ : $\rightarrow G_f$ ist streng monoton steigend
$\lbrack0;\frac12\lbrack$ : $\;\;\;\;$ $\rightarrow G_f$ ist streng monoton fallend
$\rbrack\frac12;1\rbrack$ : $\;\;\;\;$ $\rightarrow G_f$ ist streng monoton fallend
$\lbrack1;\infty\lbrack:\;\;\;\;\;\rightarrow G_f$ ist streng monoton steigend
Achtung:
Man darf die beiden Intervalle $\lbrack0;\frac12\lbrack$ und $\rbrack\frac12;1\rbrack$ nicht zu einem Intervall $\lbrack0;1\rbrack$ zusammenlegen, da die Funktion und damit die Monotonie an dem Wert $\frac12$ nicht definiert ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇