Stammfunktion und Integral
Gegeben ist die Funktion mit .
Bestimmen Sie eine Stammfunktion von .
Gegeben ist die Funktion mit . Bestimmen Sie diejenige Stammfunktion von , deren Schaubild den Punkt enthält.
Zeigen Sie, dass eine Stammfunktion von ist.
Berechnen Sie das Integral .
Berechnen Sie das Integral .
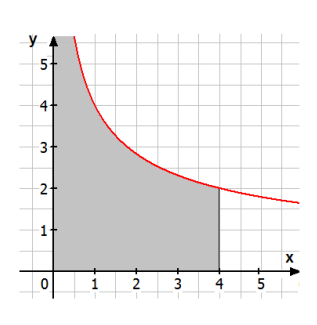
Die Funktion f mit schließt mit der x-Achse, der Geraden und der y-Achse eine nach oben offene Fläche ein (siehe Skizze). Untersuchen Sie, ob diese Fläche einen endlichen Flächeninhalt hat und bestimmen Sie diesen gegebenenfalls.
Dieses Werk steht unter der freien Lizenz
CC BY 4.0 mit Namensnennung Landesbildungsserver Baden-Württemberg → Was bedeutet das?
