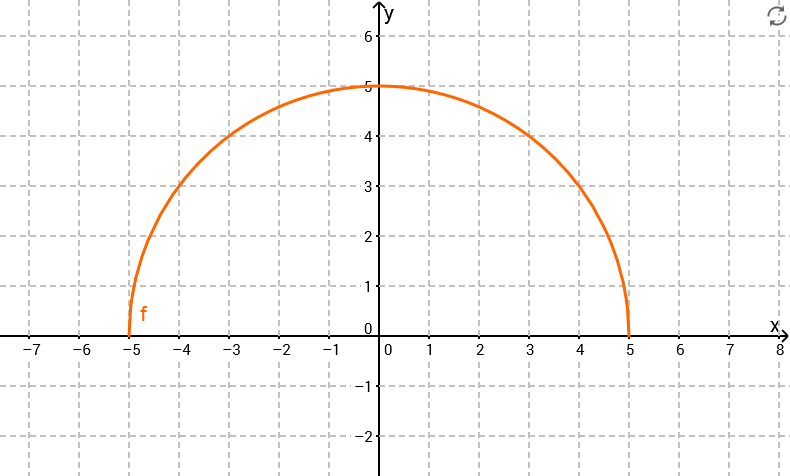
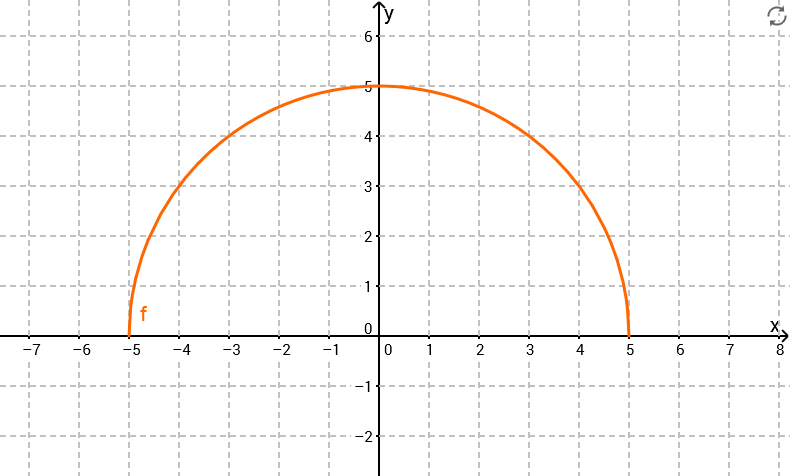
Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion mit Definitionsbereich .
Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte M den Abstand hat. Zeichnen Sie den Graphen von f in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: , ) und begründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist. (5 BE)
Betrachtet wird nun die Integralfunktion mit Definitionsbereich .
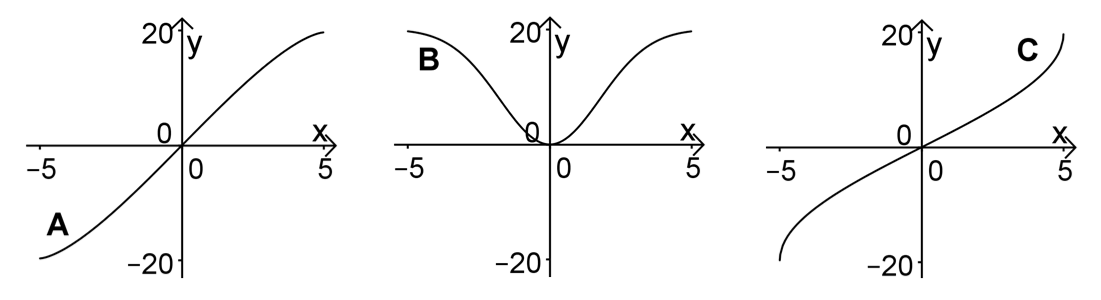
Zeigen Sie mithilfe einer geometrischen Überlegung, dass gilt. Einer der Graphen und ist der Graph von . Entscheiden Sie, welcher dies ist, und begründen Sie Ihre Entscheidung, indem Sie erklären, warum die beiden anderen Graphen nicht infrage kommen. (5 BE)
Berechnen Sie, um wie viel Prozent der Inhalt der Querschnittsfläche des Tunnels bei einer Modellierung mit von dem in Aufgabe 2a berechneten Wert abweicht. (2 BE)
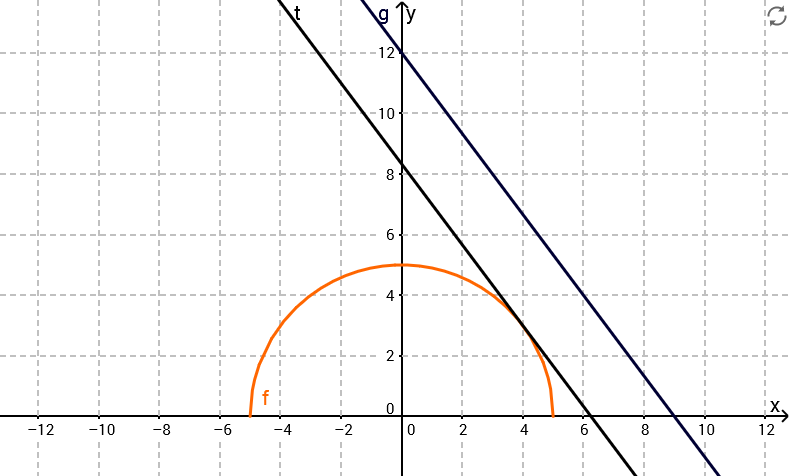
Der Tunnel soll durch einen Berg führen. Im betrachteten Querschnitt wird das Profil des Berghangs über dem Tunnel durch eine Gerade mit der Gleichung modelliert.
Zeigen Sie, dass die Tangente an den Graphen von im Punkt parallel zu verläuft. Zeichnen Sie und in das Koordinatensystem aus Aufgabe 3a ein. (4 BE)
Der Punkt aus Aufgabe 3d entspricht demjenigen Punkt der Tunnelwand, der im betrachteten Querschnitt vom Hangprofil den kleinsten Abstand in Metern hat. Beschreiben Sie die wesentlichen Schritte eines Verfahrens zur rechnerischen Ermittlung von . (3 BE)