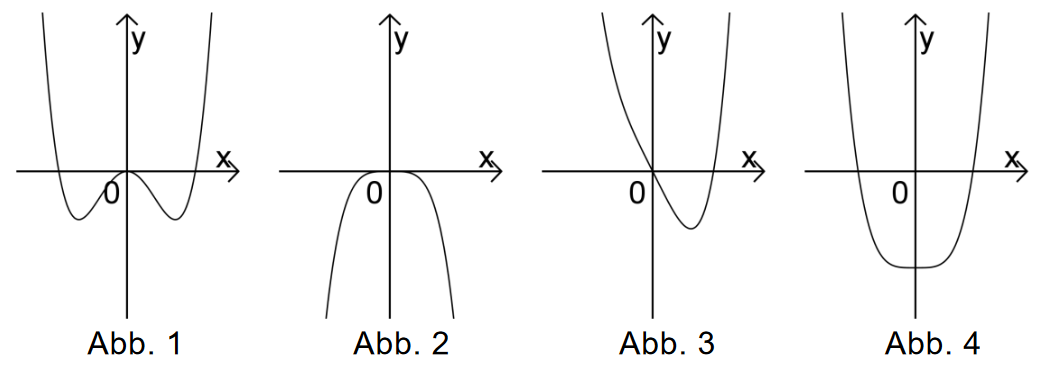Analysis, Teil B, Aufgabengruppe 2

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_n:x \mapsto x^4 - 2x^n$ mit $n \in \mathbb{N}$ sowie dir in $\mathbb{R}$ definierte Funktion $f_0:x \mapsto x^4-2$ .

Die Abbildungen 1 bis 4 zeigen die Graphen der Funktionen $f_0, f_1, f_2$ bzw $f_4$ . Ordnen Sie jeder dieser Funktionen den passenden Graphen zu und begründen Sie drei Ihrer Zuordnungen durch Aussagen zur Symmetrie, zu den Schnittpunkten mit den Koordinatenachsenoder dem Verhalten an den Grenzen des Definitionsbereichs des jeweiligen Graphen. (4 BE)
Betrachtet werden nun die Funktionen $f_n$ mit $n\gt4$ . Geben Sie in Abhängigkeit von $n$ das Verhalten dieser Funktionen für $x \rightarrow +\infty$ und für $x \rightarrow - \infty$ an. (3 BE)