Analysis, Teil B, Aufgabengruppe 1

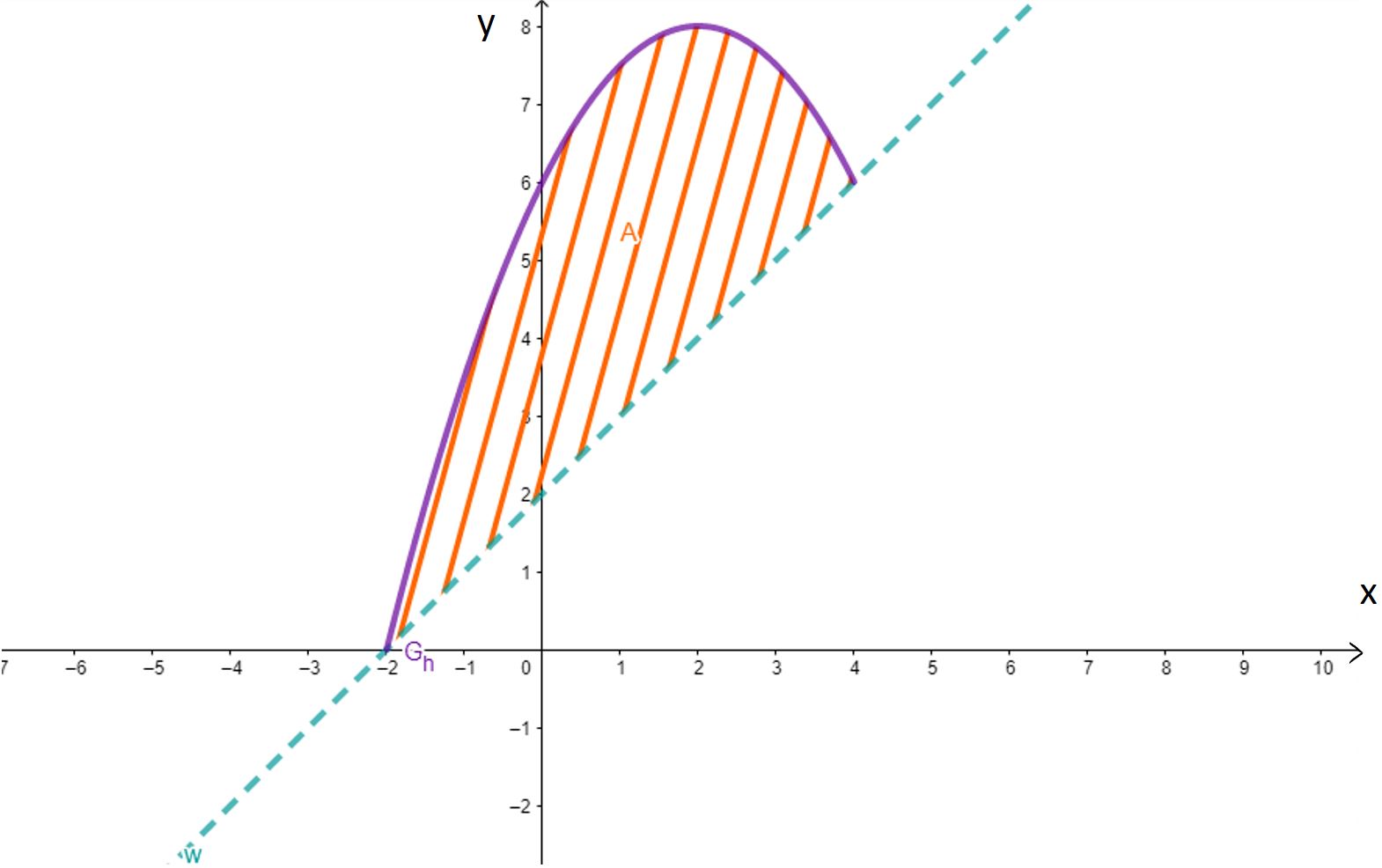
Durch die in Aufgabe 2 entstandene herzförmige Figur soll das abgebildete Blatt modellhaft beschrieben werden. Eine Längeneinheit im Koordinatensystem aus Aufgabe 1d soll dabei $1 cm$ in der Wirklichkeit entsprechen.

Berechnen Sie den Inhalt des von $G_{h}$ und der Winkelhalbierenden $w$ eingeschlossenen Flächenstücks. Bestimmen Sie unter Verwendung dieses Werts den Flächeninhalt des Blatts auf der Grundlage des Modells. (5BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integralrechnung
Bestimmung des Flächeninhalts
Bestimme den Flächeninhalt $A$ des Flächenstücks zwischen dem Graph $G_{h}$ und der Winkelhalbierenden $w$ . Hierzu brauchst du die Integralrechnung.
Du berechnest das Integral von $h (x)$ von $2$ bist $4$ und ziehst das Integral von $w (x)$ im gleichen Bereich ab. Da das Integral, aber eine Flächenbilanz angibt musst du beide Funktionen um $2$ nach oben verschieben. Dein Flächenstück befindet sich somit gänzlich über der $x$ -Achse. Rechnerisch musst du nur zu jeder Funktion $2$ addieren.
$h (x) + 2 = - \frac{1}{2} x^{2} + 2 x + 6$
$w (x) + 2 = x + 2$
Du musst die orange Fläche berechnen.
$ A = \int_{- 2}^{4} h (x) + 2 d x - \int_{- 2}^{4} w (x) + 2 d x$
Um weiter zu rechnen benutzt du den Hauptsatz der Differential- und Integralrechnung.
Forme zuerst um.
$A = \int_{- 2}^{4} h (x) + 2 d x - \int_{- 2}^{4} w (x) + 2 d x$
$= \int_{- 2}^{4} h (x) + 2 - (w (x) + 2) d x = \int_{- 2}^{4} h (x) - w (x) d x$
Jetzt kannst eine Stammfunktion finden und den HDI anwenden.
$A = \int_{- 2}^{4} h (x) - w (x) = \int_{- 2}^{4} - \frac{1}{2} x^{2} + x + 4 = [- \frac{1}{6} x^{3} + \frac{1}{2} x^{2} + 4 x] \begin{array}{c} 4 \\ - 2 \end{array} = (- \frac{1}{6} \cdot 4^{3} + \frac{1}{2} \cdot 4^{2} + 4 \cdot 4) - (- \frac{1}{6} \cdot (- 2)^{3} + \frac{1}{2} \cdot (- 2)^{2} + 4 \cdot (- 2)) = 18$
Das Flächenstück zwischen den Graphen $G_{h}$ und $G_{w}$ ist $18 c m^{2}$ .
Flächeninhalt des Blattes
Du hast in Aufgabe 2b) ein Modell eines Blattes erstellt. Darin kannst du deutlich sehen, dass das Blatt den doppelten Flächeninhalt hat bezogen auf A. $B$ ist hierbei der Flächeninhalt des Blattes.
$B = 2 \cdot A = 2 \cdot 18 = 36$
Der Flächeninhalt des Blattes beträgt $36 c m^{2}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
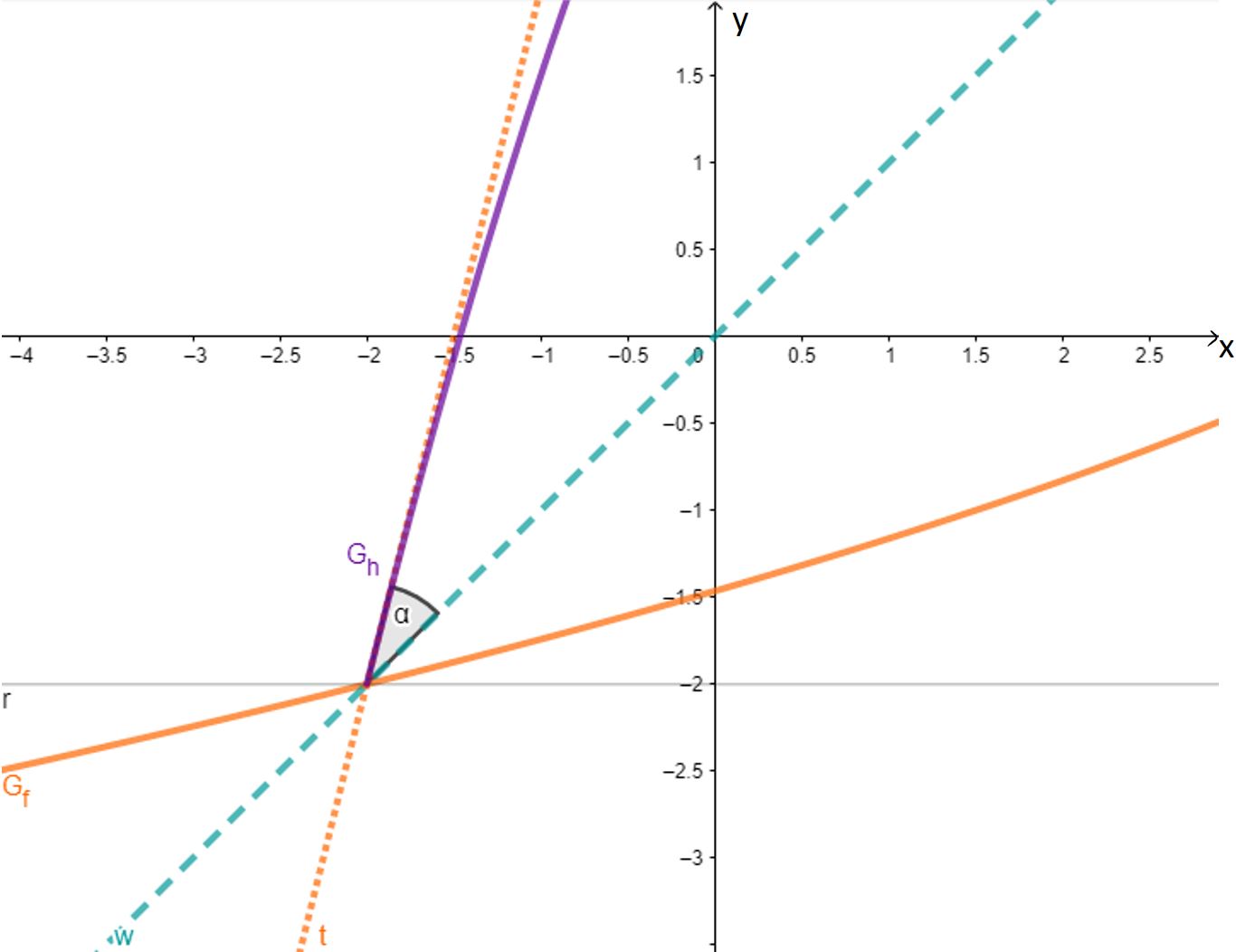
Ermitteln Sie die Gleichung der Tangente an $G_{h}$ im Punkt $(- 2 | (- 2))$ . Berechnen Sie den Wert, den das Modell für die Größe des Winkels liefert, den die Blattränder an der Blattspitze einschließen. (6BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangentengleichung
Tangente von $G_{h}$
Bestimme die Gleichung der Tangente an $G_{h}$ im Punkt $(- 2 | h (- 2))$ .
Berechne zuerst den Wert deiner $y$ -Koordinate.
$h (- 2) = - \frac{1}{2} \cdot 4 - 4 + 4 = - 2$
Deine Tangente soll also im Punkt $(- 2 | - 2)$ sein.
Bestimme die Ableitung $h^{'}$ von $h$ .
$h^{'} (x) = - x + 2$
Deine Tangente besitzt die allgemeine Form einer Geraden.
$y = m x + t$
Damit du die Steigung $m$ berechnen kannst, musst du den $x$ -Wert deines Punktes in $h^{'} (x)$ einsetzen.
$h (- 2) = - (- 2) + 2 = 4$
Berechne $t$ , indem du deinen Punkt in die Tangentengleichung einsetzt und nach $t$ auflöst.
$- 2 = 4 \cdot (- 2) + t$
$- 2 = - 8 + t | + 8$
$t = 6$
Stelle nun die Gleichung der Tangente $t$ auf.
$t (x) = 4 \cdot x + 6$
Bestimmung des Winkels, den die Blattspitze einschließt
Bestimme den Winkel zwischen den Funktionen $h (x)$ und $w (x)$ .
Du kannst erkennen, dass der Winkel, der von der Blattspitze eingeschlossen wird, die doppelte Größe von $α$ hat.
Berechne den Winkel $β$ zwischen der Tangente $t$ und der Waagrechten $r$ . Dazu musst du Tangens von $β$ gleich der Steigung von $t$ , also gleich $4$ setzen.
$\tan (β) = 4 \Leftrightarrow β = {75,96}^{\circ}$
Der Winkel zwischen der Tangente und der Waagrechten beträgt ${75,96}^{\circ}$ .
Du weißt schon, dass die Winkelhalbierende eines Quadranten des Koordinatensystems in einem $45^{\circ}$ -Winkel auf jeder Waagrechten steht also auch auf $r$ .
Wie du in der Zeichung sehen kannst, ist der Winkel $α$ die Differenz zwischen dem Winkel $β$ und dem Winkel zwischen $w$ und $r$ .
$α = β - 45^{\circ} = {75,96}^{\circ} - 45^{\circ} = {30,96}^{\circ}$
Der Winkel $α$ hat ${30,96}^{\circ}$ .
Der Winkel, den die Blattspitzen einschließen, ist:
$2 \cdot α = 2 \cdot {30,96}^{\circ} = {61,92}^{\circ}$ .
Der Winkel, der von der Blattspitze eingeschlossen wird, beträgt ${61,92}^{\circ}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Verlauf des oberen Blattrands wird in der Nähe der Blattspitze durch das bisher verwendete Modell nicht genau genug darstellt. Daher soll der obere Blattrand im Modell für $- 2 \leq x \leq 0$ nicht mehr durch $G_{h}$ , sondern durch den Graphen $G_{k}$ einer in $ℝ$ definierten ganzrationalen Funktion $k$ dritten Grades beschrieben werden. Für die Funktion k werden die folgenden Bedingungen gewählt ( $k^{'}$ und $h^{'}$ sind die Ableitungsfunktionen von $k$ bzw. $h$ ):
$\begin{array}{crcrcrcr} I & k (0) & = & h (0) \\ II & k^{'} (0) & = & h^{'} (0) \\ III & k (- 2) & = & h (- 2) \\ IV & k^{'} (- 2) & = & 1,5 \end{array}$
Begründen Sie im Sachzusammenhang, dass die Wahl der Bedingungen I,II und III sinnvoll ist. Machen Sie plausibel, dass die Bedingung IV dazu führt, dass die Form des Blatts in der Nähe der Blattspitze im Vergleich zum ursprünglichen Modell genauer dargestellt wird. (3BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Bedingungen I,II und III
Mit Bedingung I und II stellst du sicher, dass die Funktionen $h$ und $k$ nahtlos ineinander übergehen. Genauer sagt dir die Bedingung I, dass $h$ und $k$ für $x$ gleich $0$ den gleichen Funktionswert haben, und die Bedingung II, dass sie an diesem Punkt auch die gleiche Steigung haben.
Die III. Bedingung sagt dir, dass die beiden Funktionen wieder am gleichen Punkt zusammenlaufen. Also am Punkt $(- 2 | - 2)$ das Ende der Blattspitze bleibt.
Bedingung IV
In der IV. Bedingung musst du erkennen, dass hier die Funktion $k$ von der ursprünglichen Funktion $h$ abweicht. Führ dir den Unterschied vor Augen, indem du die Werte berechnest.
$k^{'} (- 2) = 1,5$
$h^{'} (- 2) = - (- 2) + 2 = 4$
Du siehst der ursprüngliche Rand verläuft steiler, da er eine größere Steigung hat. Die Bedingung IV verursacht eine Abflachung an der Blattspitze, das ist die Kurve nach innen, die du auf dem Bild erkennen kannst.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇