Finde eine Stammfunktion für die -Funktion mithilfe des Formansatzes.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Damit eine Stammfunktion von ist, muss gelten .
Bilde die Ableitung von , beachte dabei die Produkt- und Kettenregel.
Der Koeffizientenvergleich von und liefert folgendes Gleichungssystem:
Setze in Gleichung ein
Mit und ergibt sich die allgemeine Stammfunktion zu:
Hast du eine Frage oder Feedback?
Der Term vor der -Funktion ist linear. Verwende deshalb einen Ansatz mit einer allgemeinen linearen Funktion . Der Formansatz für die Stammfunktion lautet dann . Bilde die Ableitung von und führe einen Koeffizientenvergleich mit durch.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Damit eine Stammfunktion von ist, muss gelten .
Bilde die Ableitung von , beachte dabei die Produkt- und Kettenregel.
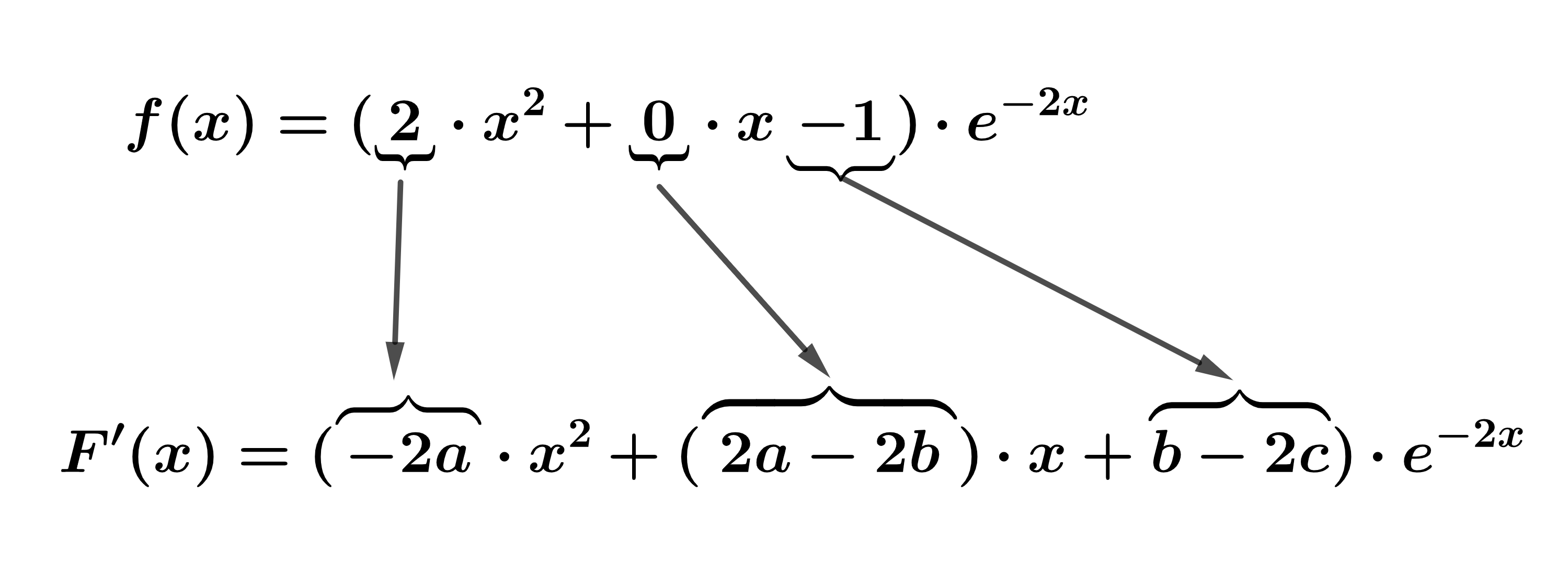
Beachte bei der Funktion den Einschub des Terms .
Der Koeffizientenvergleich von und liefert folgendes Gleichungssystem:
Setze in ein
Setze in ein
Mit , und ergibt sich die allgemeine Stammfunktion zu:
Hast du eine Frage oder Feedback?
Der Term vor der -Funktion ist quadratisch. Verwende deshalb einen Ansatz mit einer allgemeinen quadratischen Funktion . Der Formansatz für die Stammfunktion lautet dann . Bilde die Ableitung von und führe einen Koeffizientenvergleich mit durch.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

