Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Spiegelung einer Ebene an einer Ebene

Der Artikel beschreibt die Spiegelung einer Ebene EE an einer Ebene HH.

Es werden zwei verschiedene Berechnungsmethoden beschrieben.

Berechnungsmethode 1

Es werden zwei Fälle untersucht:

1. Fall: Die beiden Ebenen sind (echt) parallel zueinander.

2. Fall: Die beiden Ebenen schneiden sich in einer Geraden gSg_S. Die Berechnung der gespiegelten Ebene EE' erfolgt mit einer Lotgeraden lLotl_{Lot}.

Berechnungsmethode 2

Bestimme von der Ebene EE drei nicht kollineare Punkte P,QP, Q und RR. Berechne nacheinander die drei an der Ebene EE gespiegelten Punkte P′,Q′P{}', Q{}' und R′ R{ }'. Erstelle dann mit diesen drei Spiegelpunkten eine Parameterform der Spiegelebene E′E'.

Berechnungsmethode 1 Fall 1:

Vorgehensweise

Abstände paralleler Ebenen

Gegeben sind zwei (echt) parallele Ebenen in Koordinatenform:

E:  a1⋅x1+b1⋅x2+c1⋅x3=d1E:\; a_1\cdot x_1+b_1\cdot x_2+c_1\cdot x_3=d_1 und H:  a1⋅x1+b1⋅x2+c1⋅x3=d2H:\; a_1\cdot x_1+b_1\cdot x_2+c_1\cdot x_3=d_2.

Die Ebene EE wird an der Ebene HH gespiegelt  ⇒  E′:  a1⋅x1+b1⋅x2+c1⋅x3=d3\;\Rightarrow\;E':\;a_1\cdot x_1+b_1\cdot x_2+c_1\cdot x_3=d_3

Wie wird d3d_3 berechnet?

Setzt man den Koordinatenursprung in die Hessesche Normalenform der Ebene ein, so erhält man den Abstand der Ebene vom Ursprung.

EHNF:a1x1+b1x2+c1x3−d1∣n⃗E∣=0E_{HNF}: \dfrac{a_1x_1+b_1x_2+c_1x_3-d_1}{|\vec n_E|}=0

d(O,E)=∣a1⋅0+b1⋅0+c1⋅0−d1∣n⃗E∣∣=d1∣n⃗E∣d(O,E)=\left|\dfrac{a_1\cdot 0+b_1\cdot 0+c_1\cdot 0-d_1}{|\vec n_E|}\right|=\dfrac{d_1}{|\vec n_E|}

Entsprechend für die Ebene HH:

d(O,H)=∣a1⋅0+b1⋅0+c1⋅0−d2∣n⃗H∣∣=d2∣n⃗H∣d(O,H)=\left|\dfrac{a_1\cdot 0+b_1\cdot 0+c_1\cdot 0-d_2}{|\vec n_H|}\right|=\dfrac{d_2}{|\vec n_H|}

Für den Abstand der Spiegelebene E′E' vom Koordinatenursprung gilt:

d(O,E′)=d(O,H)+d(E,H)=d(O,H)+(d(OH)−d(O,E))=2⋅d(O,H)−d(O,E)d(O,E')=d(O,H)+d(E,H)=d(O,H)+(d(OH)-d(O,E))=2\cdot d(O,H)-d(O,E)

Da ∣n⃗E∣=∣n⃗H∣=∣n⃗E′∣|\vec n_E|=|\vec n_H|=|\vec n_E'| gilt: d(O,E′)=d3∣n⃗E∣=2⋅d2∣n⃗E∣−d1∣n⃗E∣d(O,E')=\dfrac{d_3}{|\vec n_E|}=2\cdot \dfrac{d_2}{|\vec n_E|}-\dfrac{d_1}{|\vec n_E|}

Für d3d_3 der Spiegelebene E′E' ergibt sich somit die Gleichung:

Beispiel zu Fall 1

Gegeben sind die beiden (echt) parallelen Ebenen

E:  5⋅x1−x2+2⋅x3=−3E:\; 5\cdot x_1- x_2+2\cdot x_3=-3 und H:  5⋅x1−x2+2⋅x3=−30H:\; 5\cdot x_1- x_2+2\cdot x_3=-30 .

Die Ebene EE wird an der Ebene HH gespiegelt.

d3=2⋅d2−d1d_3=2\cdot d_2-d_1

Setze d1=−3d_1=-3 und d2=−30d_2=-30 ein:

d3=2⋅(−30)−(−3)=−60+3=−57d_3=2\cdot(-30)-(-3)=-60+3=-57

Antwort: Die Gleichung der Spiegelebene E′ E' lautet: 5⋅x1−x2+2⋅x3=−575\cdot x_1- x_2+2\cdot x_3=-57

Grafische Darstellung der 3 parallelen Ebenen für das Beispiel zu Fall 1

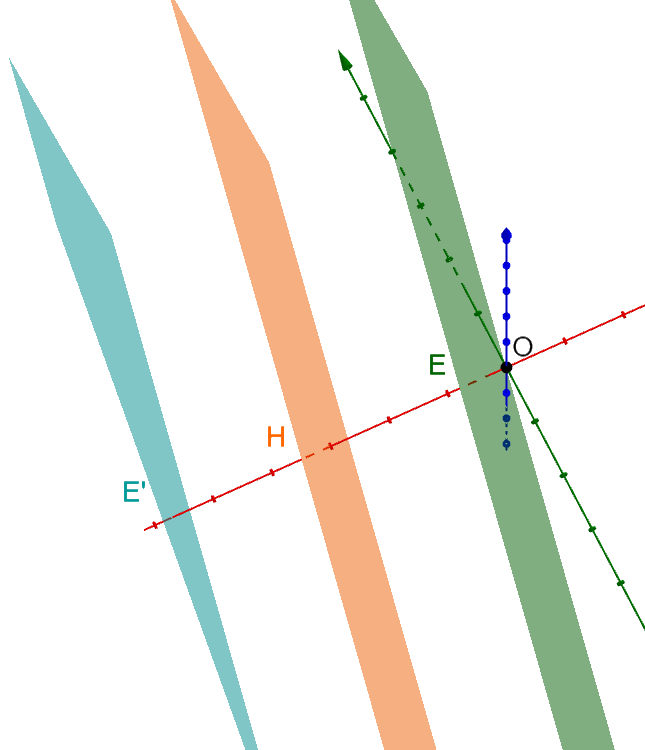
Grafische Darstellung der 3 parallelen Ebenen

Berechnungsmethode 1 Fall 2:

Gegeben sind zwei Ebenen in Koordinatenform E:  a1⋅x1+b1⋅x2+c1⋅x3=d1E:\; a_1\cdot x_1+b_1\cdot x_2+c_1\cdot x_3=d_1 und

H:  a2⋅x1+b2⋅x2+c2⋅x3=d2H:\; a_2\cdot x_1+b_2\cdot x_2+c_2\cdot x_3=d_2. Die beiden Ebenen schneiden sich in der Schnittgeraden gSg_S. Die Ebene EE wird an der Ebene HH gespiegelt.

Vorgehensweise

Berechnung der gespiegelten Ebene EE' mit einer Lotgeraden lLotl_{Lot}

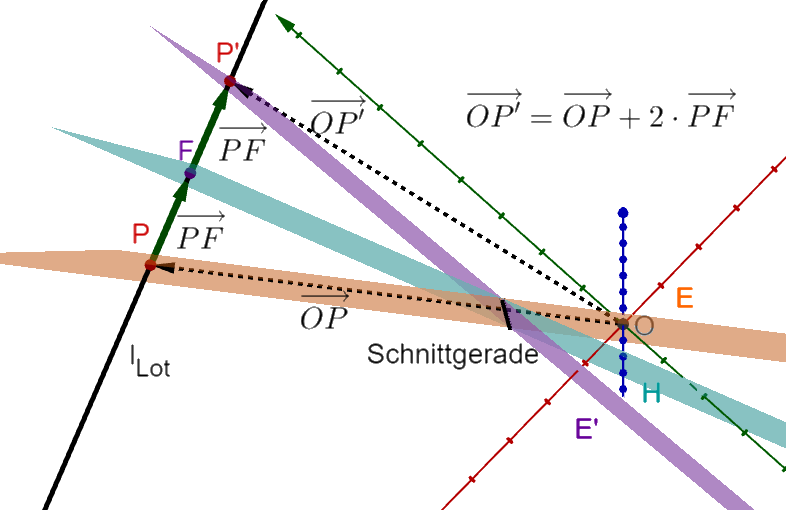
Spiegelung einer Ebene an einer Ebene, 2 sich schneidende Ebenen

1. Die Schnittgerade gSg_S ist gegeben: gS:  x⃗=OA→+t⋅u⃗g_S:\;\vec x=\overrightarrow{OA}+t\cdot \vec u oder muss berechnet werden.

2. Finde einen Punkt PP auf der Ebene EE. Der Punkt PP darf nicht auf der Schnittgeraden gSg_S liegen.

3. Erstelle eine Lotgerade lLotl_{Lot} mit dem gefundenen Punkt PP als Aufpunkt und dem Normalenvektor n⃗H=(a2b2c2)\vec n_H=\begin{pmatrix}a_2\\b_2\\c_2\end{pmatrix} der Ebene HH: lLot:x⃗=OP→+r⋅n⃗Hl_{Lot}:\vec x=\overrightarrow{OP}+r \cdot \vec n_H

4. Schneide die Lotgerade lLotl_{Lot} mit der Ebene HH. Du erhältst den Fußpunkt FF.

5. Berechne den Vektor PF→\overrightarrow{PF}

6. Zur Berechnung des Spiegelpunktes P′P' setze OP→\overrightarrow{OP} und PF→\overrightarrow{PF} in die Vektorgleichung OP′→=OP→+2⋅PF→\overrightarrow{OP'}=\overrightarrow{OP}+2\cdot\overrightarrow{PF} ein.

7. Der berechnete Punkt P′P' ist ein Punkt der Spiegelebene E′E'. Erstelle eine Parameterform für die Spiegelebene E′E' mit der Schnittgeraden gS g_S und einem weiteren Richtungsvektor v⃗=AP′→\vec v=\overrightarrow{AP'} (AA ist der Aufpunkt der Schnittgeraden)   ⇒   \;\Rightarrow\; E′:  x⃗=OA→+r⋅u⃗+s⋅v⃗E':\; \vec x=\overrightarrow{OA}+r\cdot \vec u+s\cdot \vec v.

Beispiel zu Fall 2

Gegeben sind die beiden Ebenen E:  7⋅x1−5⋅x2−3⋅x3=0E:\; 7\cdot x_1-5\cdot x_2-3\cdot x_3=0 und H:  3⋅x1−x2−x3=2H:\; 3\cdot x_1- x_2- x_3=2. Die Gleichung der Schnittgeraden lautet: gS:  x⃗=(307)+r⋅(−11−4)g_S:\;\vec x=\begin{pmatrix}3\\0\\7\end{pmatrix}+r\cdot\begin{pmatrix}-1\\1\\-4\end{pmatrix}

Die Ebene EE wird an der Ebene HH gespiegelt.

1. Die Schnittgerade gSg_S ist gegeben: gS:  x⃗=OA→+r⋅u⃗=(307)+r⋅(−11−4)g_S:\;\vec x=\overrightarrow{OA}+r\cdot \vec u =\begin{pmatrix}3\\0\\7\end{pmatrix}+r\cdot\begin{pmatrix}-1\\1\\-4\end{pmatrix}.

2. Finde einen Punkt PP auf der Ebene EE. Der Punkt PP darf nicht auf der Schnittgeraden gSg_S liegen.

E:  7⋅x1−5⋅x2−3⋅x3=0E:\; 7\cdot x_1-5\cdot x_2-3\cdot x_3=0

Wähle z.B. P(5∣7∣0)P(5|7|0). P∈E P\in E ?  ⇒  7⋅5−5⋅7−3⋅0=0  ✓\;\Rightarrow\;7\cdot5-5\cdot7-3\cdot0=0\;\checkmark

Liegt PP auf gSg_S? Setze PP in die Geradengleichung ein:

(570)=(307)+r⋅(−11−4)  ⇒  (27−7)=r⋅(−11−4)\begin{pmatrix}5\\7\\0\end{pmatrix}=\begin{pmatrix}3\\0\\7\end{pmatrix}+r\cdot\begin{pmatrix}-1\\1\\-4\end{pmatrix}\;\Rightarrow\;\begin{pmatrix}2\\7\\-7\end{pmatrix}=r\cdot\begin{pmatrix}-1\\1\\-4\end{pmatrix}

Aus der ersten Zeile folgt r=−2 r=-2 und aus der zweiten Zeile folgt r=7r=7. Somit liegt PP nicht auf gS.g_S.

3. Erstelle eine Lotgerade lLotl_{Lot} mit dem gefundenen Punkt P(5∣7∣0)P(5|7|0) als Aufpunkt und dem Normalenvektor n⃗H=(3−1−1)\vec n_H=\begin{pmatrix}3\\-1\\-1\end{pmatrix} der Ebene HH: lLot:x⃗=(570)+r⋅(3−1−1)l_{Lot}:\vec x=\begin{pmatrix}5\\7\\0\end{pmatrix}+r\cdot\begin{pmatrix}3\\-1\\-1\end{pmatrix}

4. Schneide die Lotgerade lLotl_{Lot} mit der Ebene HH.

3⋅x1−x2−x3\displaystyle 3\cdot x_1- x_2- x_3==2\displaystyle 2
↓

Setze die Lotgerade lLot:x⃗=(570)+r⋅(3−1−1)l_{Lot}:\vec x=\begin{pmatrix}5\\7\\0\end{pmatrix}+r\cdot\begin{pmatrix}3\\-1\\-1\end{pmatrix}in HH ein.

3⋅(5+3r)−(7−r)−(0−r)\displaystyle 3\cdot(5+3r)-(7-r)-(0-r)==2\displaystyle 2
↓

Löse die Klammern auf.

15+9r−7+r+r\displaystyle 15+9r-7+r+r==2\displaystyle 2
↓

Fasse zusammen und löse nach rr auf.

8+11r\displaystyle 8+11r==2\displaystyle 2−8\displaystyle -8
11r\displaystyle 11r==−6\displaystyle -6:30\displaystyle :30
r\displaystyle r==−611\displaystyle -\dfrac{6}{11}

Setze r=−611r=-\dfrac{6}{11} in die Lotgerade lLotl_{Lot} ein, um den Punkt FF zu berechnen.

x⃗F=(570)+(−611)⋅(3−1−1)=(5−18117+6110+611)=(37118311611)  ⇒  \vec x_F= \begin{pmatrix}5\\7\\0\end{pmatrix}+(-\dfrac{6}{11}) \cdot \begin{pmatrix}3\\-1\\-1\end{pmatrix} =\begin{pmatrix}5-\dfrac{18}{11}\\[2ex] 7+\dfrac{6}{11}\\[2ex]0+\dfrac{6}{11}\end{pmatrix}=\begin{pmatrix}\dfrac{37}{11}\\[2ex] \dfrac{83}{11}\\[2ex]\dfrac{6}{11}\end{pmatrix}\;\Rightarrow\;F(3711∣8311∣611)F\left(\dfrac{37}{11}\Big\vert\dfrac{83}{11}\Big\vert\dfrac{6}{11}\right)

5. Berechne den Vektor PF→\overrightarrow{PF}

PF→=OF→−OP→=(37118311611)−(570)=(3711−58311−7611−0)=(−1811611611)\overrightarrow{PF}=\overrightarrow{OF}-\overrightarrow{OP}=\begin{pmatrix}\dfrac{37}{11}\\[2ex] \dfrac{83}{11}\\[2ex]\dfrac{6}{11}\end{pmatrix}-\begin{pmatrix}5\\7\\0\end{pmatrix}=\begin{pmatrix}\dfrac{37}{11}-5\\[2ex] \dfrac{83}{11}-7\\[2ex]\dfrac{6}{11}-0\end{pmatrix}=\begin{pmatrix}-\dfrac{18}{11}\\[2ex] \dfrac{6}{11}\\[2ex]\dfrac{6}{11}\end{pmatrix}

6. Setze OP→\overrightarrow{OP} und PF→\overrightarrow{PF} in die Vektorgleichung OP′→=OP→+2⋅PF→\overrightarrow{OP'}=\overrightarrow{OP}+2\cdot\overrightarrow{PF} ein:

OP′→=(570)+2⋅(−1811611611)=(5−36117+12110+1211)=(191189111211)\overrightarrow{OP'}=\begin{pmatrix}5\\7\\0\end{pmatrix}+2\cdot \begin{pmatrix}-\dfrac{18}{11}\\[2ex] \dfrac{6}{11}\\[2ex]\dfrac{6}{11}\end{pmatrix}=\begin{pmatrix}5-\dfrac{36}{11}\\[2ex]7+\dfrac{12}{11}\\[2ex]0+\dfrac{12}{11}\end{pmatrix}=\begin{pmatrix}\dfrac{19}{11}\\[2ex]\dfrac{89}{11}\\[2ex]\dfrac{12}{11}\end{pmatrix}

Der Spiegelpunkt hat die Koordinaten P′(1911∣8911∣1211)P'\left(\dfrac{19}{11}\Big\vert\dfrac{89}{11}\Big\vert\dfrac{12}{11}\right).

7. Der berechnete Punkt P′P' ist ein Punkt der Spiegelebene E′E'. Erstelle eine Parameterform für die Spiegelebene E′E' mit der Schnittgeraden gS g_S und einem weiteren Richtungsvektor v⃗=AP′→\vec v=\overrightarrow{AP'} (AA ist der Aufpunkt der Schnittgeraden)   ⇒   \;\Rightarrow\; E′:  x⃗=OA→+r⋅u⃗+s⋅v⃗E':\; \vec x=\overrightarrow{OA}+r\cdot \vec u+s\cdot \vec v.

Berechne den zweiten Richtungsvektor:

v⃗=AP′→=OP′→−OA→=(191189111211)−(307)=(1911−38911−01211−7)=(−14118911−6511)=111⋅(−1489−65)\vec v=\overrightarrow{AP'}=\overrightarrow{OP'}-\overrightarrow{OA}=\begin{pmatrix}\dfrac{19}{11}\\[2ex]\dfrac{89}{11}\\[2ex]\dfrac{12}{11}\end{pmatrix}-\begin{pmatrix}3\\0\\7\end{pmatrix}=\begin{pmatrix}\dfrac{19}{11}-3\\[2ex]\dfrac{89}{11}-0\\[2ex]\dfrac{12}{11}-7\end{pmatrix}=\begin{pmatrix}-\dfrac{14}{11}\\[2ex]\dfrac{89}{11}\\[2ex]-\dfrac{65}{11}\end{pmatrix}=\dfrac{1}{11}\cdot\begin{pmatrix}-14\\89\\-65\end{pmatrix}

Die Spiegelebene E′E' kann dann als Parametergleichung geschrieben werden:

E′:  x⃗=(307)+r⋅(−11−4)+s⋅(−1489−65)E':\;\vec x=\begin{pmatrix}3\\0\\7\end{pmatrix}+r\cdot\begin{pmatrix}-1\\1\\-4\end{pmatrix}+s\cdot \begin{pmatrix}-14\\89\\-65\end{pmatrix} oder umgewandelt in eine Koordinatenform:

E′:  291x1−9x2−75x3=348E':\;291x_1-9x_2-75x_3=348

Anmerkung: Die obige Abbildung zeigt das berechnete Beispiel im 2. Fall.


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?