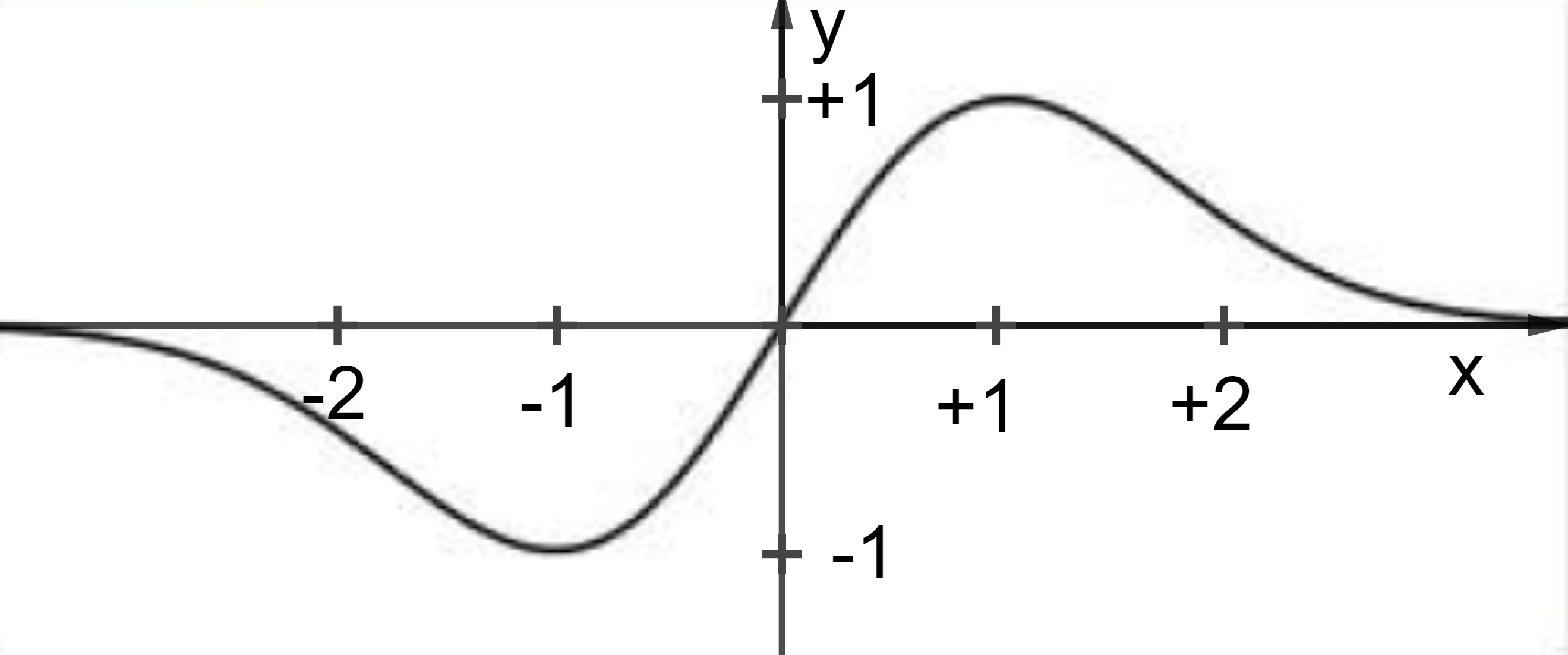
Gegeben ist die in definierte Funktion mit . Die Abbildung zeigt den Graphen von ohne das zugrunde liegende Koordinatensystem.
Zeigen Sie anhand des Funktionsterms von , dass der Graph von symmetrisch bezüglich des Koordinatenursprungs ist. Begründen Sie, dass genau eine Nullstelle hat, und geben Sie den Grenzwert von für an. (4P)
Bestimmen Sie einen Term der ersten Ableitungsfunktion von . (2P)
(zur Kontrolle: )
Untersuchen Sie rechnerisch das Monotonieverhalten von . Ergänzen Sie in der Abbildung die Koordinatenachsen und skalieren Sie diese passend. (5P)
Ist die erste Ableitungsfunktion einer in definierten Funktion , so gilt bekanntlich . Berechnen Sie damit den Wert des Terms . (3P)
Interpretieren Sie den folgenden Sachverhalt geometrisch:
Für jede Stammfunktion von und für jede reelle Zahl gilt
. (3P)