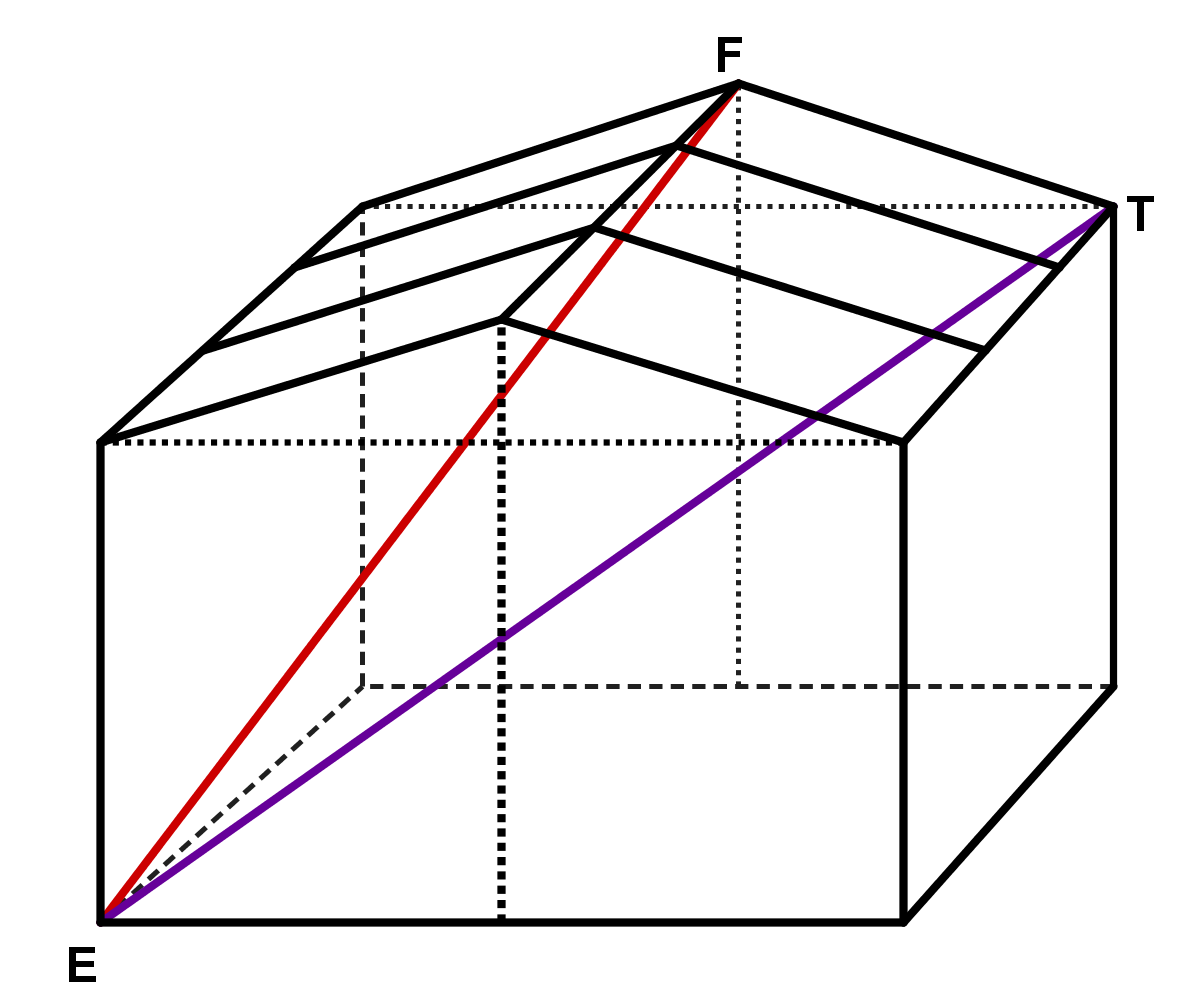
Betrachte folgendes Holzhäuschen (Maße in ):

Wie lang ist der längste Faden, den eine Spinne geradlinig im Holzhäuschen spannen könnte?
Teilaufgabe 1
Vorüberlegung und Lösungsplan:
Betrachtest du die Zeichnung, dann siehst du:
Der längste Faden ist entweder so lang wie
die Strecke (denn diese geht von der unteren Ecke des Raumes in die entgegengesetzt gelegene obere Ecke)
oder so lang wie
die Strecke (denn um von zu zu kommen, muss die Spinne zwar weniger weit nach rechts, als wenn sie zu webt, aber dafür etwas weiter nach oben).
Berechnung der Länge der Strecke
Die Strecke ist Seite im Dreieck .
Dieses Dreieck hat bei einen rechten Winkel.
Also kannst du im Dreieck den Satz von Pythagoras anwenden.
Die Hypotenuse ist .

Die Streckenlänge ist in der Aufgabenstellung angegeben (denn die Strecke ist natürlich genauso lang wie .
kannst du daher einfach in die Gleichung einsetzen,
aber die Länge musst du noch gesondert berechnen.
Berechnung von :
Die Strecke ist Seite im Dreieck am Boden des Holzhäuschens.
Dieses Dreieck ist bei rechtwinklig. Also kannst du auch in ihm den Satz von Pythagoras anwenden.
Die Hypotenuse ist .
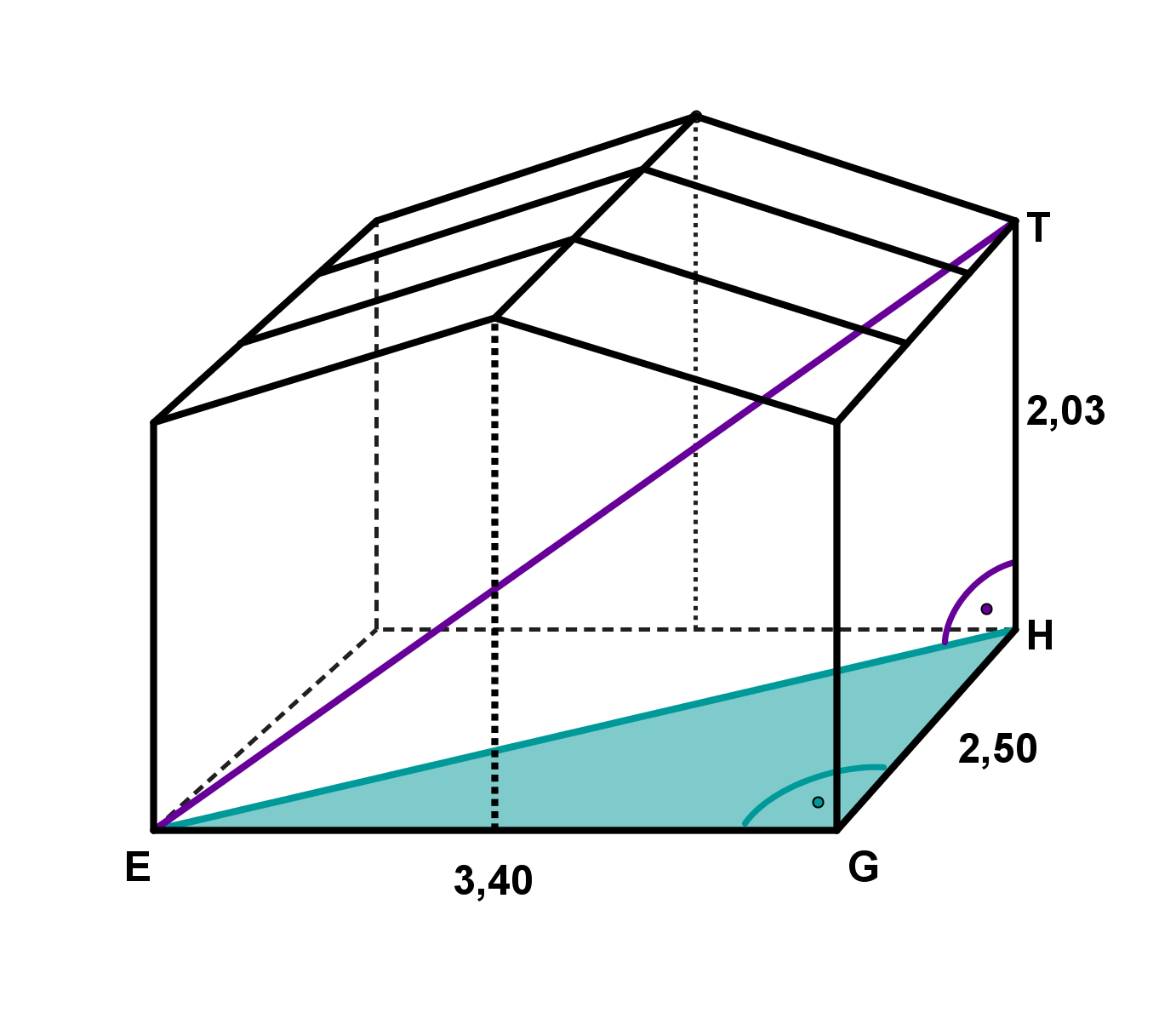
und sind in der Aufgabe gegeben; setze sie ein
und rechne aus.
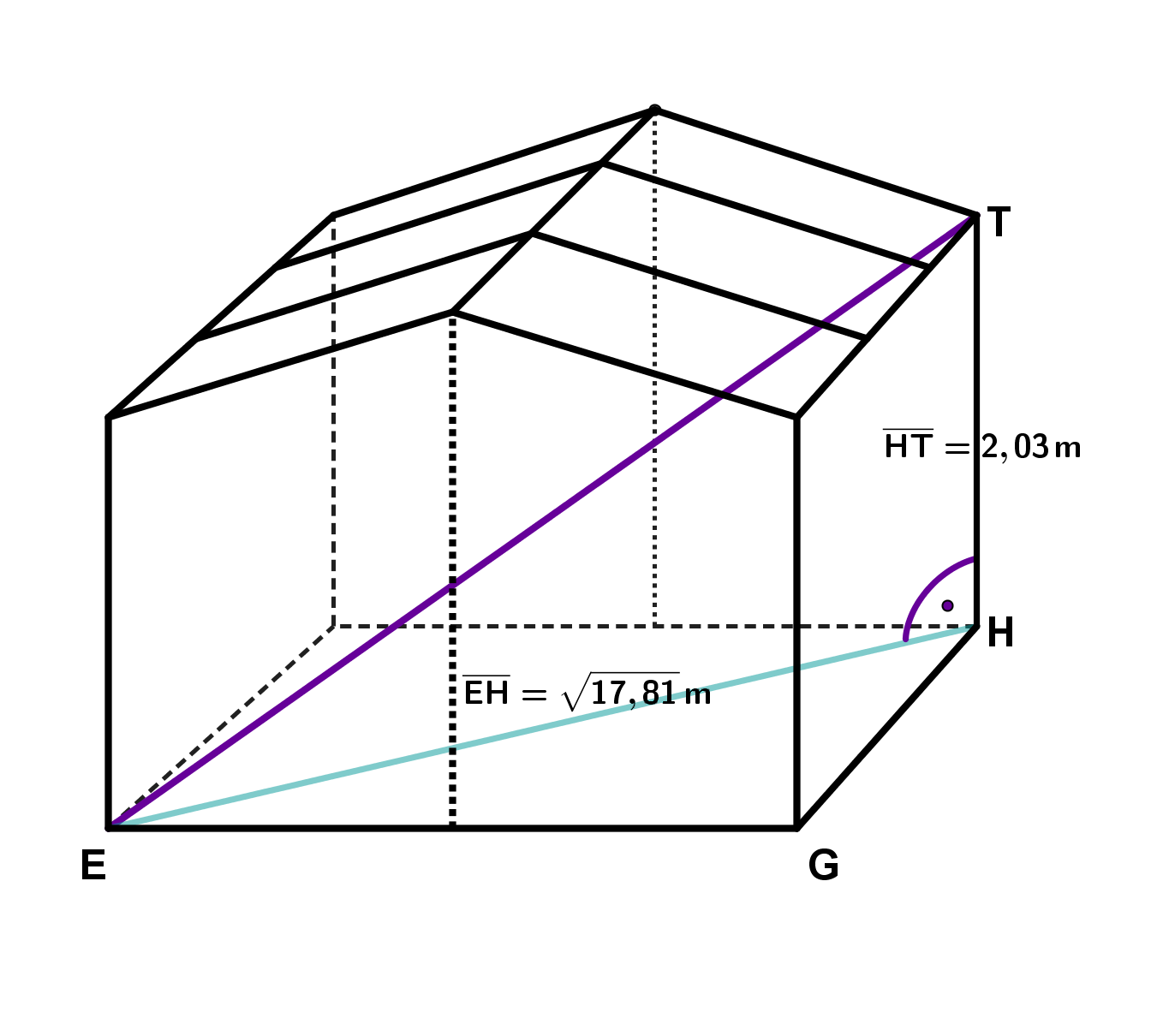
Um von zu zu kommen, kannst du nun die Wurzel anwenden.
Wenn du einen ungefähren Wert für wissen willst, kannst du diesen jetzt mit dem Taschenrechner ausrechnen:
(Du musst diesen Schritt aber auch nicht machen, da ohnehin mit weitergerechnet wird.)
Berechnung der Streckenlänge mithilfe des errechneten :
Du hast bislang erhalten:
und
.
Setze nun in die obere Gleichung ein.
Berechnung der Länge der Strecke
Die Strecke ist Seite im Dreieck .
Dieses Dreieck hat bei einen rechten Winkel.
Also kannst du im Dreieck den Satz des Pythagoras anwenden.
Die Hypotenuse ist .
Die Streckenlänge ist in der Aufgabenstellung angegeben (denn die Strecke ist natürlich genauso lang wie .
kannst du daher einfach in die Gleichung einsetzen,
aber die Länge musst du wieder gesondert berechnen.
Berechnung von :
Die Strecke ist Seite im Dreieck am Boden des Holzhäuschens.
Dieses Dreieck ist bei rechtwinklig. Also kannst du auch in ihm den Satz von Pythagoras anwenden.
Die Hypotenuse ist .
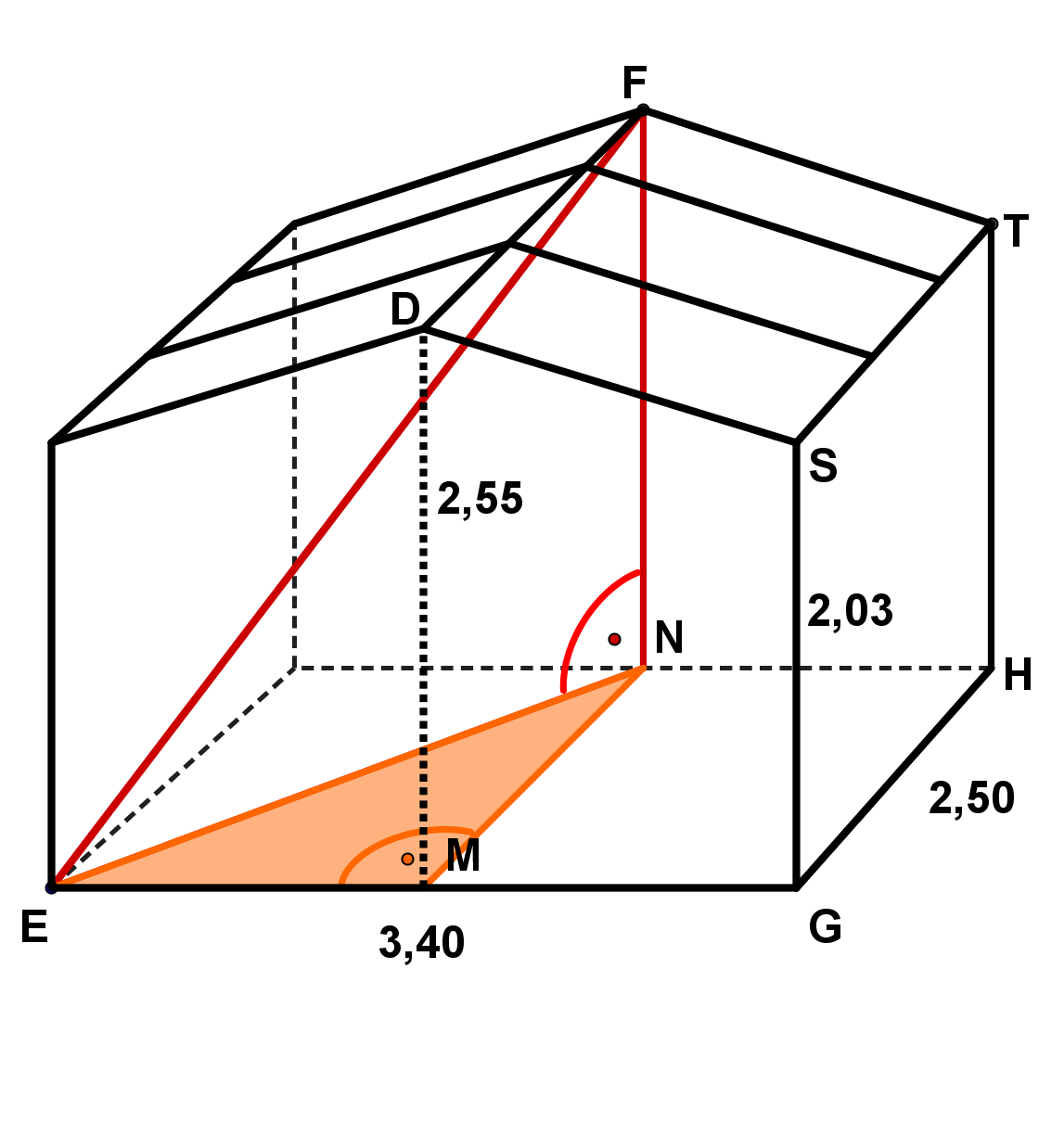
Die Streckenlänge ist angegeben und du kannst sie einsetzen (denn die Strecke ist natürlich genauso lang wie ).
ist halb so lang , und ist ebenfalls in der Aufgabenstellung angegeben.
↓ Um von zu zu kommen, kannst du nun die Wurzel anwenden.
↓ Wenn du einen ungefähren Wert für wissen willst, kannst du diesen jetzt mit dem Taschenrechner ausrechnen:
(Du musst diesen Schritt aber auch nicht machen, da ohnehin mit weitergerechnet wird.)
Berechnung der Streckenlänge mithilfe des errechneten :
Du hast bislang erhalten:
und
.
Setze nun in die obere Gleichung ein.
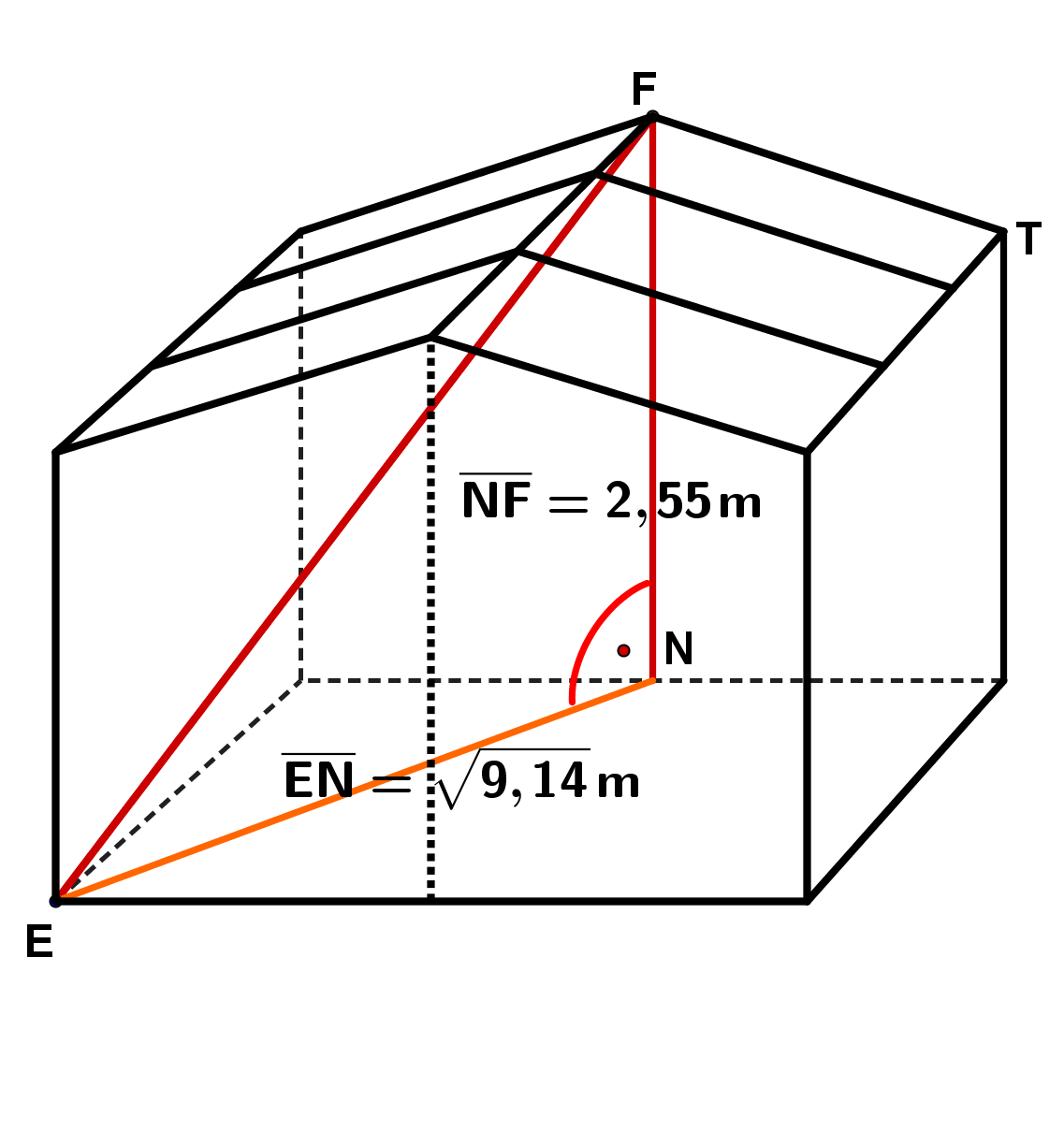
Ergebnis
Die Strecke mit einer Streckenlänge von ca. ist größer als die Strecke .
Damit ist die Strecke der längste Faden, den die Spinne geradlinig spannen kann.
Hast du eine Frage oder Feedback?
Plan zur Lösung der Aufgabe:
Berechne zuerst die Längen der beiden Strecken und ,
und prüfe dann, welche von beiden die längere ist.
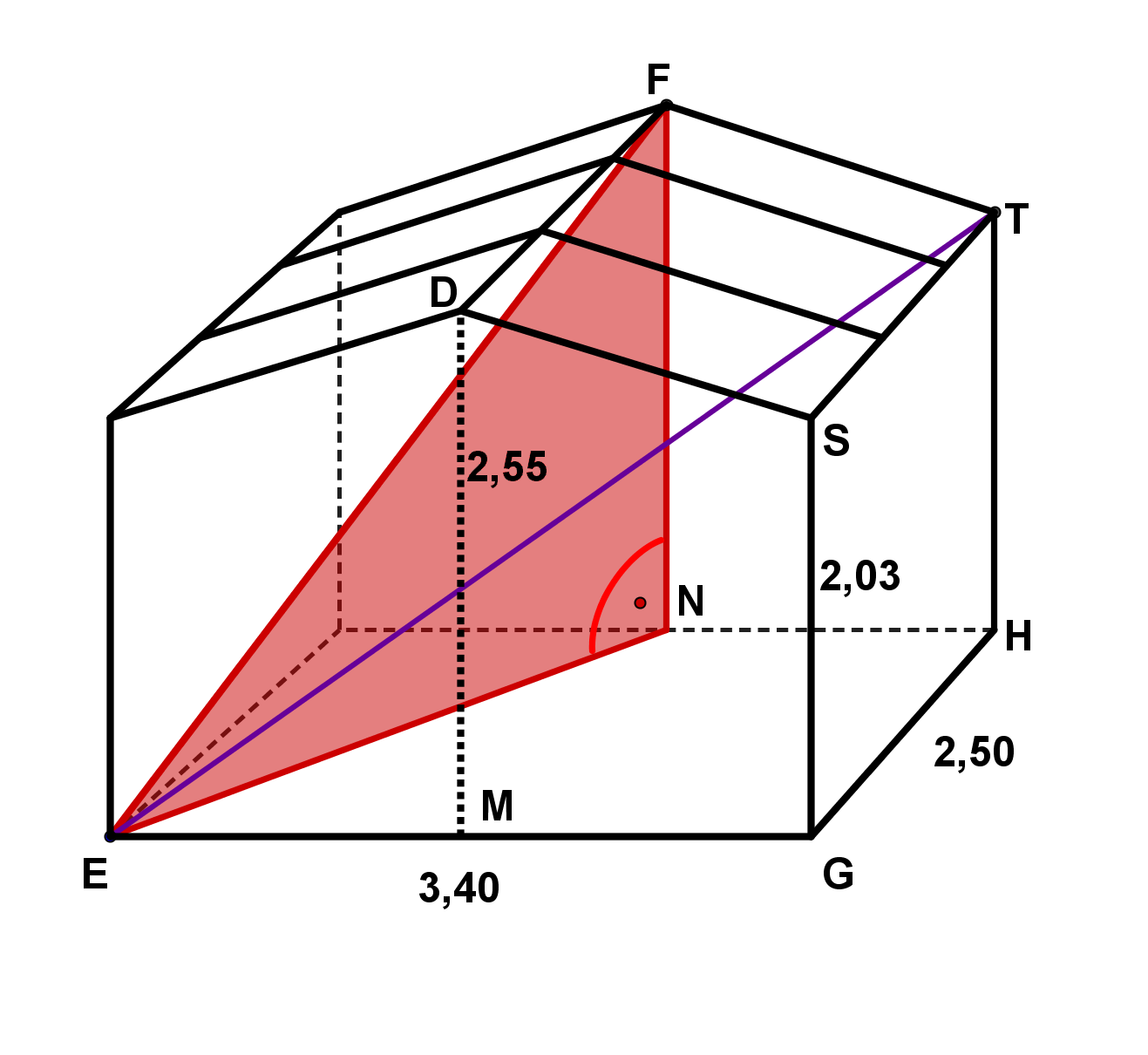
Wie viel Dachfläche hat das Holzhäuschen?
Teilaufgabe 2
Vorüberlegung und Lösungsplan:
Betrachtest du die Zeichnung, dann siehst du:
Die Dachfläche besteht aus zwei Rechtecken, die beide gleich groß sind.
Plan zur Lösung der Aufgabe:
Berechne die Fläche des Rechtecks und
multipliziere das Ergebnis anschließend mit 2.
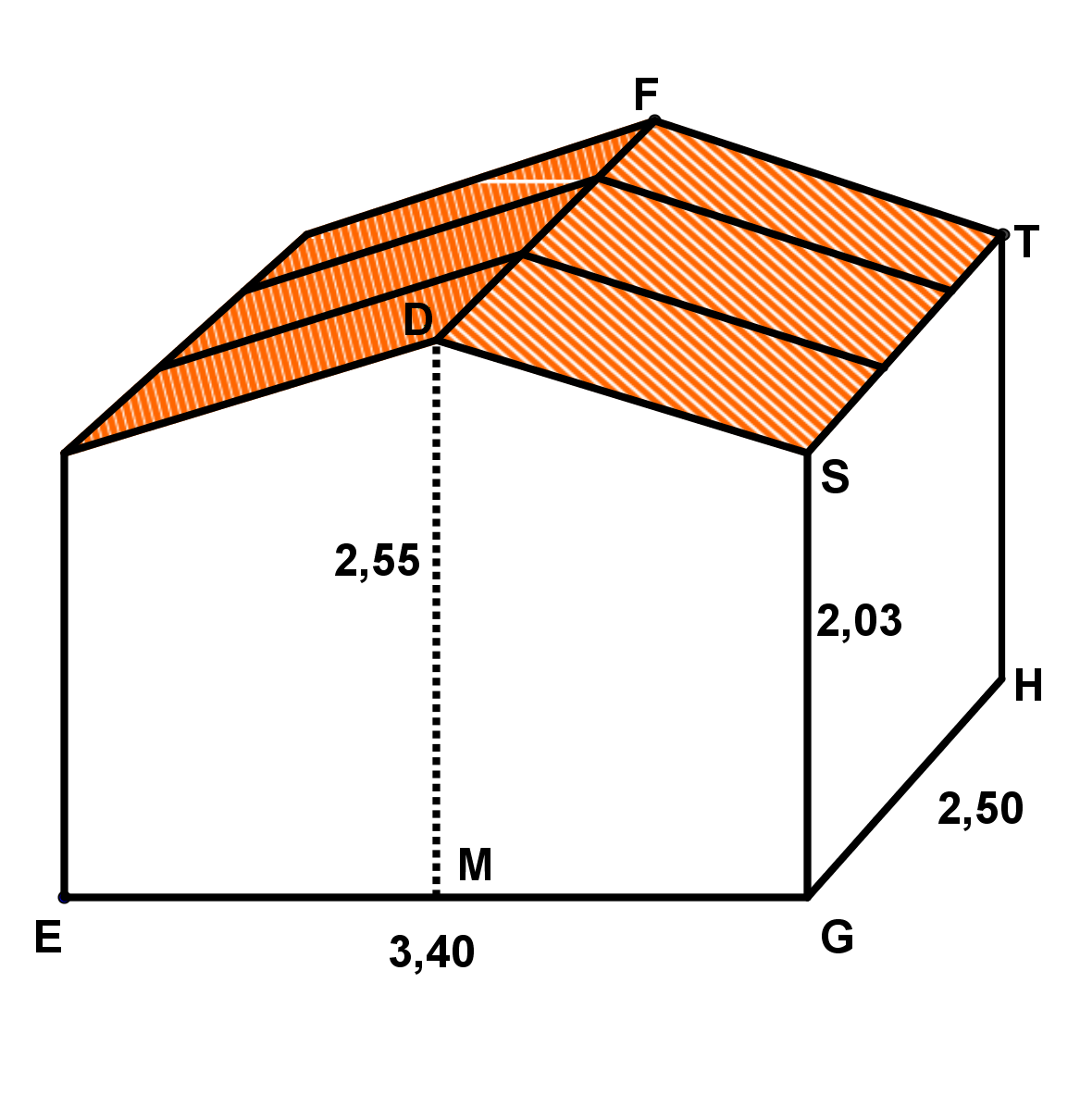
Berechnung der Fläche der Dachhälfte
Das Viereck ist ein Rechteck. Seine Fläche berechnet man daher, indem man zwei aneinander liegende Seiten multipliziert:
Die Streckenlänge ist angegeben, aber musst du noch gesondert berechnen.
Berechnung von :
Die Strecke ist Seite im Dreieck auf der Vorderfläche des Holzhäuschens.
Dieses Dreieck ist bei rechtwinklig. Also kannst du auch in ihm den Satz von Pythagoras anwenden.
Die Hypotenuse ist .

ist halb so lang , und ist in der Aufgabenstellung angegeben.
kannst du ausrechnen als Differenz der Strecken und :
ist angegeben.
kannst du ebenfalls der Aufgabenstellung entnehmen (denn die Strecke ist natürlich genauso lang wie .
Setze dies nun ein.
Diesen gerundeten Wert für kannst du nun für die Berechnung der Dachfläche verwenden.
Berechnung der Dachfläche
Hier setzt du nun und ein.
Der Flächeninhalt des Daches beträgt .
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl → Was bedeutet das?
