Aufgaben zur Satzgruppe des Pythagoras
Hier findest du gemischte Aufgaben zum Satz des Pythagoras. Lerne, den Satz des Pythagoras im rechtwinkligen Dreieck anzuwenden!
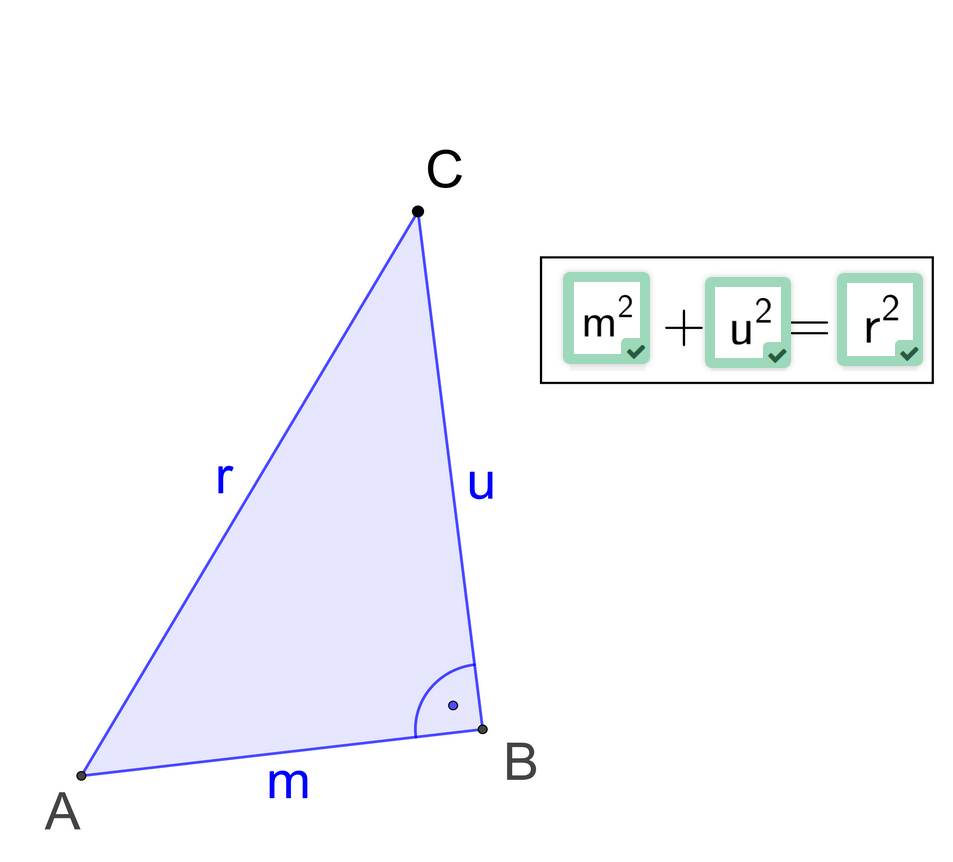
- 1
Der Satz des Pythagoras
Stelle die richtige Gleichung für die Seiten des Dreiecks auf.
- 2
Gib für die rechtwinkligen Dreiecke jeweils die Gleichung nach dem Satz des Pythagoras an.
- 3
Berechne bei den rechtwinkligen Dreiecken die fehlenden Seitenlängen.
- 4
Berechne die Länge der Diagonalen des Rechtecks .
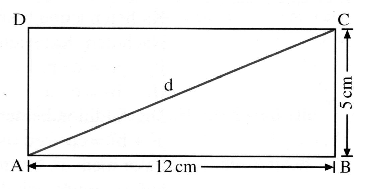 cm
cm - 5
Nach nebenstehender Zeichnung soll ein Doppeltor gebaut werden. Die Maße sind hier jeweils in angegeben. Der Querschnitt der Stäbe ist ein Quadrat mit Kantenlänge .
Berechne die Gesamtlänge an Stäben, die mindestens benötigt wird.
Beachte, wie die Profile zusammengebaut werden.

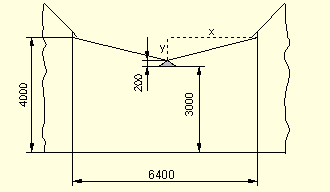
- 6
In der Mitte zwischen zwei Häusern soll an einem Spannseil eine Straßenlaterne aufgehängt werden. Das Spannseil hat genau eine Länge von .
Nachdem die Lampe angebracht wurde, hängt das Seil, wie aus nebenstehender Zeichnung zu sehen ist, etwas durch.
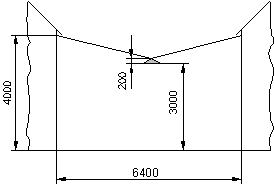
Um welche Länge wurde das Seil durch die Belastung gedehnt?
Wie viel % wird das Seil gedehnt?
- 7
Anwendung in der Physik:
Geschwindigkeitspfeile werden oft zerlegt in Horizontalgeschwidigkeit und Vertikalgeschwindigkeit .
Dabei können und je nach Richtung (rechts/links bzw. oben/unten) positiv oder negativ sein.
Beim Vektor betrachten wir hier die Pfeillänge .
Ergänze die folgende Tabelle
5
6
3
7
12
-8
0,8
15
1
17
5
25
- 8
Nach nebenstehender Zeichnung soll ein Gartentor aus Vierkantprofil () gefertigt werden.
Bestimme die Gesamtlänge der benötigten Profilstäbe, wenn mit einem Verschnitt von zu rechnen ist.
- 9
Wie lang ist die Raumdiagonale in einem Würfel der Kantenlänge 7? Gib das Ergebnis auf eine Nachkommastelle gerundet an!
- 10
Ist das Dreieck mit den Seitenlängen a, b und c rechtwinklig?
a= 3 cm, b=4 cm, c= 5 cm
a= 5 cm, b=13 cm, c=12 cm
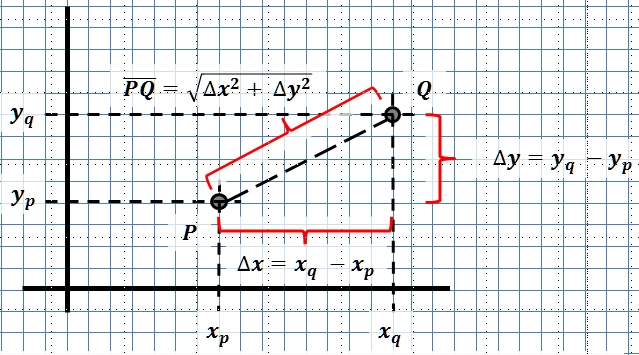
- 11
Löse die folgenden Aufgaben
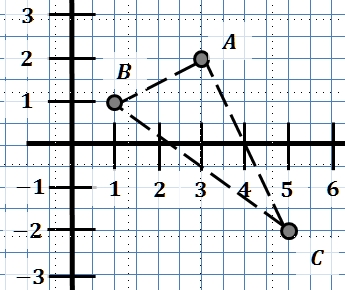
Ermittle die Formel für den Abstand der Punkte und . Mache dir die Formel anhand einer Skizze klar.
Berechne die Seitenlängen des Dreiecks mit , , .
Vom Satz des Pythagoras gilt auch die Umkehrung, d. h., gilt , so hat das Dreieck bei einen rechten Winkel. Zeige damit, dass das Dreieck aus Teilaufgabe b) bei rechtwinklig ist.
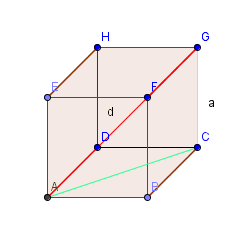
- 12
Betrachte die Planfigur eines rechtwinkligen Dreiecks.
Stelle für die nebenstehende Figur drei Pythagoras-Formeln auf.
Stelle für die nebenstehende Figur drei Pythagoras-Formeln auf.
Im rechtwinkligen Dreieck gilt auch der Kathetensatz (ebenso ), der z. B. mithilfe ähnlicher Dreiecke bewiesen werden kann. Setze damit (und mit Hilfe von Teilaufgabe 1) den hier vorgegebenen Ansatz fort und folgere damit den sogenannten Hohensatz:
- 13
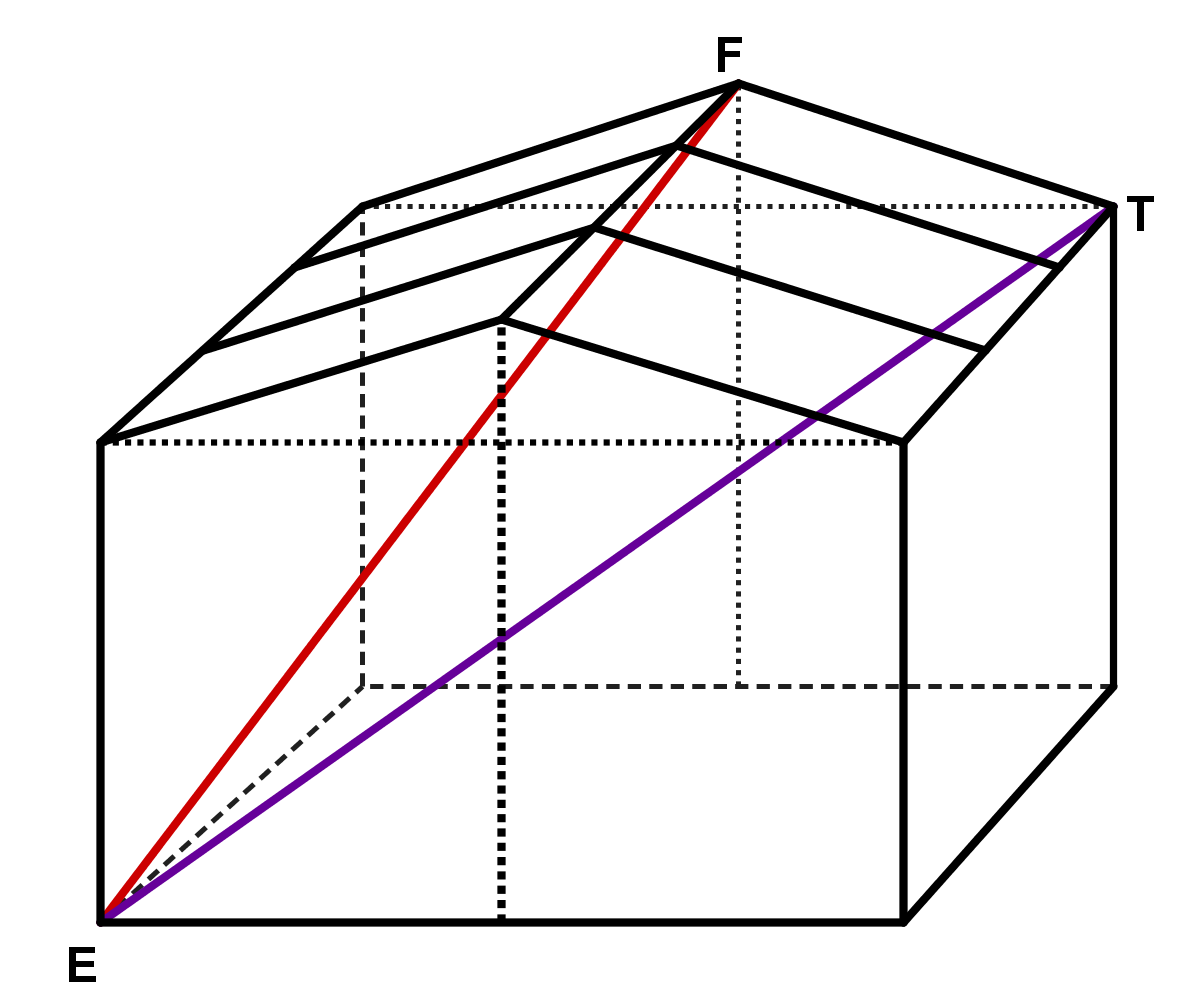
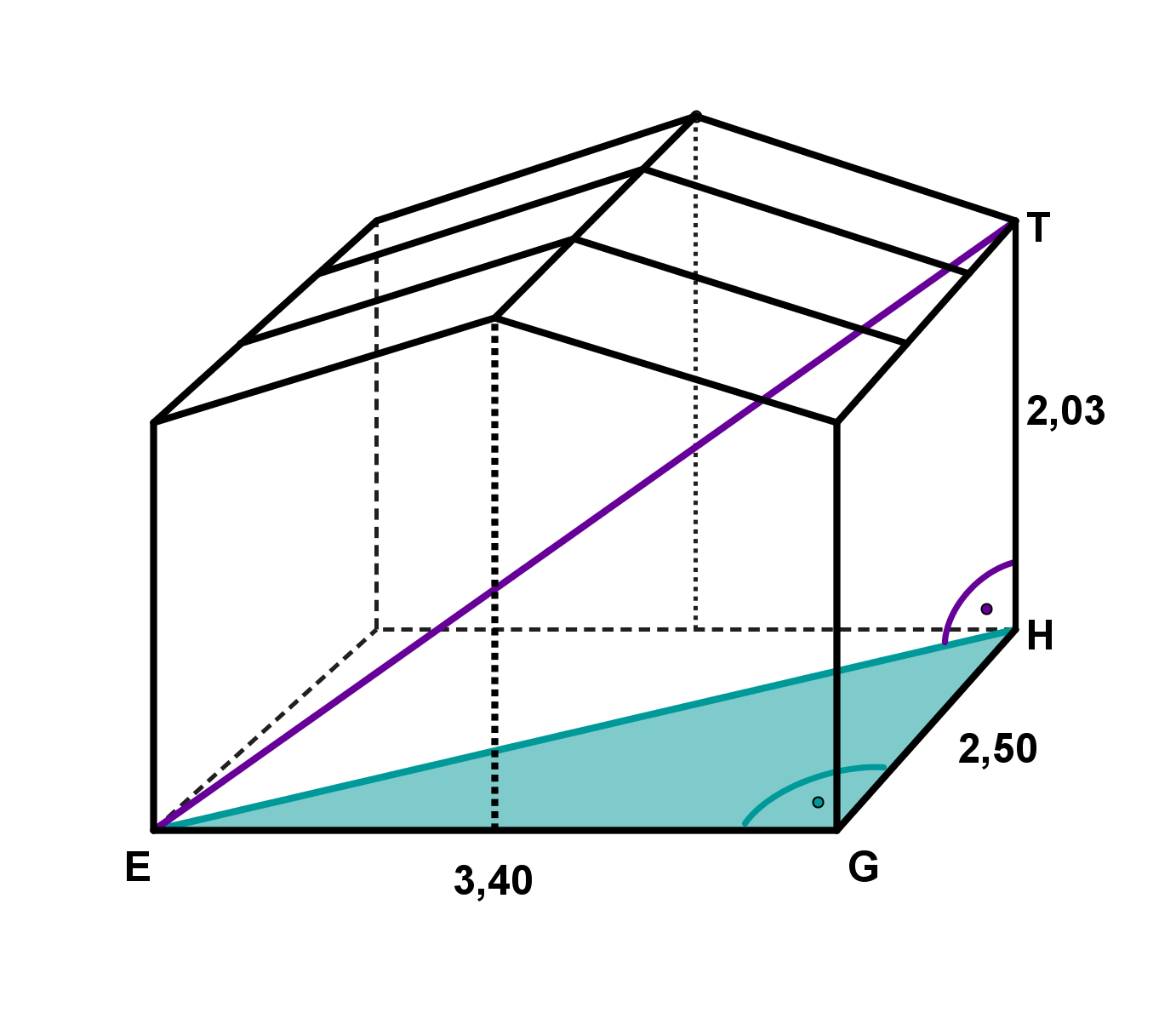
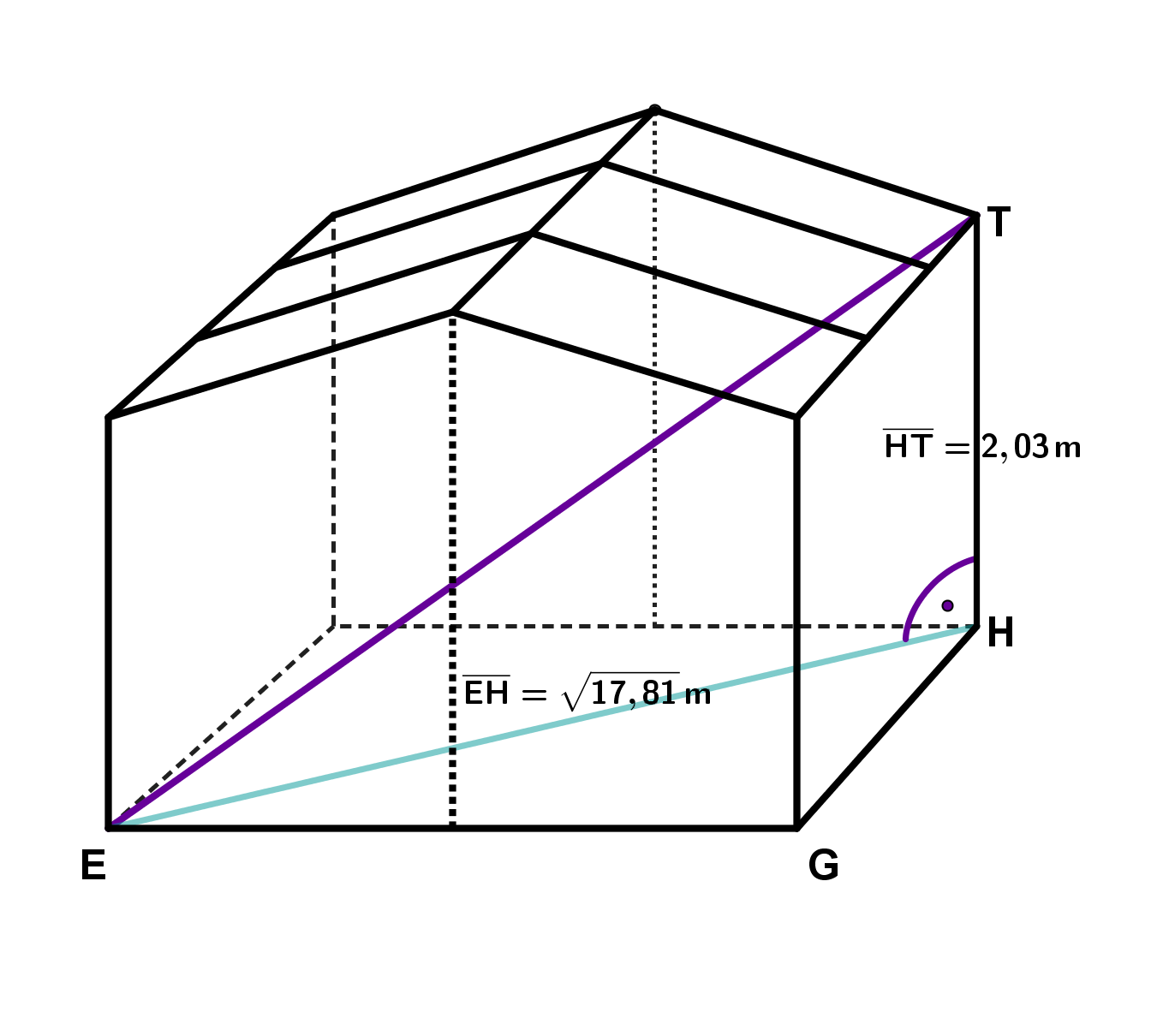
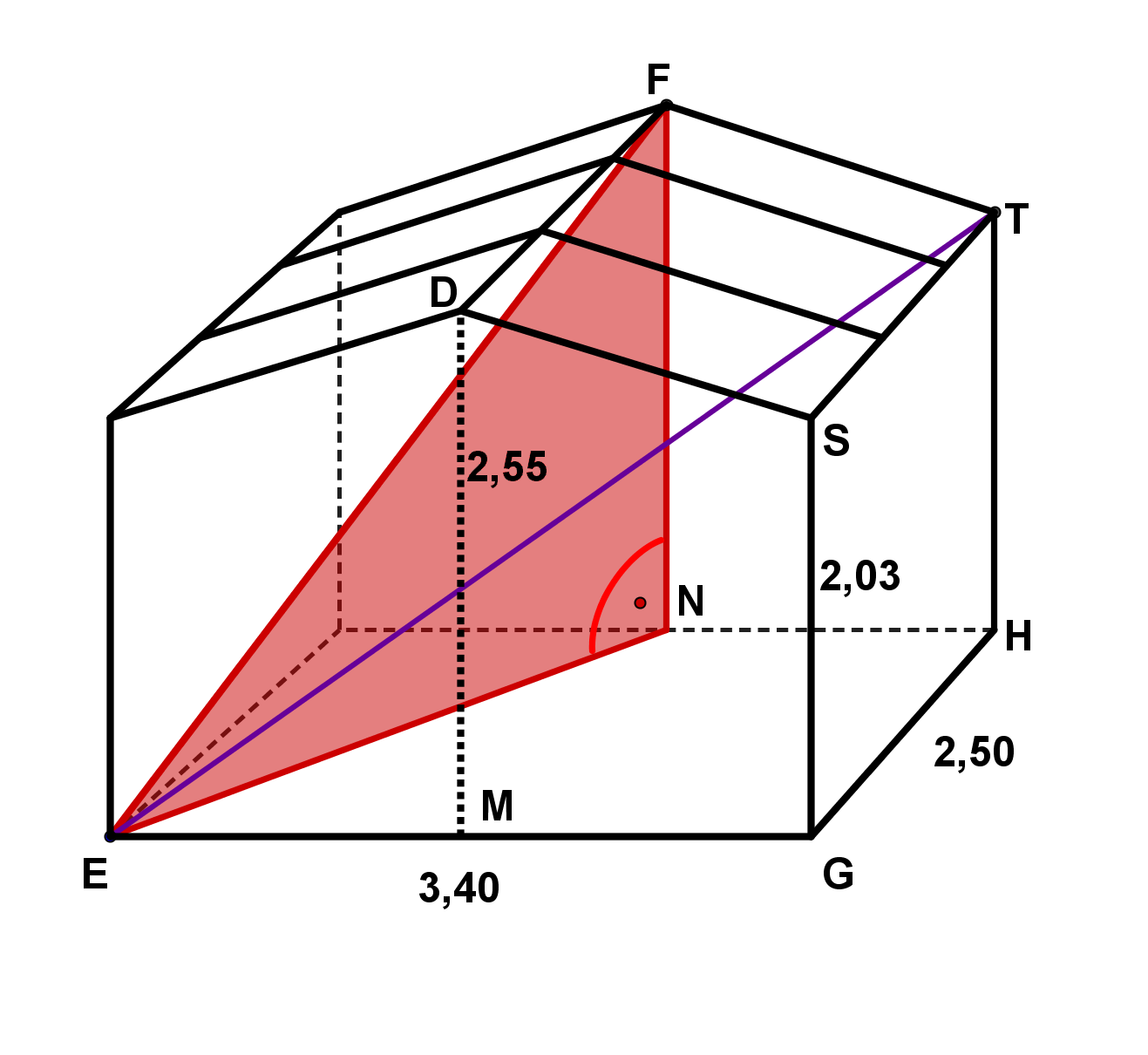
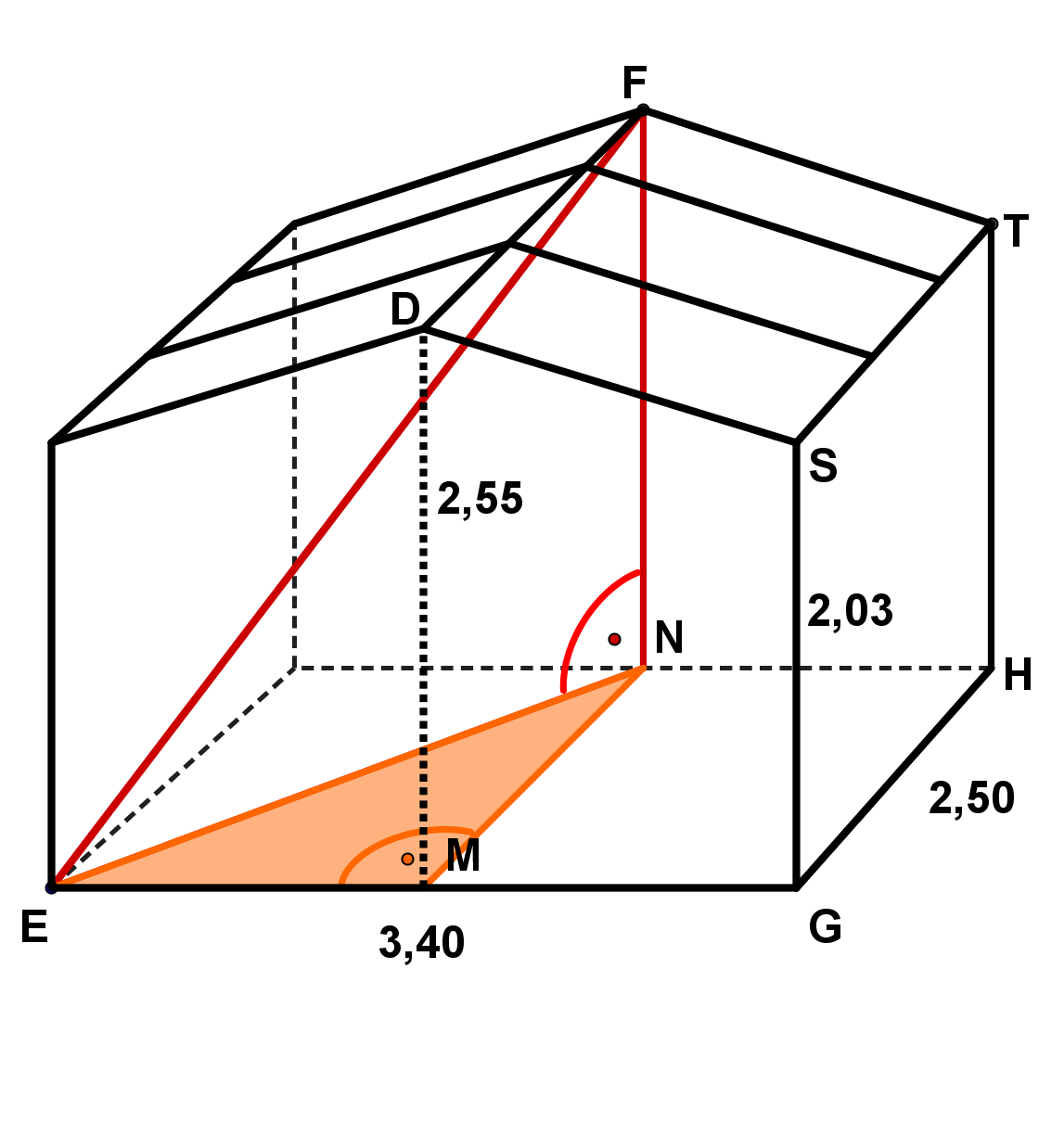
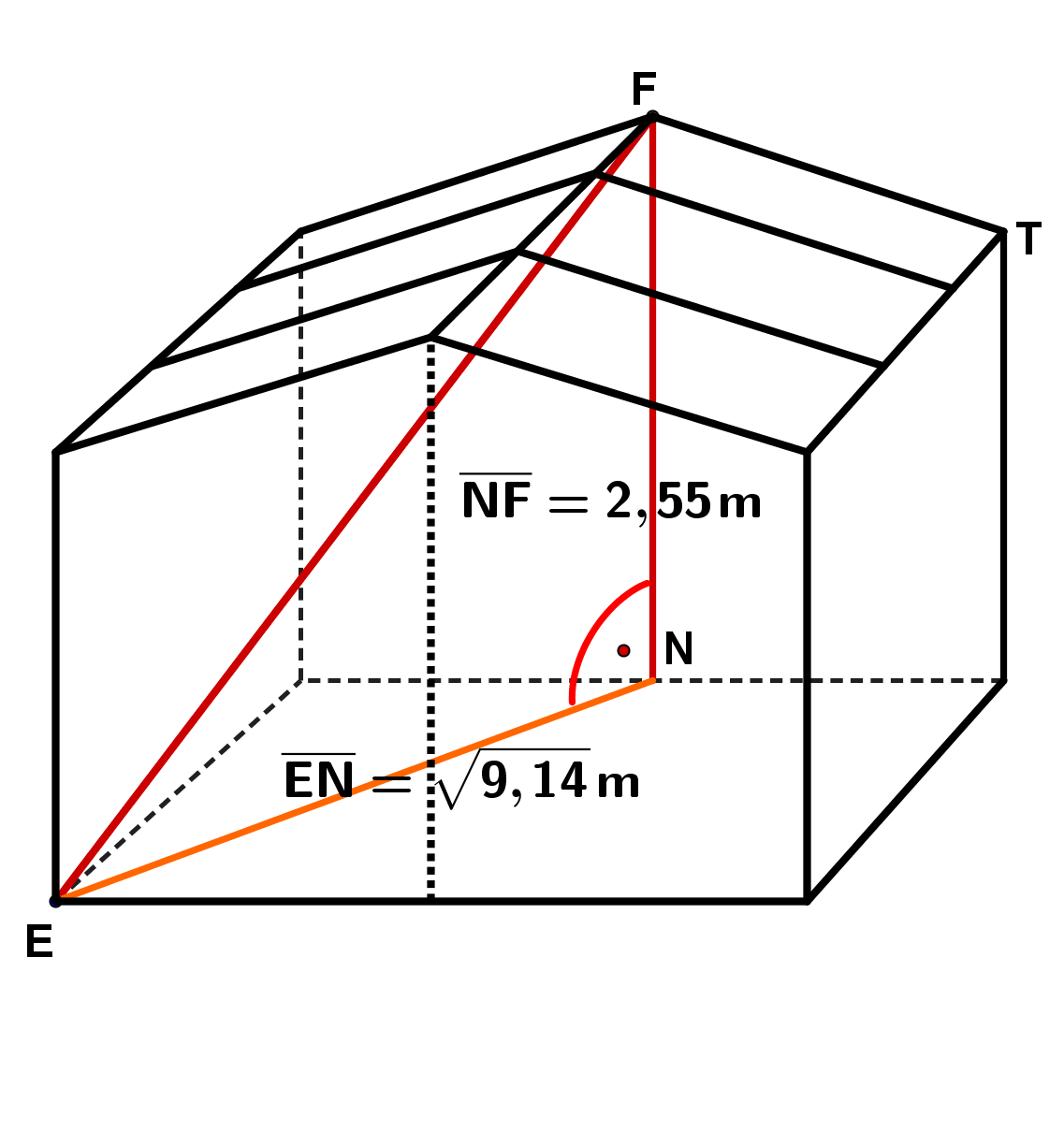
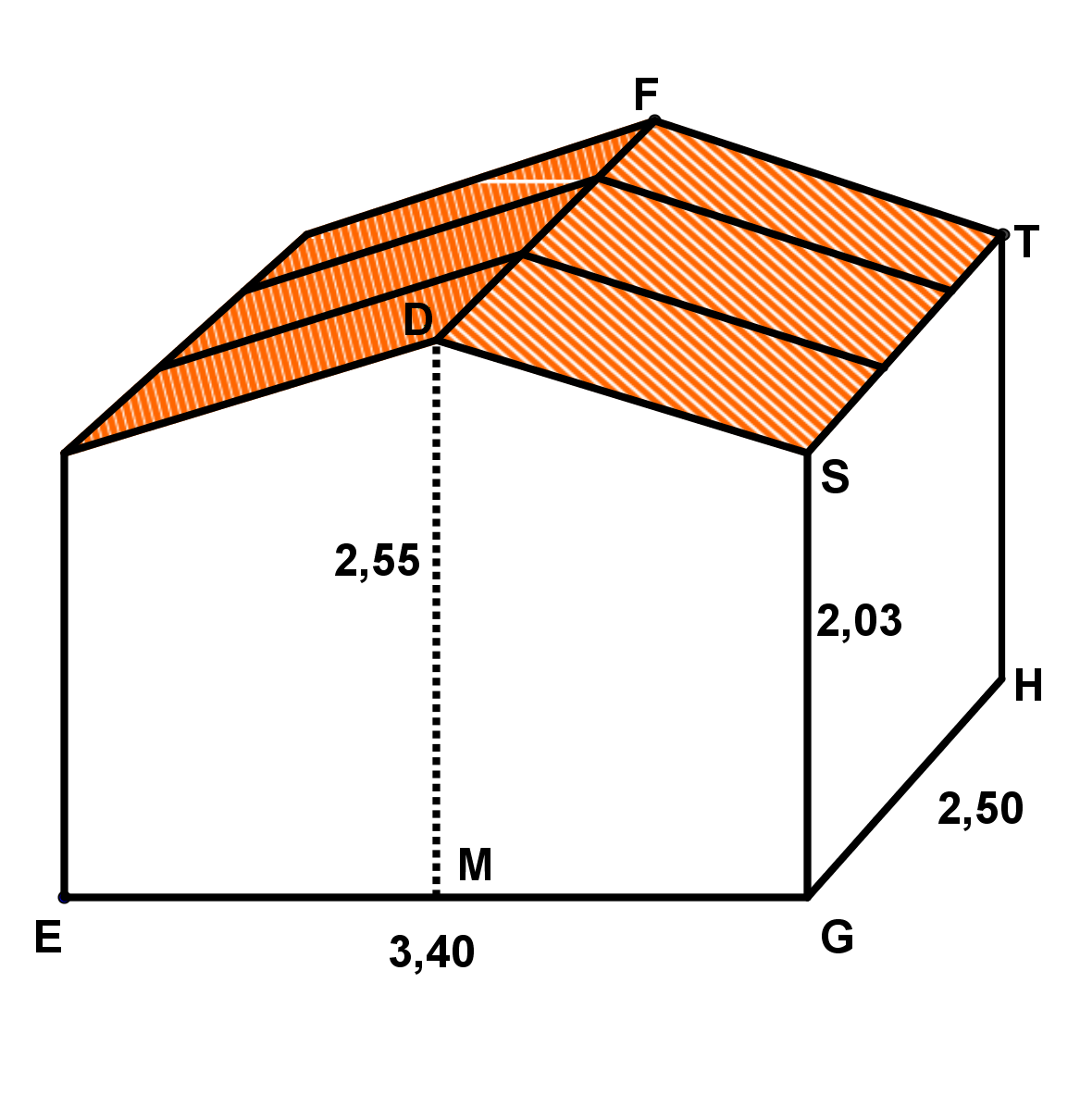
Betrachte folgendes Holzhäuschen (Maße in ):

Wie lang ist der längste Faden, den eine Spinne geradlinig im Holzhäuschen spannen könnte?
Wie viel Dachfläche hat das Holzhäuschen?
- 14
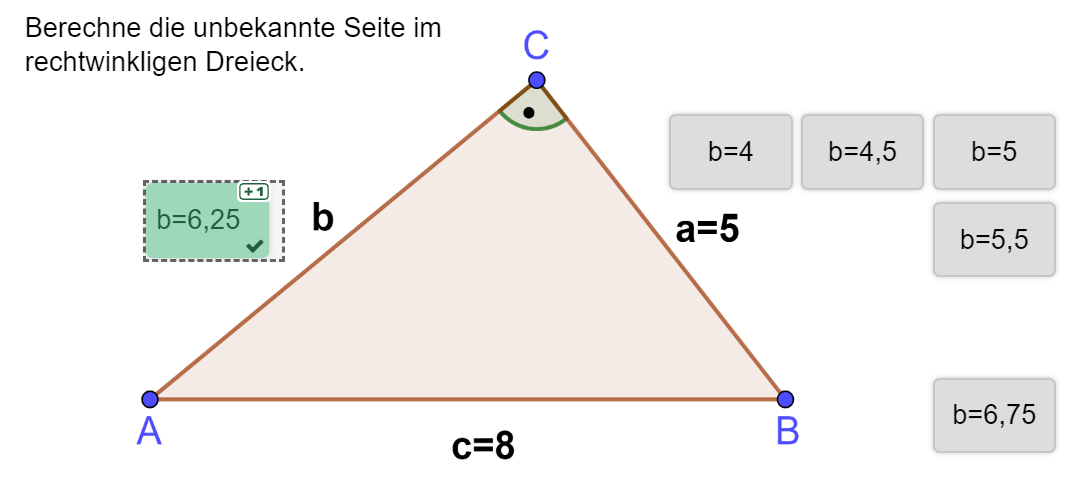
Berechne die unbekannte Seite im rechtwinkligen Dreieck.
- 15
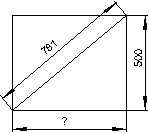
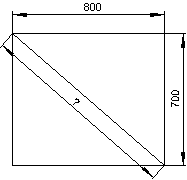
Berechne die fehlenden Längen! (alle Maße in mm)
(Gib die berechnete Länge mit einer Einheit ein.)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?