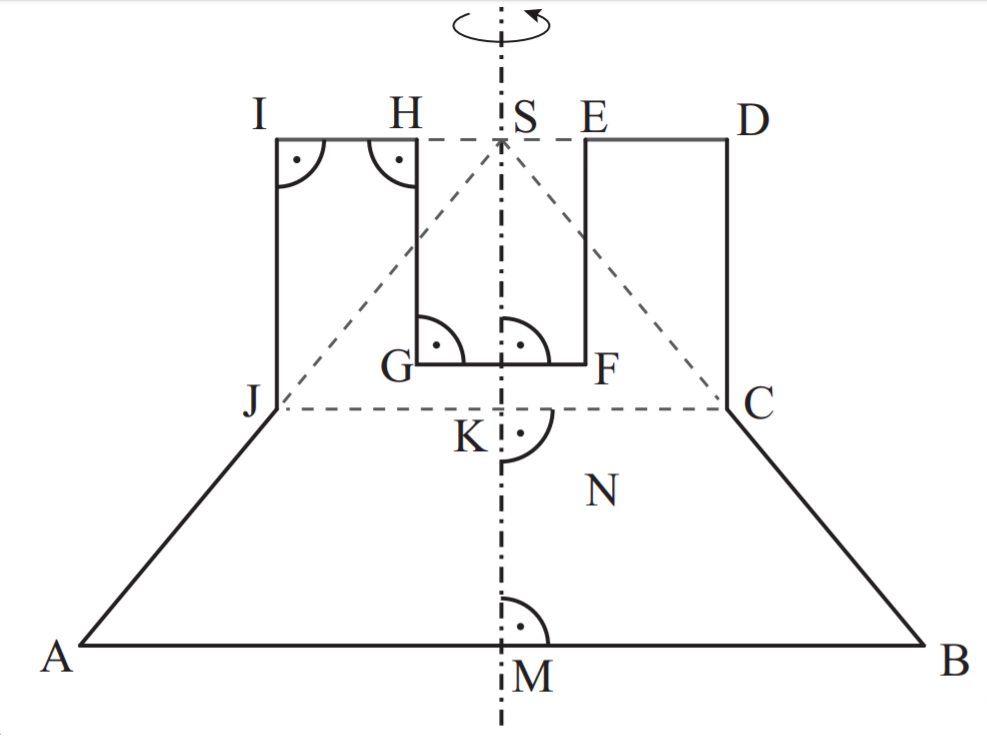
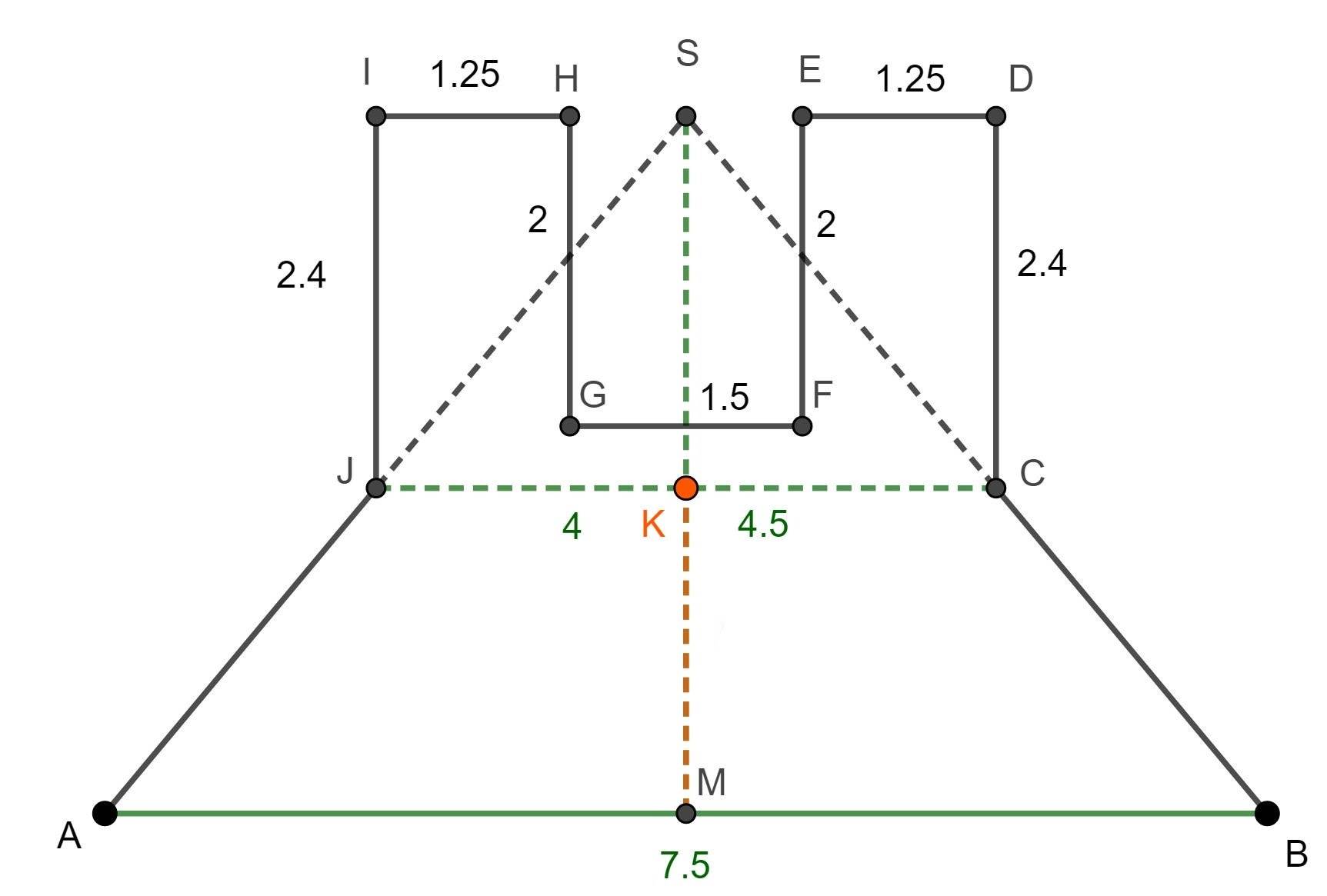
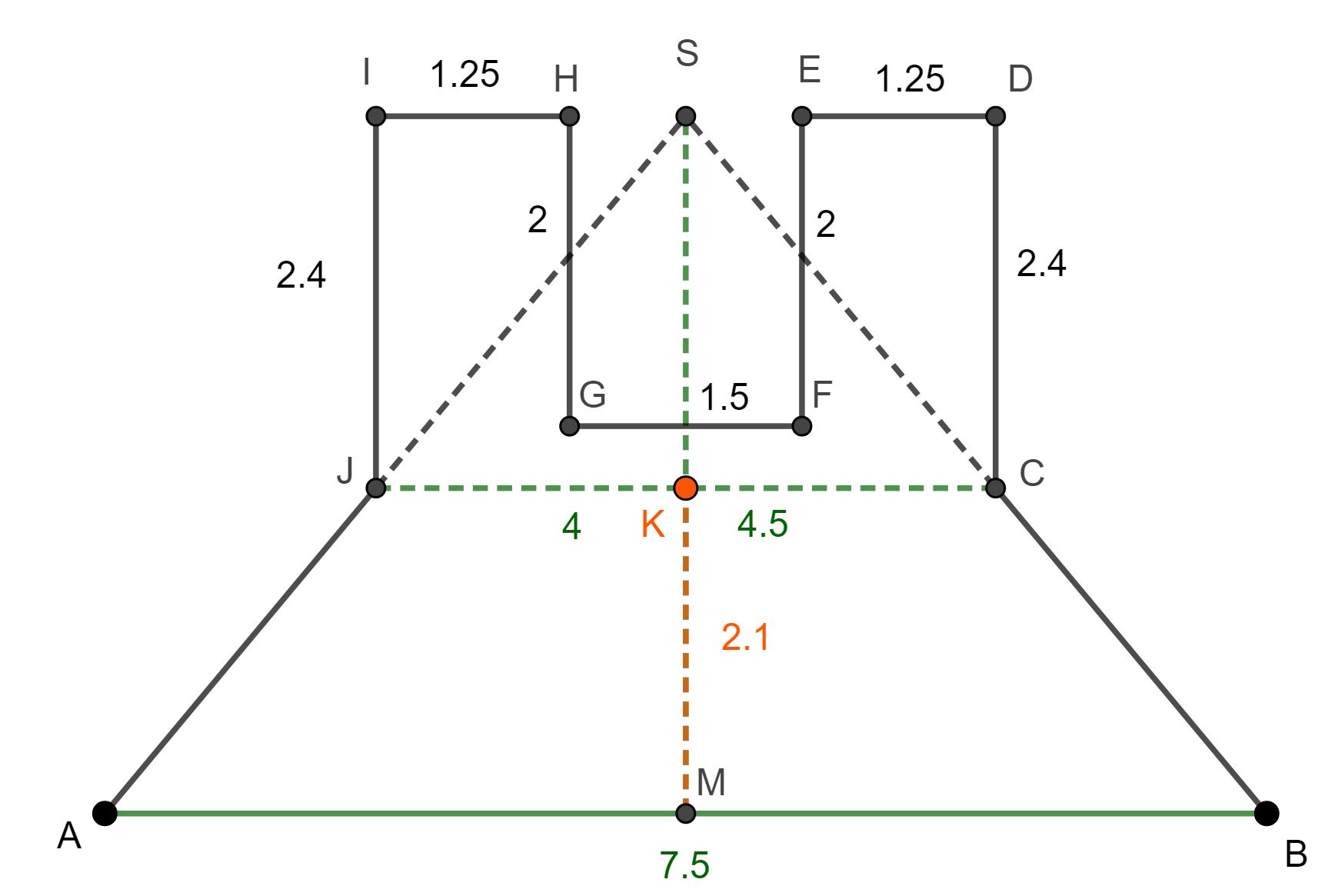
Die Oberfläche des Kerzenständers besteht aus verschiedenen Elementen:
1) Der Mantelfläche des Kegelstumpfs,
2) dem Mantel des "großen", äußeren Zylinders,
3) dem Mantel des "kleinen", inneren Zylinders und
4) zwei Kreisflächen.
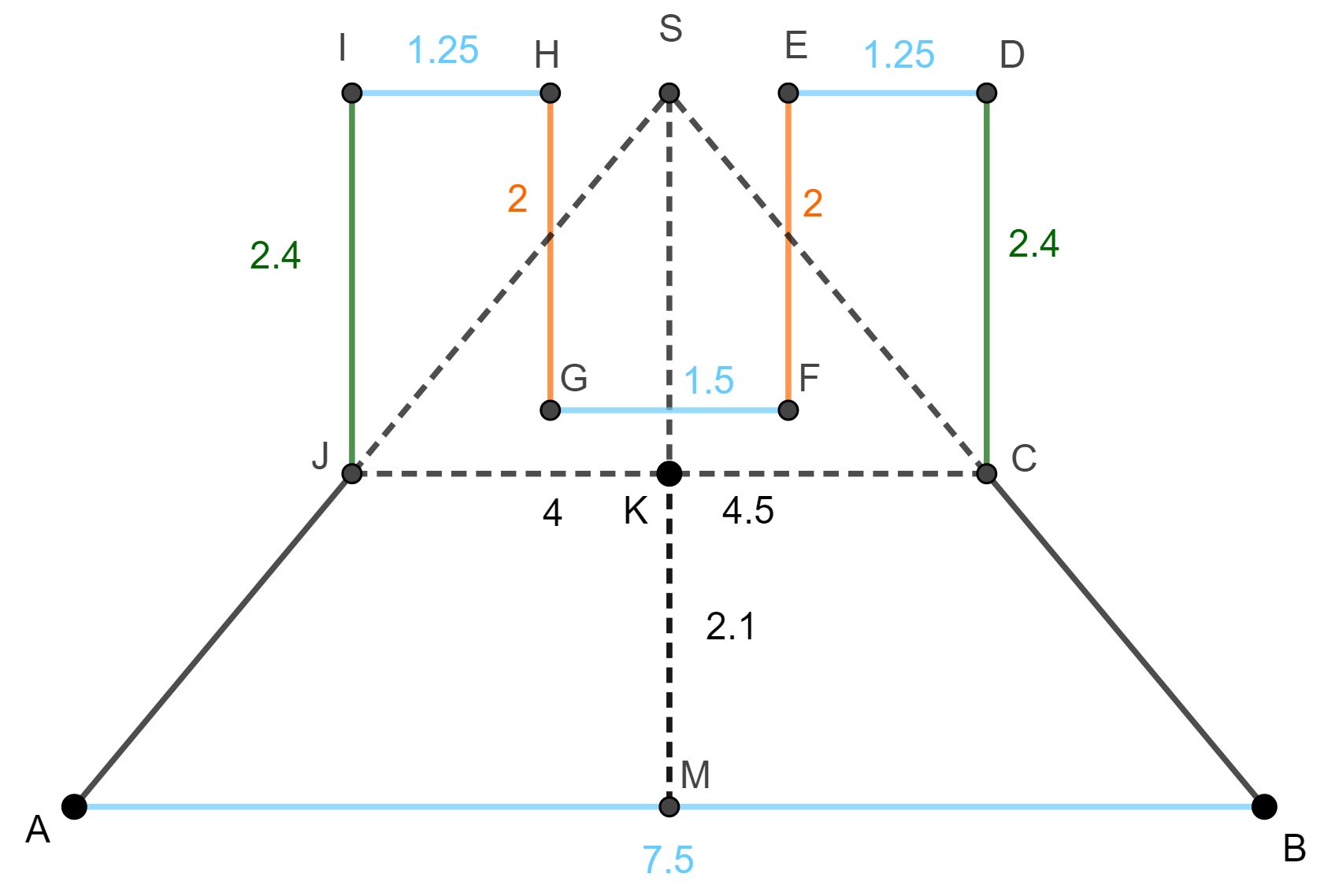
Skizze zu A3.2
1) Zuerst berechnest du die Mantelfläche des Kegelstumpfs.
Da die Formel zur Berechnung lautet, wobei die Mantellinie ist, musst du zunächst die Längen der beiden Mantellinien bestimmen:
und
Nun kannst du die Mantelfläche des "kleinen" vom "großen" Kegel abziehen:
2) Dann berechnest du die Mantelfläche des "äußeren" Zylinders. Dieser besitzt den Radius und die Höhe .
Aus ergibt sich
3) Genauso berechnest du die Mantelfläche des "inneren" Zylinders. Dieser besitzt den Radius und die Höhe .
Dadurch erhältst du
4) Die Kreisflächen sind einerseits der "Fuß" des großen Kegels, also ein Kreis mit Radius .
Setzte dies in die Kreisformel ein, und du erhältst
Die beiden Flächen oben, ein Kreisring und ein kleiner Kreis, ergänzen sich zu einem Kreis mit Radius :
In der Summe erhältst du also
Hinweis: Werden die Oberflächeninhalte auf eine Stelle nach dem Komma gerundet, erhält man auch das Ergebnis .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇