Nachtermin Teil B - lernen mit Serlo!

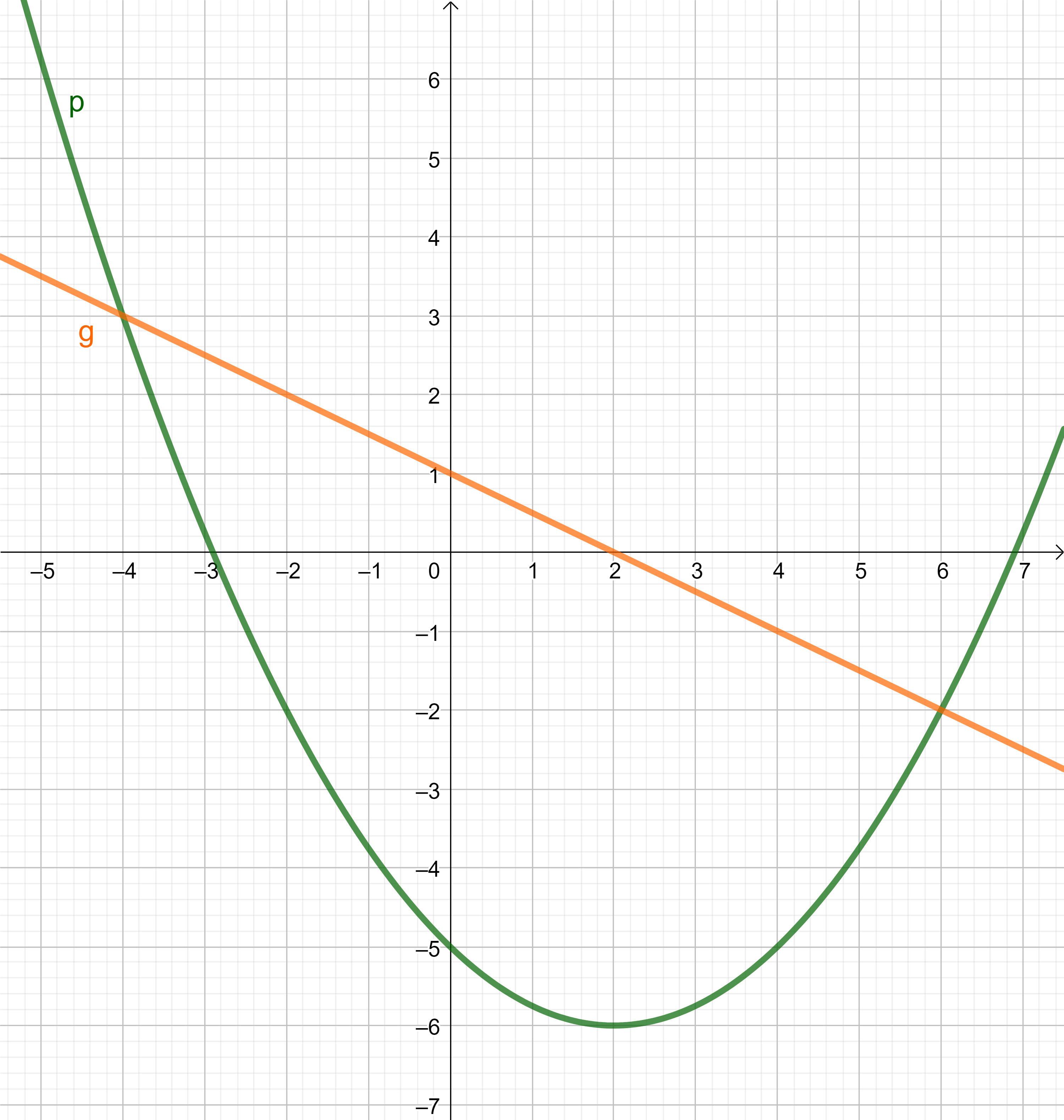
Die Parabel $p$ verläuft durch die Punkte $P (- 6 | 10) und Q (4 | - 5)$ .

Sie hat eine Gleichung der Form $y = 0,25 x^{2} + b x + c mit 𝔾 = ℝ \times ℝ$ und $b, c$ $\in ℝ$ .

Die Gerade $g$ besitzt die Gleichung $y = - 0,5 x + 1 mit 𝔾 = ℝ \times ℝ .$

Zeigen Sie durch Berechnung der Werte für $b$ und $c$ , dass die Parabel $p$ die Gleichung $y = 0,25 x^{2} - x - 5$ besitzt.
Zeichnen Sie sodann die Parabel $p$ und die Gerade $g$ für $x \in [- 5; 7]$ in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit $1$ cm; $- 5 \leq x \leq 7; - 7 \leq y \leq 7$ .

Lösung a
Für diese Aufgabe benötigst du das Grundwissen: Quadratische Funktion
Um die Werte für $b$ und $c$ zu bestimmen, solltest du die Punkte $P$ und $Q$ in die Parabelgleichung $y = a x^{2} + b x + c$ einsetzen. Dann erhältst du zwei Gleichungen mit zwei Unbekannten und kannst das Gleichungssystem lösen.
Erste Gleichung:
Setze $P (x | y) = P (- 6 | 10)$ ein:
$\begin{array}{lrcl} (𝐈) & 10 & = & 0, 25 \cdot {(- 6)}^{2} - 6 b + c \\ 10 & = & 9 - 6 b + c \end{array}$
Zweite Gleichung:
Setze $Q (x | y) = Q (4 | - 5)$ ein:
$\begin{array}{lrcl} (𝐈 𝐈) & - 5 & = & 0, 25 \cdot 4^{2} + 4 b + c \\ - 5 & = & 4 + 4 b + c \end{array}$
Jetzt kannst du zum Beispiel die erste Gleichung nach $c$ auflösen:
$\begin{array}{ccclr} (𝐈) & 10 & = & 9 - 6 b + c & | - 9; + 6 b \\ 1 + 6 b & = & c \end{array}$
Setze $c$ in die zweite Gleichung ein:
$\begin{array}{lrclll} (𝐈 𝐈) & - 5 & = & 4 + 4 b + 1 + 6 b \\ - 5 & = & 5 + 10 b & | & - 5 \\ - 10 & = & 10 b & | & : 10 \\ - 1 & = & b \end{array}$
Jetzt kennst du schon den Wert von $b$ . Setze ihn nun wieder in die erste Gleichung ein und du kannst auch $c$ bestimmen:
$\begin{array}{crcl} (𝐈) & 1 + 6 b & = & c \\ 1 - 6 & = & c \\ - 5 & = & c \end{array}$
Eingesetzt in die Parabelgleichung erhältst du das Ergebnis:
$p : y = 0,25 x^{2} - x - 5$
Als Letztes sollst du $p$ noch zusammen mit der Geraden $g$ in ein Koordinatensystem zeichnen, das könnte so aussehen:
Parabel mit Gerade
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
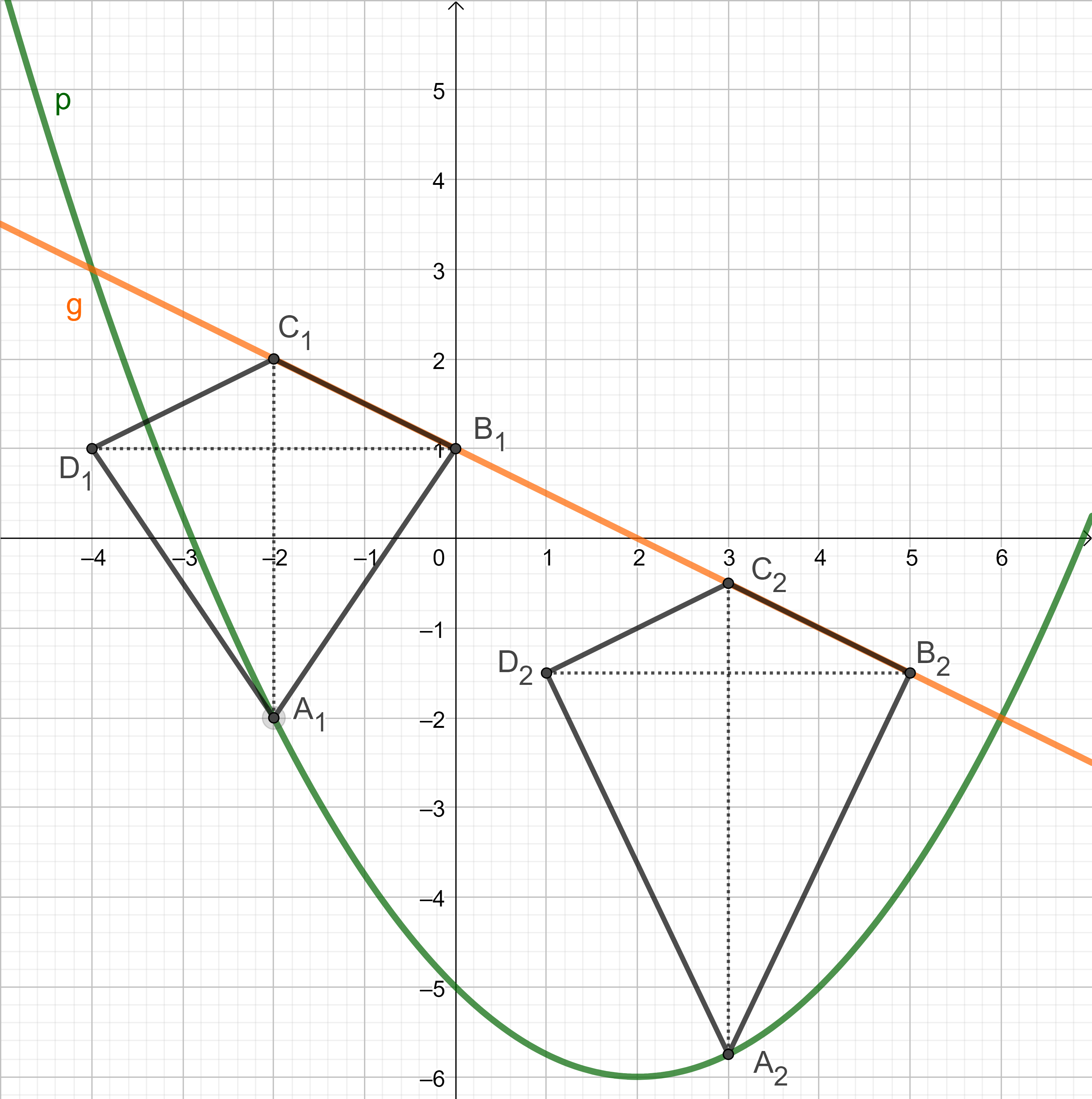
Punkte $A_{n} (x | 0,25 x^{2} - x - 5)$ auf der Parabel $p$ und Punkte $C_{n} (x | - 0,5 x + 1$ ) auf der Geraden $g$ haben dieselbe Abszisse $x$ . Sie sind zusammen mit Punkten $B_{n}$ auf der Geraden $g$ und Punkten $D_{n}$ für $x \in] - 4; 6 [$ Eckpunkte von Drachenvierecken $A_{n} B_{n} C_{n} D_{n}$ mit der Geraden $A_{n} C_{n}$ als Symmetrieachse. Der Abstand der Punkte $B_{n}$ von der Geraden $A_{n} C_{n}$ beträgt $2$ LE.
Zeichnen Sie die Drachenvierecke $A_{1} B_{1} C_{1} D_{1}$ für $x = - 2$ und $A_{2} B_{2} C_{2} D_{2}$ für $x = 3$ in das Koordinatensystem zu Teilaufgabe a) ein.

Lösung b
Um das Drachenviereck $A_{1} B_{1} C_{1} D_{1}$ einzuzeichnen, gehst du auf der $x$ -Achse zur Stelle $x = - 2$ . Dort gehst du dann senkrecht nach oben und zeichnest auf die Gerade $g$ den Punkt $C_{1}$ .
Wenn du von $x = - 2$ senkrecht nach unten gehst, kannst du auf der Parabel $p$ den Punkt $A_{1}$ einzeichnen.
Da der Punkt $B_{1}$ den Abstand $2$ zu $[A_{1} C_{1}]$ hat, musst du für $B_{1}$ auf der $x$ -Achse $2$ Schritte nach rechts, also zur Stelle $x = 0$ , gehen und den Punkt $B_{1}$ dann dort auf der Gerade $g$ einzeichnen.
Da es sich um ein Drachenviereck handelt, hat auch der Punkt $D_{1}$ einen Abstand von $2$ zu $[A_{1} C_{1}]$ , liegt aber links davon, also an der Stelle $x = - 4$ . Der $y$ -Wert von $D_{1}$ ist dann derselbe, den auch $B_{1}$ besitzt.
Zum Schluss musst du nur noch die Punkte miteinander verbinden.
Beim Drachenviereck $A_{2} B_{2} C_{2} D_{2}$ kannst du dann genauso vorgehen.
Insgesamt sieht die Zeichnung dann so aus:
Drachenvierecke zwischen Parabel und Gerade
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Geben Sie die Koordinaten der Punkte $D_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $A_{n}$ an.

Lösung c
Die Strecke $[A_{n} C_{n}]$ halbiert die Strecke $B_{n} D_{n}$ , wenn also $B_{n}$ einen Abstand von $2$ LE zu $[A_{n} C_{n}]$ hat, dann hat auch $D_{n}$ einen Abstand von $2$ LE zu $[A_{n} C_{n}]$ . Die $x$ -Koordinate von $D_{n}$ erhältst du also, wenn du von der Abszisse von $A_{n}$ um $2$ Schritte in negative $x$ -Richtung gehst, sie ist also $x_{D_{n}} = x - 2$ .
Die $y$ -Koordinate von $D_{n}$ entspricht der $y$ -Koordinate von $B_{n}$ . Du weißt, dass der Punkt $B_{n}$ die Abszisse $x_{B_{n}} = x + 2$ hat und auf der Geraden $g$ liegt, seine $y$ -Koordinate findest du also heraus, indem du $x + 2$ in die Geradengleichung einsetzt:
$\begin{array}{rclcl} y_{D_{n}} & = & y_{B_{n}} & = & - 0,5 \cdot (x + 2) + 1 \\ = & - 0,5 x - 1 + 1 \\ = & - 0,5 x \end{array}$
Damit hast du jetzt also die folgenden Koordinaten:
$D_{n} (x - 2 | - 0,5 x)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Ermitteln Sie durch Rechnung den Flächeninhalt $A$ der Drachenvierecke $A_{n} B_{n} C_{n} D_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $A_{n}$ .
$[Teilergebnis: A_{n} C_{n} (x) = (- 0,25 x^{2} + 0,5 x + 6) LE]$

Lösung d
Für diese Aufgabe benötigst du das Grundwissen: Flächeninhalt eines Drachenvierecks
Um den Flächeninhalt eines Drachenvierecks zu berechnen, benötigst du die Längen seiner Diagonalen. Das Drachenviereck $A_{n} B_{n} C_{n} D_{n}$ hat die Diagonalen $[A_{n} C_{n}]$ und $[B_{n} D_{n}]$ , in diesem Fall ist der Flächeninhalt also:
$A_{A_{n} B_{n} C_{n} D_{n}} = \frac{1}{2} \cdot B_{n} D_{n} \cdot A_{n} C_{n}$
Die Länge der Strecke $[B_{n} D_{n}]$ kennst du schon, sie hat den Wert $4$ LE.
Um die Länge der Strecke $[A_{n} C_{n}]$ zu berechnen, solltest du bedenken, dass die Punkte $A_{n}$ und $C_{n}$ dieselbe Abszisse $x$ haben. Der Abstand zwischen den beiden entspricht also dem Abstand der $y$ -Koordinaten der Punkte, dieser ist einfach die Differenz, also:
$\begin{array}{rclll} A_{n} C_{n} & = & y_{C_{n}} - y_{A_{n}} & = & [- 0,5 x + 1 - (0,25 x^{2} - x - 5)] LE \\ = & [- 0,5 x + 1 - 0,25 x^{2} + x + 5] LE \\ = & [- 0,25 x^{2} + 0,5 x + 6] LE \end{array}$
Damit hast du jetzt auch die Länge der zweiten Diagonalen bestimmt. Nun kannst du den Flächeninhalt des Drachenvierecks berechnen:
$\begin{array}{ccl} A_{A_{n} B_{n} C_{n} D_{n}} & = & 0,5 \cdot B_{n} D_{n} \cdot A_{n} C_{n} \\ = & 0,5 \cdot 4 LE \cdot (- 0,25 x^{2} + 0,5 x + 6) LE \\ = & (- 0,5 x^{2} + x + 12) FE \end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Unter den Drachenvierecken $A_{n} B_{n} C_{n} D_{n}$ gibt es das Drachenviereck $A_{0} B_{0} C_{0} D_{0}$ , das die größtmögliche Streckenlänge $A_{0} C_{0}$ besitzt. Bestimmen Sie rechnerisch die Länge der Strecke $[A_{0} C_{0}]$ sowie die Koordinaten des Punktes $B_{0}$ .

Lösung e
Für diese Aufgabe benötigst du das Grundwissen: Scheitelpunkt einer Parabel
In dieser Aufgabe geht es darum, die Länge der Strecke $[A_{n} C_{n}]$ zu maximieren, du musst also eine Extremwertaufgabe lösen.
In Teilaufgabe d hast du bereits eine Formel für die Länge dieser Strecke bestimmt:
$A_{n} C_{n} (x) = - 0,25 x^{2} + 0,5 x + 6$
Dabei handelt es sich um eine quadratische Funktion, ihr Graph ist eine nach unten geöffnete Parabel. Das Maximum der Länge kannst du ablesen, wenn du den Scheitelpunkt der Funktion kennst. Diesen kannst du entweder mit der Formel oder mit quadratischer Ergänzung bestimmen.
Bestimmen des Scheitels mit der Formel
Die Formel für den Scheitelpunkt ist: $S (- \frac{b}{2 \cdot a} | c - \frac{b^{2}}{4 \cdot a})$ , wenn du eine quadratische Funktion in der allgemeinen Form $f (x) = a x^{2} + b x + c$ gegeben hast. Das ist hier der Fall, du musst nur noch durch Vergleichen die Werte von $a, b$ und $c$ bestimmen:
Hier gilt $a = - 0,25$ , $b = 0,5$ und $c = 6$ . Diese Werte musst du jetzt nur noch einsetzen und erhältst:
$S (- \frac{0,5}{2 \cdot (- 0,25)} | 6 - \frac{{0,5}^{2}}{4 \cdot (- 0,25)}) \Rightarrow S (1 | 6,25)$
Die größtmögliche Streckenlänge $A_{0} C_{0}$ entspricht der y-Koordinate des Scheitelpunkts, also $6,25 LE$ .
Zusätzlich gibt dir der Scheitelpunkt auch die Abszisse $x = 1$ der zugehörigen Punkte $A_{0}$ und $C_{0}$ an. Die Abszisse des Punkts $B_{0}$ ist dann $x_{B_{0}} = 1 + 2 = 3$ . Da $B_{0}$ auf der Geraden $g$ liegt, kannst du diesen Wert einfach in die Geradengleichung einsetzen und erhältst auch die y-Koordinate von $B_{0}$ :
$\begin{array}{rcl} y & = & - 0,5 x + 1 \\ = & - 0,5 \cdot 3 + 1 \\ = & - 0,5 \end{array}$
Damit hast du nun beide Koordinaten von $B_{0} (3 | - 0,5)$ bestimmt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Unter den Drachenvierecken $A_{n} B_{n} C_{n} D_{n}$ gibt es die Drachenvierecke $A_{3} B_{3} C_{3} D_{3}$ und $A_{4} B_{4} C_{4} D_{4}$ , für die gilt: $A_{n} C_{n} = 1,5 \cdot B_{n} D_{n}$ . Berechnen Sie die $x$ -Koordinaten der Punkte $A_{3}$ und $A_{4}$ .

Lösung f
Die Punkte $B_{n}$ haben immer einen Abstand von $2 LE$ zur Strecke $A_{n} C_{n}$ . Für die Punkte $D_{n}$ gilt das gleiche, da sie einfach auf der anderen Seite der Strecke liegen. Die Strecke $B_{n} D_{n}$ ist also immer $4 LE$ lang.
Für die Drachenvierecke $A_{3} B_{3} C_{3} D_{3}$ und $A_{4} B_{4} C_{4} D_{4}$ muss also gelten:
$A_{n} C_{n} = 1,5 \cdot 4 LE = 6 LE$
Setze jetzt die Formel für die Länge der Strecke $A_{n} C_{n}$ ein und du erhältst eine Gleichung, die du nach $x$ auflösen kannst:
$\begin{array}{rclcll} - 0,25 x^{2} + 0,5 x + 6 & = & 6 & | & - 6 \\ - 0,25 x^{2} + 0,5 x & = & 0 \end{array}$
Klammere jetzt $x$ aus:
$x (- 0,25 x + 0,5) = 0$
Auf der linken Seite der Gleichung stehen jetzt $2$ Faktoren, damit am Ende $0$ herauskommt, muss also einer der beiden Faktoren selbst $0$ sein.
Die erste Lösung ist also $x = 0$
Für die zweite Lösung schaust du dir den anderen Faktor an und setzt ihn gleich $0$ :
$\begin{array}{rclll} - 0,25 x + 0,5 & = & 0 & | & + 0,25 x \\ 0,5 & = & 0,25 x & | & : 0,25 \\ 2 & = & x \end{array}$
Damit ist die zweite mögliche Lösung $x = 2$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Begründen Sie, dass das Maß der Winkel $C_{n} B_{n} D_{n}$ für alle Drachenvierecke $A_{n} B_{n} C_{n} D_{n}$ gleich ist.

Lösung g
Der Winkel $C_{n} B_{n} D_{n}$ wird am Punkt $B_{n}$ von den Strecken $[B_{n} C_{n}]$ und $[B_{n} D_{n}]$ aufgespannt. Die Strecke $[B_{n} C_{n}]$ liegt dabei auf der Geraden $g$ , während die Strecke $[B_{n} D_{n}]$ parallel zur x-Achse verläuft.
Das Maß des Winkels entspricht also dem Maß des Winkels zwischen $g$ und der x-Achse. Dieser Winkel hat aber immer dasselbe Maß und deshalb ist auch das Maß von $∠ C_{n} B_{n} D_{n}$ für alle Drachenvierecke $A_{n} B_{n} C_{n} D_{n}$ gleich.
Im folgenden Applet kannst du dir das nochmal veranschaulichen, in dem du das Drachenviereck mithilfe des Schiebereglers veränderst.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇