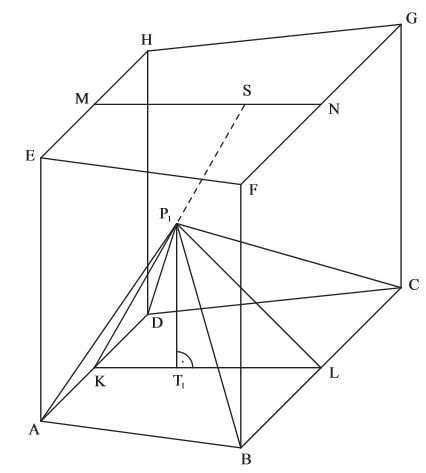
Das gleichschenklige Trapez hat die parallelen Seiten und . Der Mittelpunkt der Seite ist der Punkt , der Mittelpunkt der Seite ist der Punkt . Das Trapez ist die Grundfläche des geraden Prismas (siehe Skizze). Der Punkt liegt senkrecht über dem Punkt .
Es gilt: ; ; ;
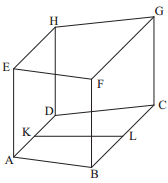
Zeichnen Sie ein Schrägbild des Prismas , wobei auf der Schrägbildachse und der Punkt links vom Punkt liegen soll.
Für die Zeichnung gilt: .
Der Mittelpunkt der Kante ist der Punkt , der Mittelpunkt der Kante ist der Punkt . Für den Punkt auf gilt: .
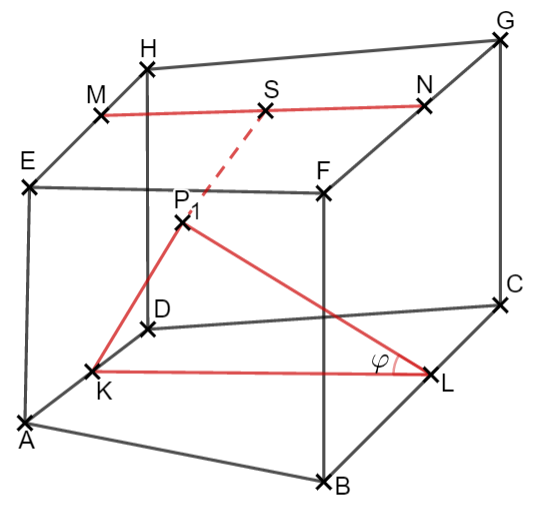
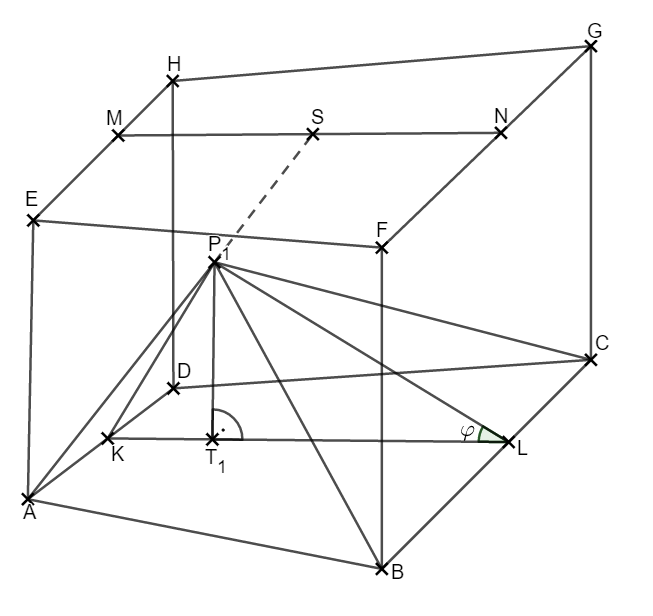
Punkte auf bilden zusammen mit den Punkten und die Dreiecke . Die Winkel haben das Maß mit
Zeichnen Sie die Strecke , den Punkt sowie das Dreieck für in das Schrägbild zur Aufgabenstellung (a) ein.
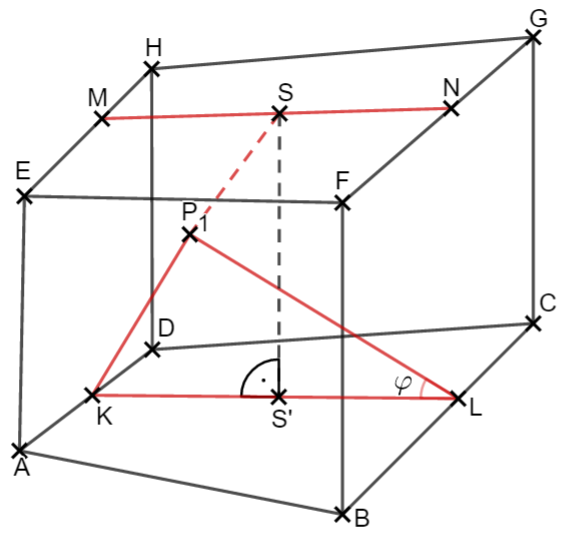
Bestätigen Sie rechnerisch, dass der Winkel das Maß hat.
Zeigen Sie durch Rechnung, dass für die Länge der Strecken in Abhängigkeit von gilt:
Geben Sie die minimale Länge der Strecken an.
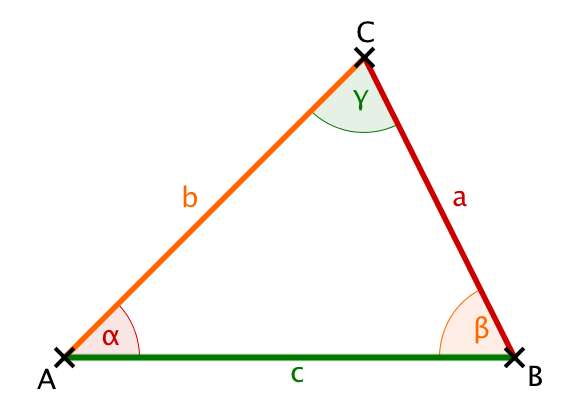
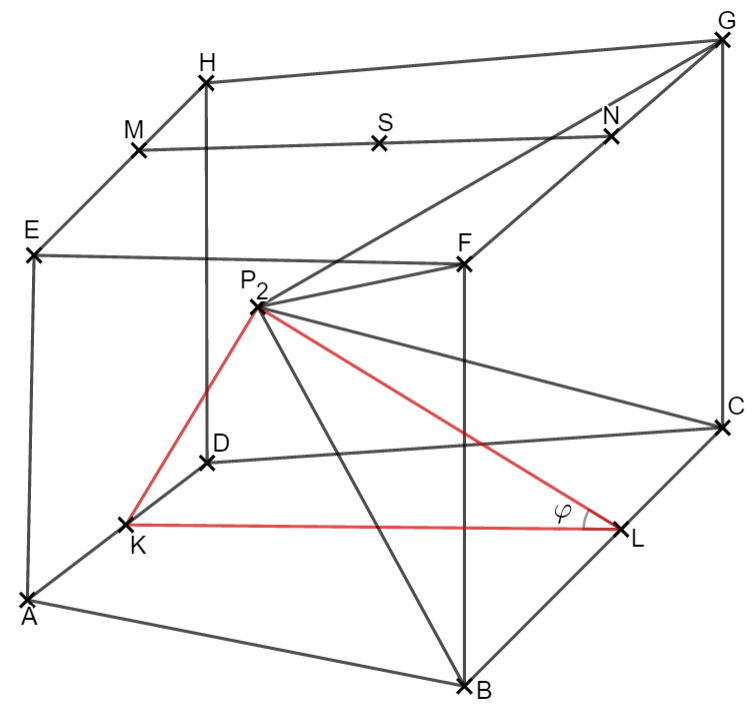
Unter den Dreiecken gibt es das gleichschenklige Dreieck mit der Basis . Berechnen Sie die Länge der Strecke .
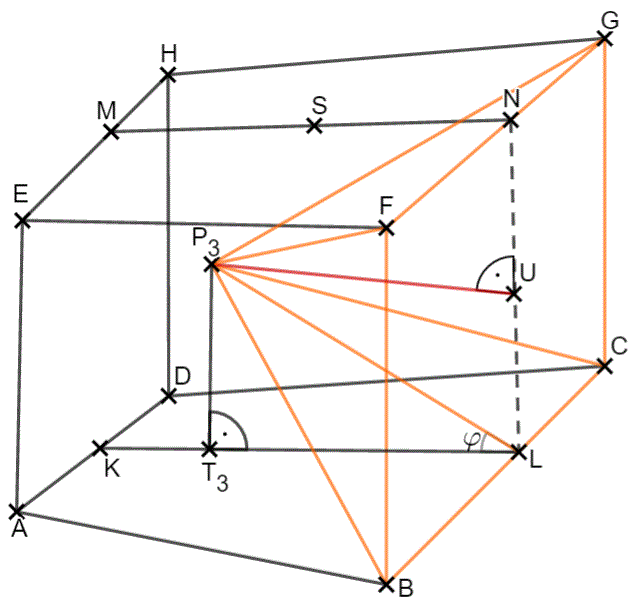
Die Punkte sind die Spitzen von Pyramiden mit den Höhen und auf der Strecke . Zeichnen Sie die Pyramide und ihre Höhe in das Schrägbild zur Teilaufgabe (a) ein.
Zeigen Sie sodann rechnerisch, dass für das Volumen der Pyramiden in Abhängigkeit von gilt: cm³.
Die Pyramide mit der rechteckigen Grundfläche und der Spitze hat dasselbe Volumen wie die Pyramide .
Berechnen Sie den zugehörigen Wert für .