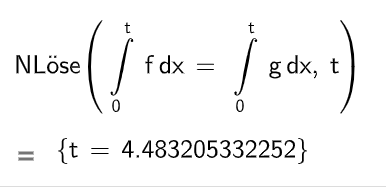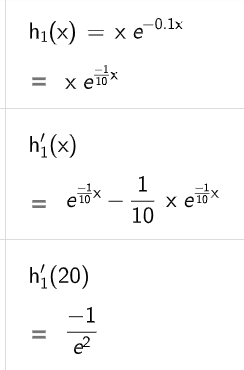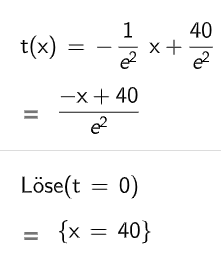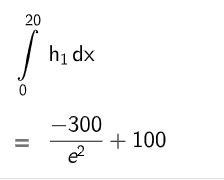Aufgabe 1A
Ein Unternehmen verkauft Fitnessarmbänder.
Die momentane Änderungsrate des Absatzes wird beschrieben mit der in definierten Funktion mit:
Dabei ist die seit der Produkteinführung vergangene Zeit in Monaten und die momentane Änderungsrate des Absatzes in Stück pro Monat.
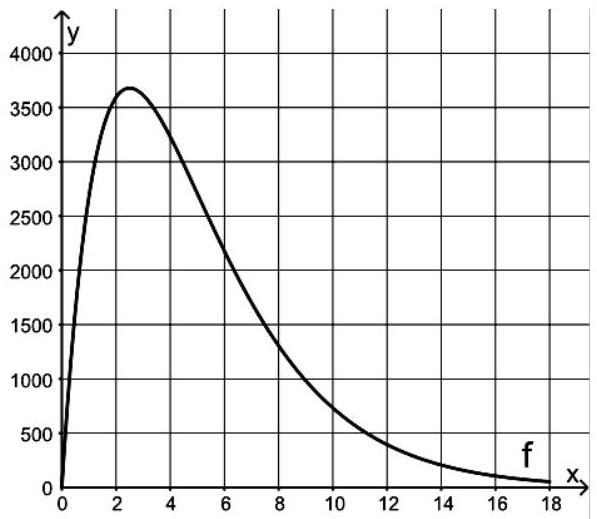
Berechnen Sie den Zeitpunkt, zu dem die momentane Änderungsrate des Absatzes den größten Wert erreicht, und geben Sie diesen größten Wert an.
Kennzeichnen Sie in der Abbildung diejenigen Punkte des Graphen, die zu einer momentanen Änderungsrate des Absatzes in Höhe von 1000 Stück pro Monat gehören. (6BE)
Im Beobachtungszeitraum gibt es einen Zeitpunkt, zu dem die momentane Änderungsrate des Absatzes am stärksten zunimmt, und einen Zeitpunkt, zu dem sie am stärksten abnimmt. Zur Bestimmung dieser beiden Zeitpunkte wurden folgende Berechnungen durchgeführt:
i.
ii.
Erläutern Sie diese beiden Berechnungen.
Bestimmen Sie ohne weitere Rechnung die beiden gesuchten Zeitpunkte. (6BE)
Gleichzeitig mit der Einführung des Fitnessarmbands brachte das Unternehmen eine Smartwatch auf den Markt. Die momentane Änderungsrate des Absatzes der Smartwatch in Stück pro Monat wird mithilfe der in definierten Funktion mit beschrieben. Dabei ist die seit der Produkteinführung vergangene Zeit in Monaten und die momentane Änderungsrate des Absatzes in Stück pro Monat.
Vergleichen Sie die momentanen Änderungsraten des Absatzes für das Fitnessarmband und die Smartwatch fünf Monate nach Produkteinführung. (2BE)
Berechnen Sie die Anzahl der im ersten Jahr nach Produkteinführung insgesamt verkauften Smartwatches.
Untersuchen Sie, ob es einen Zeitpunkt nach Produkteinführung gibt, bis zu dem ebenso viele Fitnessarmbänder wie Smartwatches verkauft wurden.
Geben Sie gegebenenfalls diesen Zeitpunkt an. (6BE)
Gegeben sind nun die in definierten Funktionen mit .
Für jeden Wert von ist der Extrempunkt und der
Wendepunkt des Graphen von .
Betrachtet wird zunächst .
Die nebenstehende Abbildung zeigt den Graphen von .
Geben Sie für den Graphen von die Koordinaten des Extrempunktes und des Wendepunktes an. (2BE)
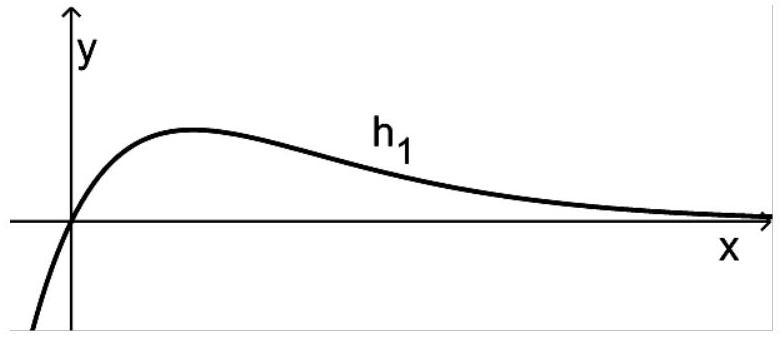
Die Tangente an den Graphen von in dessen Wendepunkt und der Graph von schließen mit der -Achse eine Fläche ein.
Bestimmen Sie deren Flächeninhalt. (6BE)
Jeder Punkt liegt auf einer Ursprungsgeraden und jeder Punkt liegt auf einer anderen Ursprungsgeraden.
Geben Sie die Gleichungen dieser beiden Ursprungsgeraden an. (3BE)
bezeichnet den Koordinatenursprung.
Beurteilen Sie die Gültigkeit der folgenden Aussage: (4BE)
Alle Dreiecke sind ähnlich.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?