Aufgaben zur Volumenberechnung
Mit diesen Aufgaben kannst du üben, das Volumen von Körpern in einem Koordinatensystem zu berechnen.
- 1
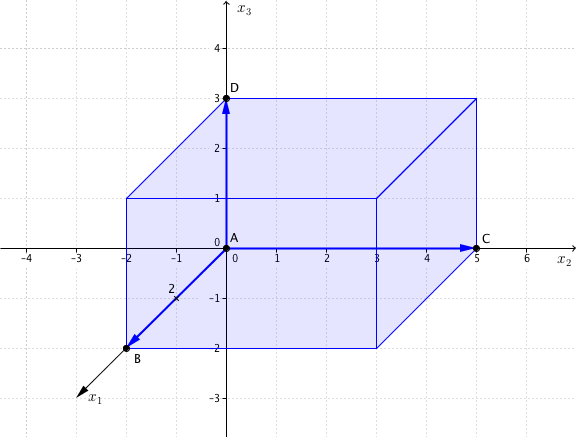
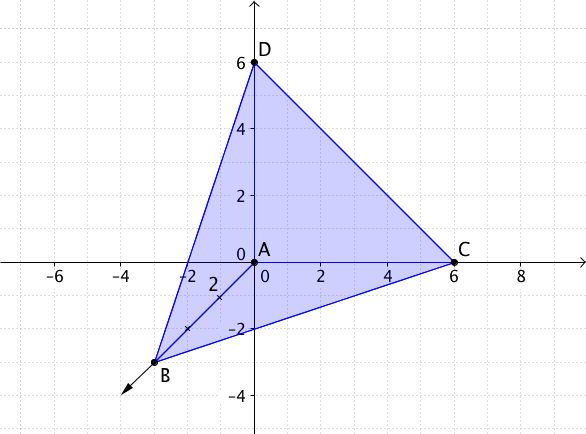
Berechne das Volumen des Parallelotops, das
durch die Punkte , , , aufgespannt wird.
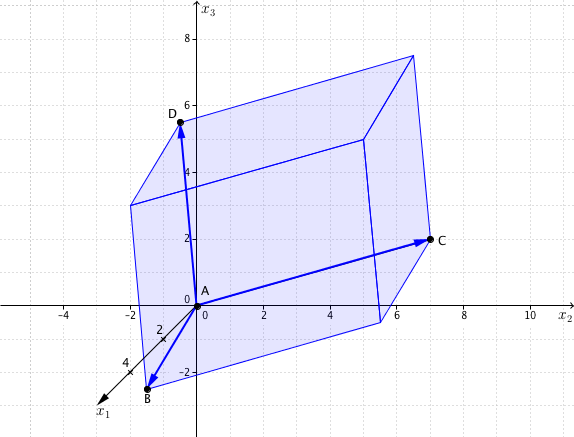
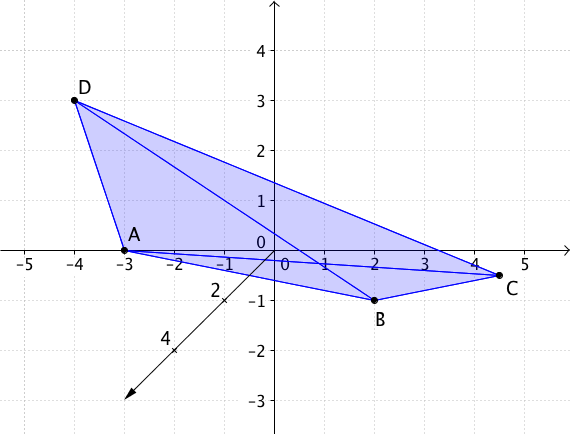
durch die Punkte , , , aufgespannt wird.
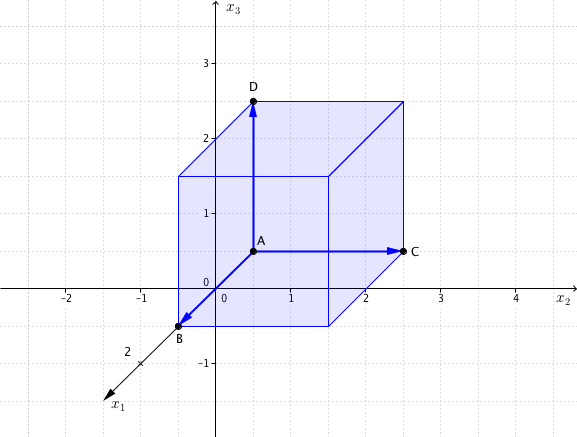
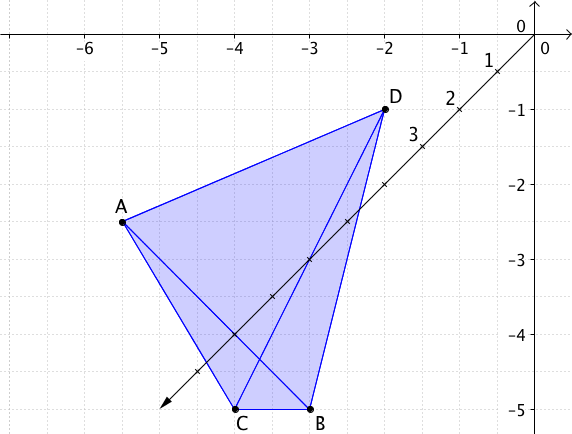
durch die Punkte , , , aufgespannt wird.
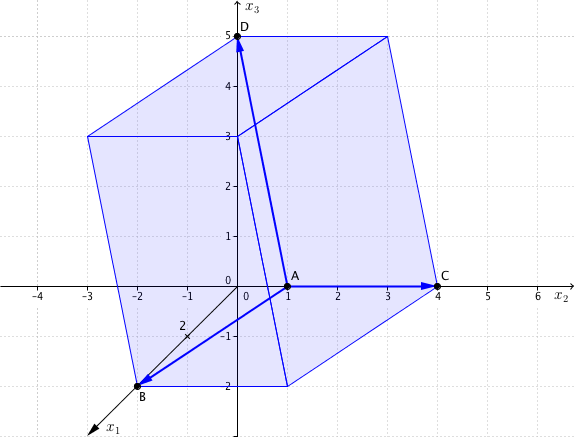
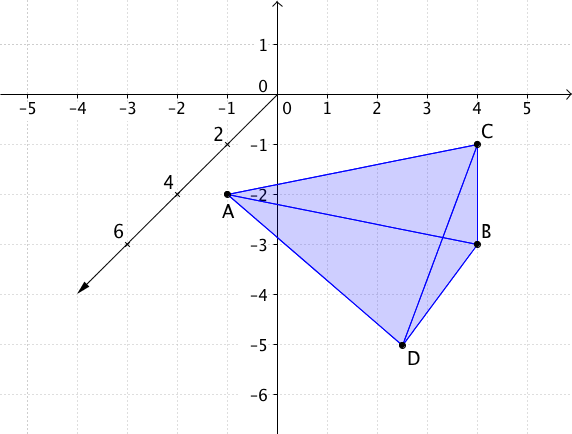
durch die Punkte , , , aufgespannt wird.
durch die Punkte , , , aufgespannt wird.
- 2
Berechne das Volumen des Tetraeders, das
durch die Eckpunkte , , , gegeben ist.
durch die Eckpunkte , , , gegeben ist.
durch die Eckpunkte , , , gegeben ist.
durch die Eckpunkte , , , gegeben ist.
- 3
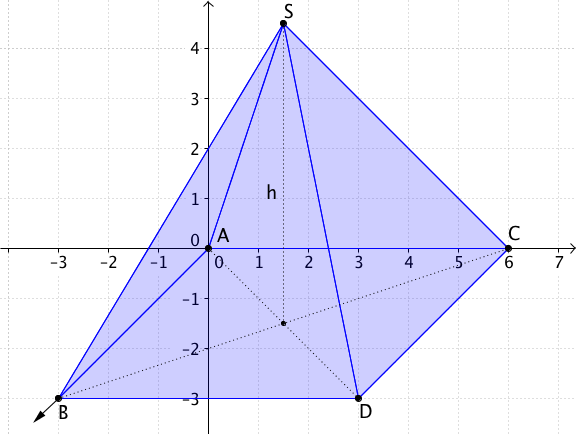
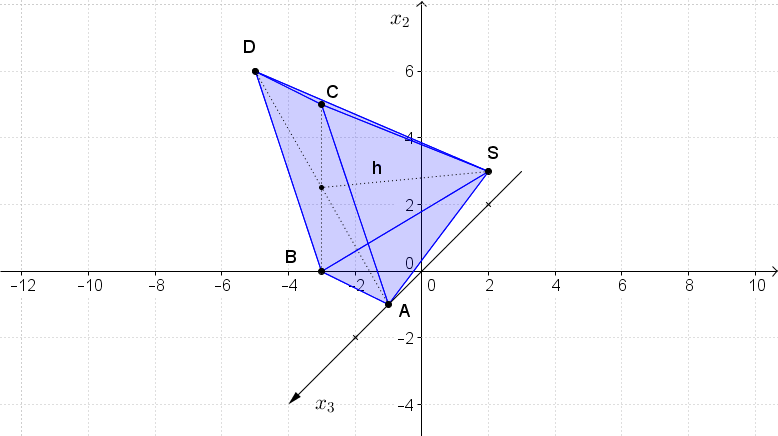
Berechne das Volumen der Pyramide, die
durch die Eckpunkte , , , und die Spitze gegeben ist.
durch die Eckpunkte , , , und die Spitze gegeben ist.
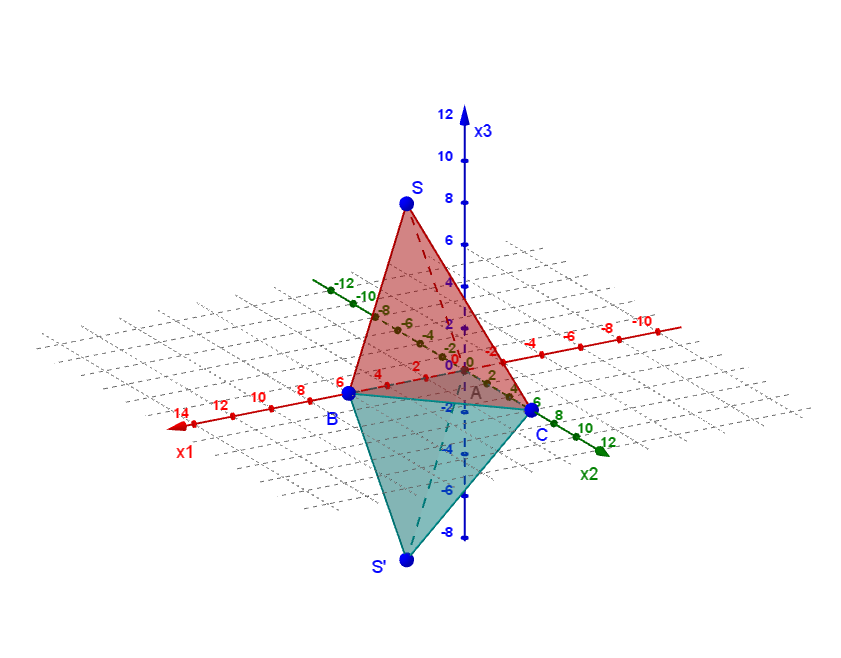
- 4
Ein Tetraeder hat eine Grundfläche, die durch die Eckpunkte , und festgelegt ist. Die Spitze liegt mittig über .
Bestimme mögliche Koordinaten von so, dass das Volumen des Tetraeders genau Volumeneinheiten () beträgt.
Welcher weitere Punkt erfüllt die Vorgabe, dass der Tetraeder ein Volumen von hat und als Höhenfußpunkt besitzt?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?