Gerade an Ebene spiegeln

Geometrische Objekte können an Punkten, Geraden und Ebenen gespiegelt werden.

Eine Gerade $g$ wird an einer Ebene $E$ gespiegelt, indem zwei Punkte der Gerade gespiegelt werden. Diese neuen Punkten legen die Gerade $g^{'}$ eindeutig fest.

Falls ein Schnittpunkt von $g$ und $E$ bekannt ist, kann dieser zum Aufstellen der neuen Gerade verwendet werden, da er unter der Spiegelung gleich bleibt.

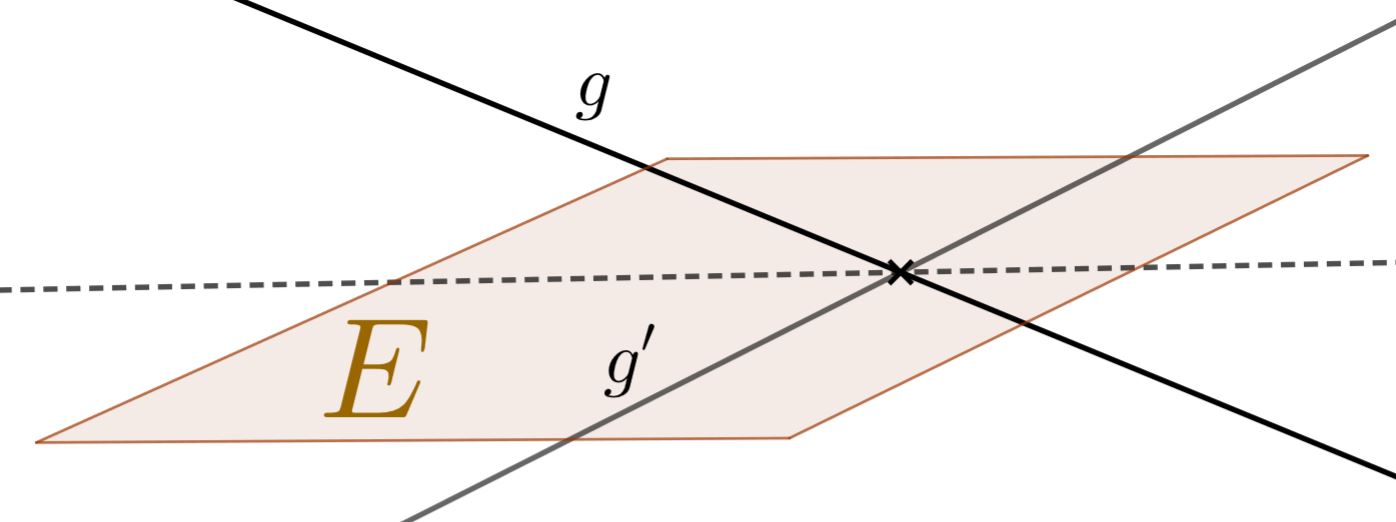
Erklärung am Beispiel

Eine Ebene sei durch die Koordinatenform

E : 2 x_{1} ​ + x_{2} ​ + 2 x_{3} ​ = 20

gegeben. Die zu spiegelnde Gerade lautet:

g : \vec{x} = (\begin{array}{c} 1 \\ - 2 \\ 0 \end{array}) + λ \cdot (\begin{array}{c} 0 \\ 1 \\ - 1 \end{array})

Punkte auf der Gerade bestimmen

Die zwei Punkte, die zur Spiegelung benötigt werden, können fast direkt aus der Gerade entnommen werden. Aus dem Stützvektor $\vec{A}$ folgt, dass der Punkt $A$ in der Gerade $g$ enthalten ist:

\vec{A} = (\begin{array}{c} 1 \\ - 2 \\ 0 \end{array}) \Rightarrow A (1 | - 2 | 0) \in g

Für den Wert $λ = 1$ ergibt sich der zweite Vektor bzw. Punkt $B$ :

\vec{B} = (\begin{array}{c} 1 \\ - 2 \\ 0 \end{array}) + (\begin{array}{c} 0 \\ 1 \\ - 1 \end{array}) = (\begin{array}{c} 1 \\ - 1 \\ - 1 \end{array}) \Rightarrow B (1 | - 1 | - 1) \in g

Hilfsgeraden aufstellen

Die Punkte $A, B$ werden jeweils an der Ebene gespiegelt, indem Hilfsgeraden $h_{1}$ , $h_{2}$ senkrecht auf die Ebene gestellt werden, welche durch die Punkte verlaufen.

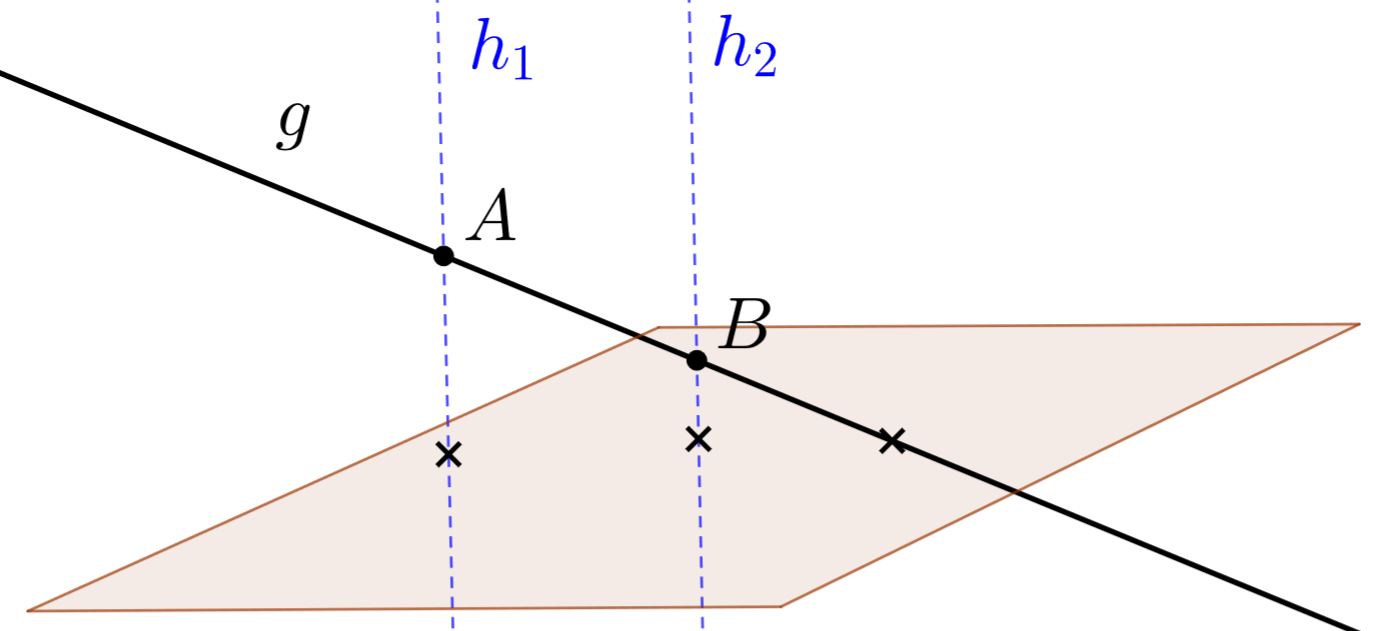
Da die Ebene in Koordinatenform vorliegt, kann der Normalenvektor $\vec{n}$ angegeben werden als:

\vec{n} = (\begin{array}{c} 2 \\ 1 \\ 2 \end{array})

Dieser bildet jeweils den Richtungsvektor dieser senkrechten Hilfsgeraden. Mit den Aufpunkten $A, B$ ergeben sich beide Hilfsgeraden:

h_{1} : \vec{x} = (\begin{array}{c} 1 \\ - 2 \\ 0 \end{array}) + μ_{1} \cdot (\begin{array}{c} 2 \\ 1 \\ 2 \end{array}) h_{2} : \vec{x} = (\begin{array}{c} 1 \\ - 1 \\ - 1 \end{array}) + μ_{2} \cdot (\begin{array}{c} 2 \\ 1 \\ 2 \end{array})

Punkte $A, B$ spiegeln

Die Punkte $A, B$ werden an der Ebene gespiegelt, mithilfe der Hilfsgeraden und den Schnittpunkten $S_{1}, S_{2}$ mit der Ebene. Die Vorgehensweise hierzu ist im Link zu finden.

Für das Beispiel ergeben sich die gespiegelten Punkte $A^{'} (\frac{89}{9} | \frac{22}{9} | \frac{80}{9})$ , $B^{'} (\frac{95}{9}, \frac{41}{9}, \frac{73}{9})$ .

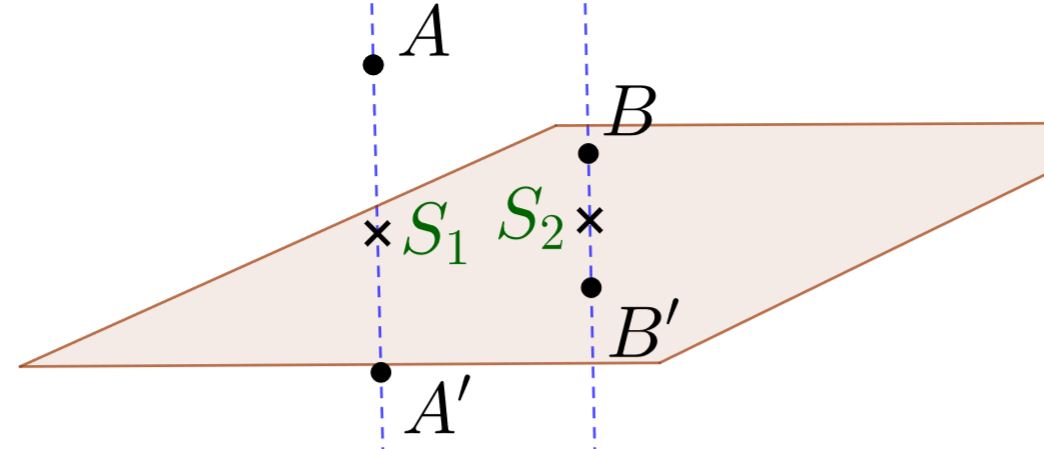
Gespiegelte Gerade $g^{'}$ aufstellen

Die gespiegelten Punkte $A^{'}, B^{'}$ legen die gespiegelte Gerade $g^{'}$ eindeutig fest. Diese wird aufgestellt:

$g^{'} : \vec{x}$	$=$	$\vec{O A^{'}} + μ_{3} \cdot \vec{A^{'} B^{'}}$
	↓	Einsetzen
	$=$	$(\begin{array}{c} \frac{89}{9} \\ \frac{22}{9} \\ \frac{80}{9} \end{array}) + μ_{3} \cdot (\begin{array}{c} \frac{95}{9} - \frac{89}{9} \\ \frac{41}{9} - \frac{22}{9} \\ \frac{73}{9} - \frac{80}{9} \end{array})$
	↓	Zusammenfassen
	$=$	$(\begin{array}{c} \frac{89}{9} \\ \frac{22}{9} \\ \frac{80}{9} \end{array}) + μ_{3} \cdot (\begin{array}{c} \frac{2}{3} \\ \frac{19}{9} \\ - \frac{7}{9} \end{array})$

Die Gerade ist damit:

g^{'} : \vec{x} = (\begin{array}{c} \frac{89}{9} \\ \frac{22}{9} \\ \frac{80}{9} \end{array}) + μ_{3} \cdot (\begin{array}{c} \frac{2}{3} \\ \frac{19}{9} \\ - \frac{7}{9} \end{array})

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?