Additionsverfahren

Das Additionsverfahren ist eine Methode zum Lösen von linearen Gleichungssystemen.

Das Ziel ist, dass eine Variable wegfällt, wenn man die Gleichungen addiert oder subtrahiert. Man kann das Verfahren also anwenden, wenn in beiden Gleichungen der gleiche Term vorkommt.

Lineares Gleichungssystem mit zwei Gleichungen und zwei Variablen

Beispiel

Gegeben ist das lineare Gleichungssystem:

$(I) 3 x$	$=$	$2 y$
$(I I) 10 - 3 x$	$=$	$y + 1$

Eine genauere Einführung des Beispiels findest du unter lineares Gleichungssystem.

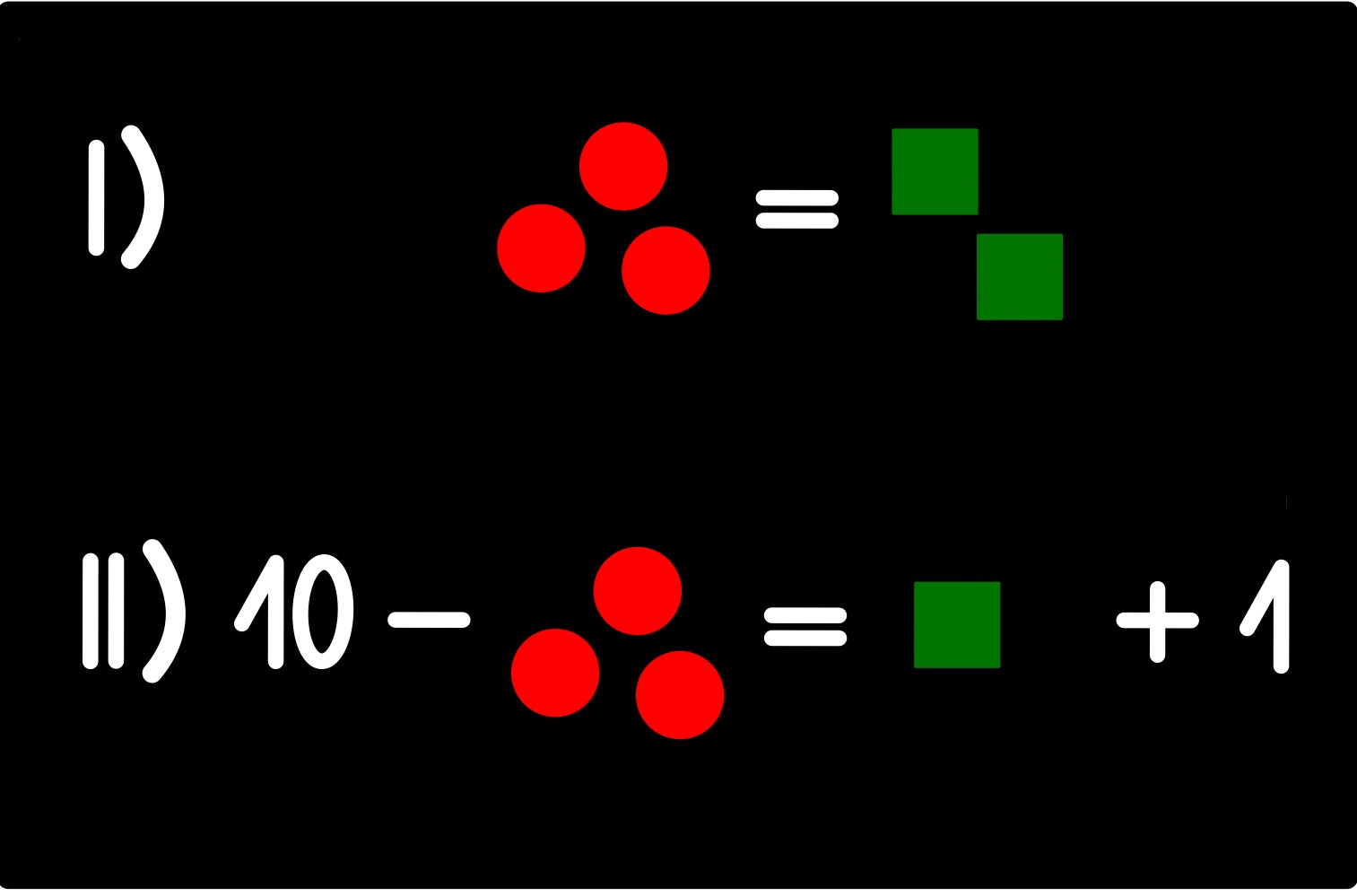
Hier kommt in beiden Gleichungen 3x vor. Weil in (I) +3x und in (II) -3x steht, können wir einfach I + II rechnen:

$3 x$	$=$	$2 y$
$+ 10 - 3 x$	$=$	$y + 1$
	↓	Durch Addition fällt x weg.
$10$	$=$	$3 y + 1$

Jetzt haben wir nur noch eine Gleichung mit einer Unbekannten (y). Diese lösen wir jetzt nach y auf.

$10$	$=$	$3 y + 1$	$- 1$
$9$	$=$	$3 y$	$: 3$
$3$	$=$	$y$
	↓	Wir bekommen also für y raus:
$y$	$=$	$3$

Jetzt können wir y = 3 in eine der beiden Gleichungen (I oder II) einsetzen, um x rauszubekommen. Gleichung (I) ist kürzer, deswegen geht es schneller, wenn wir y = 3 in (I) einsetzen:

$3 x$	$=$	$2 \cdot 3$
$3 x$	$=$	$6$	$: 3$
	↓	Wir bekommen also für x raus:
$x$	$=$	$2$

Die Lösung ist also: x = 2 und y = 3.

Man kann das Ergebnis auch als Lösungsmenge schreiben: $L = {(2; 3)}$ .

Wie oben bereits erklärt, wendet man das Additionsverfahren an, wenn in beiden Gleichungen der gleiche Term vorkommt. Man kann aber auch eine Gleichung mit einer Zahl multiplizieren, um einen gleichen Term zu erhalten.

Lineares Gleichungssystem mit drei Gleichungen und drei Variablen

Beispiel

Gegeben ist das lineare Gleichungssystem:

$(I) - 4 x - 6 y + 2 z$	$=$	$- 22$
$(I I) x - y + 2 z$	$=$	$3$
$(I I I) 3 x - 2 y + 3 z$	$=$	$8$

In Gleichung (I) und Gleichung (II) taucht jeweils der Term 2x auf. Wir können also Gleichung (I) und (II) subtrahieren:

(I) - (II):
	↓
$- 4 x - 6 y + 2 z$	$=$	$- 22$
$- (x - y + 2 z)$	$=$	$3$

Notation	Erläuterung
$\begin{array}{rccccc} I & 2 a & + & 3 b & - & c & = & 11 \\ II & a & - & b & + & 2 c & = & 3 \\ III & 3 a & - & 2 b & + & 3 c & = & 8 \end{array}$	Wie oben wählt man eine Variable aus und findet das kleinste gemeinsame Vielfache der Koeffizienten. Hier wählt man $a$ und berechnet: $k g V (1; 2; 3) = 6$ Nun vervielfacht man die Gleichungen so, dass die Koeffizienten der Variable in allen Gleichungen gleich dem [kgV]() sind. Hier: Man multipliziert die erste Gleichung mit $3$ , die zweite mit $6$ , die dritte mit $2$ .
$\begin{array}{rccccc} 3 \cdot I \to I^{'} & 6 a & + & 9 b & - & 3 c & = & 33 \\ 6 \cdot I I \to I I^{'} & 6 a & - & 6 b & + & 12 c & = & 18 \\ 2 \cdot I I I \to I I I^{'} & 6 a & - & 4 b & + & 6 c & = & 16 \end{array}$	Nun addiert (oder subtrahiert) man die Gleichungen voneinander, um die gewählte Variable zu eliminieren. Hier: Man subtrahiert $I^{'}$ von ${II}^{'}$ und von ${III}^{'}$ .
$\begin{array}{rccccc} I^{'} & 6 a & + & 9 b & - & 3 c & = & 33 \\ I I^{'} - I^{'} \to I I^{''} & 6 a - 6 a & - & 6 b - 9 b & + & 12 c - (- 3 c) & = & 18 - 33 \\ I I I^{'} - I^{'} \to I I I^{''} & 6 a - 6 a & - & 4 b - 9 b & + & 6 c - (- 3 c) & = & 16 - 33 \end{array}$ $\begin{array}{rccccc} I^{'} & 6 a & + & 9 b & - & 3 c & = & 33 \\ I I^{'} - I^{'} \to I I^{''} & 6 a - 6 a & - & 6 b - 9 b & + & 12 c - (- 3 c) & = & 18 - 33 \\ I I I^{'} - I^{'} \to I I I^{''} & 6 a - 6 a & - & 4 b - 9 b & + & 6 c - (- 3 c) & = & 16 - 33 \end{array}$	Nun bilden ${II}^{''}$ und ${III}^{''}$ ein Gleichungssystem mit zwei Unbekannten. Man löst dieses neue Gleichungssystem wie oben beschrieben und erhält: $b = 2; c = 1$ . Diese beiden Werte setzt man dann in $I^{'}$ ein und löst nach $a$ auf.
$\begin{array}{rrcl} b und c in I^{'} \to I^{''} & 6 a + 9 \cdot 2 - 3 \cdot 1 & = & 33 \\ 6 a + 15 & = & 33 & \| - 15 \\ 6 a & = & 18 & \| : 6 \\ a & = & 3 \end{array}$	Insgesamt erhält man $a = 3, b = 2$ und $c = 1$ . Die Werte für $a$ und $b$ schreibt man in ein Tupel. Die Lösungsmenge lautet: $L = {(3; 2; 1)}$

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Videos

Additionsverfahren

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?