Normale

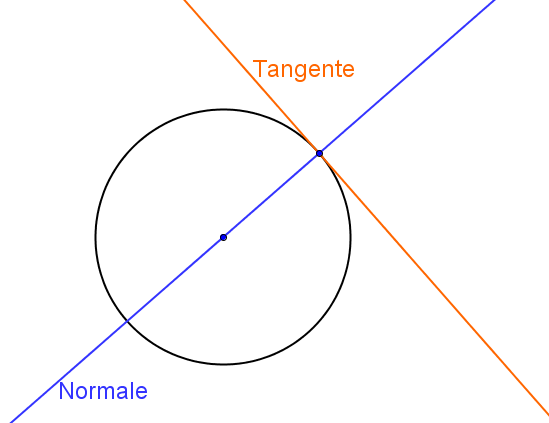
Normalenformel

Die Normale $g$ ist damit gegeben durch eine lineare Funktion und kann mithilfe der Normalenformel aufgestellt werden:

Bestimmen der Normalensteigung $m_n$

Ausgehend von einer Tangente (oder allgemein einer Geraden) ist es zu deren Normalen nicht weit. Da diese beiden Geraden senkrecht aufeinander stehen, erfüllen ihre Steigungen $m_t$ und $m_n$ folgende Gleichung:

und damit lässt sich $m_n$ berechnen mithilfe:

Beispiele zur Bestimmung von $m_n$

Normalengleichung aufstellen

Setzt man die Steigung $m_n$ in die allgemeine Geradengleichung ein, besitzt die Normale die Form:

Hier steht $b$ für den y-Achsenabschnitt der Normale. Diesen können wir berechnen, indem für $x$ und $g\left(x\right)$ die Koordinaten eines Punktes $P\left(x|y\right)$ eingesetzt werden.

Beispiel zur Berechnung des y-Achsenabschnittes $b$

Eine Normale habe die Steigung $m_n=-2$ und verlaufe durch den Punkt $P(-3|-4)$. Wir berechnen deren y-Achsenabschnitt. Dieser Ablauf ist für die Berechnung des y-Achsenabschnittes immer gleich und lässt sich ganz allgemein anwenden.

Die Normale wird durch den Funktionsterm $g(x)=-2x-10$ beschrieben.

Normalenformel

Das Aufstellen der Normalengleichung ist genauso systematisch wie das Bestimmen einer Tangente und kann mit der Formel

vorgenommen werden.