Das Oktalsystem wird in der heutigen Zeit in erster Linie in der Digitaltechnik eingesetzt. Neben der Nutzung zur Darstellung der klassischen Unix Dateisystem Zugriffsrechte findet es aber auch noch in der Flugsicherung ein Anwendungsgebiet. Der Transponder-Code, dient im Luftverkehr zur eindeutigen Identifizierung eines Luftfahrzeugs und wird vom Piloten durch eine vierstellige Oktalzahl bestimmt. [1].
Definition
Das Oktalsystem (von lateinisch octo ‚acht‘) ist ein Stellenwertsystem auf Basis 8 (daher auch Achtersystem genannt). Es kennt acht Ziffern zur Darstellung einer Zahl: 0, 1, 2, 3, 4, 5, 6 und 7. [2] Die Ziffern haben den gleichen Wert wie im Dezimalsystem.
Wobei R für die Basis (hier 8) und Z für die Menge seiner Ziffern steht.
Das Oktalsystem ist ebenso wie auch das Binärsystem eines der grundlegenden Zahlensysteme im Zusammenhang mit der Nutzung von Computern. Es zeichnet sich durch eine deutlich kompaktere Darstellung der Zahlen (im Vergleich zum Binärsystem) aus.
Vorteile des Oktalsystems
Darstellung der Zahlen braucht nur ein Drittel der binären Länge
Einfacher Konvertierungsprozess von Binär- nach Oktal-Zahlen und umgekehrt
Nachteile des Oktalsystems
Zusätzlicher Oktal-Binär-Wandler erforderlich, da Computer nur binäre Zahlen verarbeiten können
Darstellung
Zur Darstellung einer Zahl im Oktalsystem werden die Ziffern wie auch im Dezimalsystem ohne Trennzeichen hintereinander geschrieben. Ihr Stellenwert entspricht der zur Stelle passenden Achterpotenz. Die höchstwertige Stelle wird ganz links und die niederwertigeren Stellen in absteigender Reihenfolge rechts davon aufgeschrieben.
Die Stellenzählung beginnt mit 0.
Jede Ziffer einer Oktalzahl kann durch drei Stellen einer Binärzahl dargestellt werden. Umgekehrt kann aus einer Binärzahl durch Gruppierung von jeweils drei Bit leicht eine Oktalzahl erzeugt werden.
Oktal |
|
|
|---|---|---|
Binär |
| |
Dezimal |
|
Wenn man im Dezimalsystem zählt, erhöht man nach 10 Ziffern die Stelligkeit um 1 und die nächste Ziffer ist eine 0. So folgt z.B. nach der 9 die 10 oder nach der 99 die 100.
Im Oktalsystem funktioniert es genauso. Nach der 7 kommt eine 10 bzw. nach der 77 die 100.
Dezimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
Oktal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 |
Umrechnung in andere Stellenwert-Systeme
Um eine Oktalzahl in eine Dezimalzahl umzurechnen, muss man die einzelnen Ziffern mit der Potenz des Stellenwertes zur Basis (hier 8) ermitteln. Somit ergeben sich folgende Dezimalzahlen zu den Stellennummern 0 bis 4.
| |
|---|---|
|
|
|
|
|
|
|
|
|
|
Beispiel: Umrechnung der Oktalzahl: 126 in Dezimal
Oktalzahl: | 1 | 2 | 6 |
|---|---|---|---|
Stellennummer: | 2 | 1 | 0 |
Stellenwert: |
|
|
|
Potenzwert: |
|
|
|
Addiert man nun die einzelnen Potenzwerte der Stellen, bekommt man den Gesamtwert der Oktalzahl: als Dezimalzahl:
Anwendungen
Eine der wichtigsten Anwendung der Oktalzahlen ist die Darstellung der Zugriffsrechte in Unix Dateisystemen. Dabei werden die Rechte der drei Gruppen:
Benutzer (user)
Gruppe (group)
Alle andren (others)
jeweils durch eine Oktalzahl beschrieben. Die drei Buchstaben [r, w, x] innerhalb der Gruppe werden wie folgt dargestellt.
Ausdruck | Translate | Zahl |
|---|---|---|
|
| |
|
| |
|
|
Ein Benutzer (user), der Lese-, Schreib- und Ausführungsrechte auf eine Datei hat und die Mitglieder der beiden andren Gruppen (group, others) keinerlei Rechte würde dementsprechend wie folgt beschrieben:
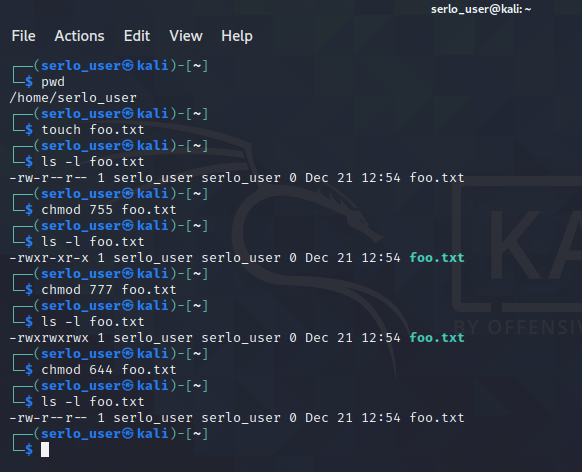
Beispiele weiterer Zugriffsrechte in Unix Dateisystemen:
Befehl | Users | Group | Others |
|---|---|---|---|
$ chmod 644 |
|
|
|
$ chmod 755 |
|
|
|
$ chmod 777 |
|
|
|
Aufgaben
Übungsaufgaben
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
- Zahlensysteme
- Stellenwertsysteme
- Dezimalsystem
- Binärsystem
- Additionssysteme
- Hybridsysteme
- Hexadezimalsystem
- Römische Zahlen
