Über Kreuz multiplizieren

Man verwendet dieses Verfahren bei Brüchen oder Bruchtermen in Gleichungen. Dabei ist das Ziel der Methode, dass die Nenner wegfallen und man somit keine Brüche bzw. Bruchterme mehr hat.

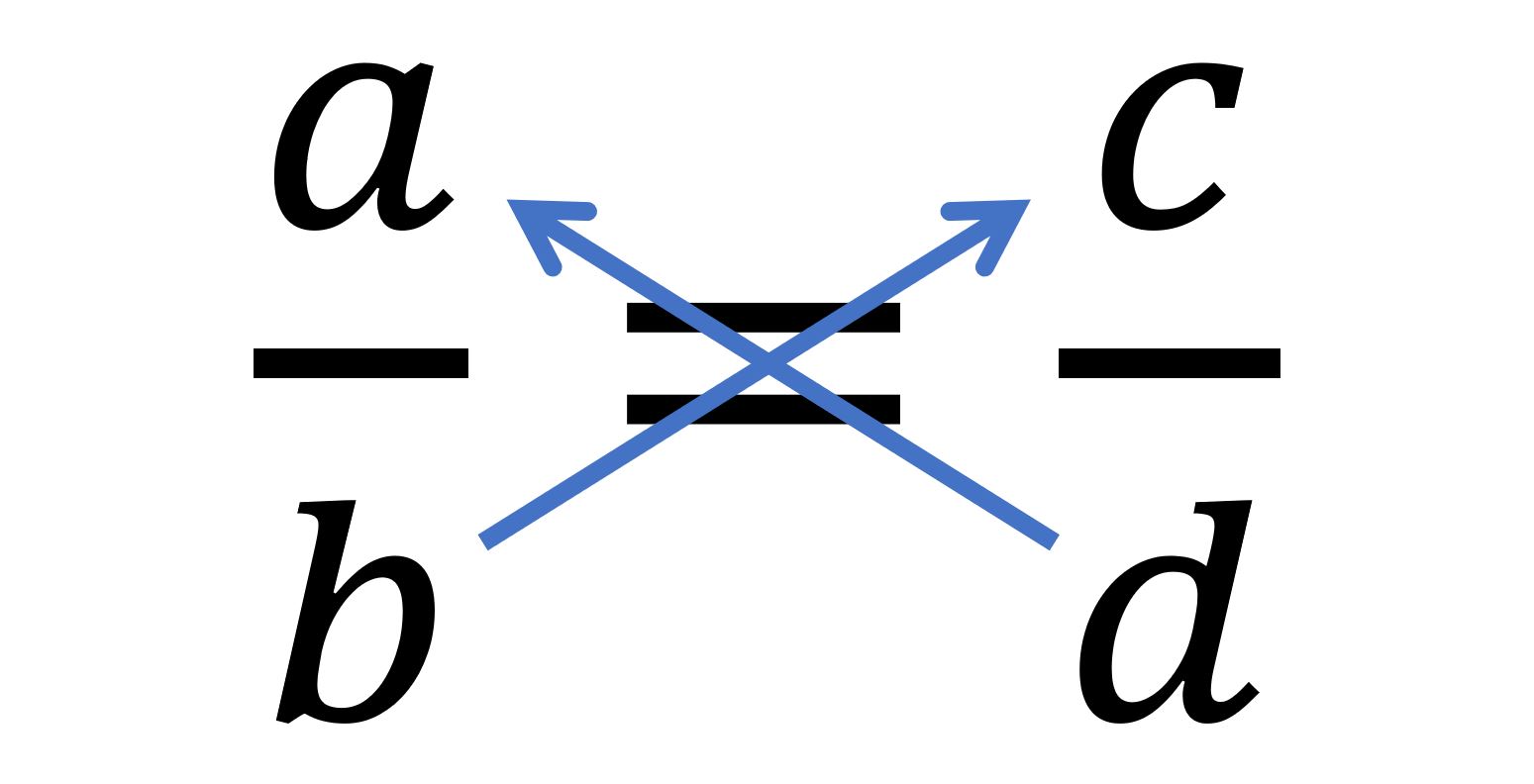
Vorgehen

Beim "Über Kreuz multiplizieren" wird der Nenner von einer Seite auf die andere Seite der Gleichung multipliziert und andersrum.

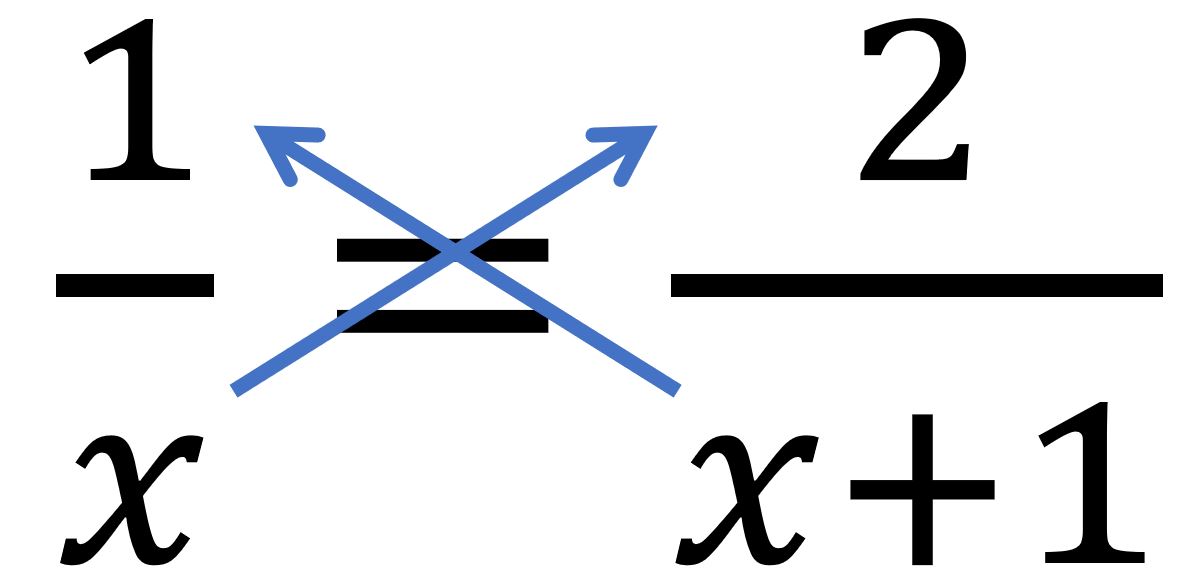
Gegeben: $\frac{1}{x} = \frac{2}{x + 1}$

$\frac{1}{x}$	$=$	$\frac{2}{x + 1}$	$\cdot x$
$\frac{1 \cdot x}{x}$	$=$	$\frac{2 \cdot x}{x + 1}$
	↓	Kürze auf der linken Seite der Gleichung
$1$	$=$	$\frac{2 \cdot x}{x + 1}$	$\cdot (x + 1)$
$1 \cdot (x + 1)$	$=$	$\frac{2 \cdot x \cdot (x + 1)}{x + 1}$
	↓	Kürze
$(x + 1)$	$=$	$2 \cdot x$

Weitere Übungungsaufgaben: Über Kreuz multiplizieren

Voraussetzung

Achtung! Bevor dieses Verfahren angewendet werden kann, muss man sicherstellen, dass im Fall einer Summe bzw. Differenz auf einer Seite der Gleichung diese Brüche auf einen Nenner gebracht werden.

Veranschaulichung am Applet

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/htENv4rC]

Übungsaufgaben

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Methode des Über-Kreuz-Multiplizierens

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?