Stochastik, Teil B, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Ein Unternehmen stellt Kunststoffteile her. Erfahrungsgemäß sind 4% der hergestellten Teile fehlerhaft. Die Anzahl fehlerhafter Teile unter zufällig ausgewählten kann als binomialverteilt angenommen werden.
a)
(3 BE)
50 Kunststoffteile werden zufällig ausgewählt. Bestimmen Sie für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:
A: "Genau zwei der Teile sind fehlerhaft."
B: "Mindestens 6% der Teile sind fehlerhaft."
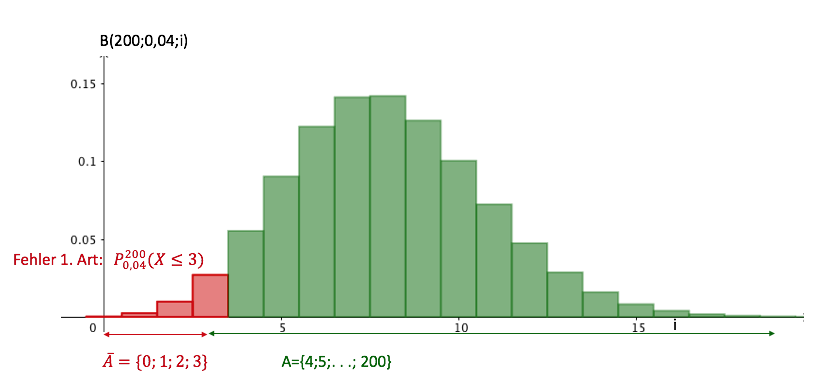
Die Kunststoffteile werden aus Kunststoffgranulat hergestellt. Nach einem Wechsel des Granulats vermutet der Produktionsleiter, dass sich der Anteil der fehlerhaften Teile reduziert hat. Um einen Anhaltspunkt dafür zu gewinnen, ob die Vermutung gerechtfertigt ist, soll die Nullhypothese "Der Anteil der fehlerhaften Teile beträgt mindestens 4%" auf der Grundlage einer Stichprobe von 200 Teilen auf einem Signifikanzniveau von 5% getestet werden.
b)
(4 BE)
Bestimmen Sie die zugehörige Entscheidungsregel.
c)
(3 BE)
Das neue Granulat ist teurer als das vorherige. Geben Sie an, welche Überlegung zur Wahl der Nullhypothese geführt haben könnte, und begründen Sie Ihre Angabe.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Lösung Teilaufgabe a)
$X$ sei die Zufallsgröße, welche die Anzahl fehlerhafter Kunststoffteile beschreibt.
$n=50$ und $p=0{,}04$
$X$ ist $B(50;0{,}04)$ verteilt
$\color{red}{\text{Beachte}:}$ $4{\%}$ = $\frac{4}{100}=0{,}04$ und nicht $0{,}4$ !
Benutze das Tafelwerk zur Stochastik.
Ereignis $A$ : "Genau zwei Teile sind fehlerhaft".
$P(A)=P_{0{,}04}^{50}(X=2)\overset{\text{Tafel}}{=}0{,}27623\approx{27{,}6\,}{\%}$
Die Wahrscheinlichkeit für das Ereignis $A$ beträgt rund $27{,}6{\%}.$
Ereignis $B$ : "Mindestens 6% der Teile sind fehlerhaft".
Die Mächtigkeit für das Ereignis $B$ beträgt:
$|B|=6{\%}\; von \;50 = 3$ .
"Mindestens drei Teile schadhaft" heißt: $"X\geq3"$
$\def\arraystretch{1.25} \begin{array}{rcll}\quad P(\mathrm{B})&=&P_{0{,}04}^{50}\left(\mathrm{X}\geq3\right)&|\;\color{red}{\text{Gegenereignis}}\;\text{heranziehen}!\\&=&\color{red}{1-}\,P_{0{,}04}^{50}(\mathrm{X}\color{red}{\leq{2}})&|\;\text{Tafel benutzen}\\&=&1-0{,}67671\\&=&0{,}32329\\&\approx& 32{,}3\,{\%}\end{array}$
Das Ereignis $\mathrm{B}$ hat die Wahrscheinlichkeit von rund $32{,}3\,{\%}$ .
Lösung Teilaufgabe b)
Arbeitsplan zur Durchführung des notwendigen Signifikanztestes für die Bestimmung einer Entscheidungsregel durch Angabe des Annahme- und Ablehnungsbereichs:
Die vorgegebene Nullhypothese lautet
$H_0:~$ "Der Anteil fehlerhafter Teile beträgt mindestens 4 %" Es wird vermutet, dass der Anteil fehlerhafter Teil abgenommen hat. Die Gegenhypothese des Produktionsleiters lautet: $H_1:$ . "Der Anteil fehlerhafter Teile hat abgenommen."
Verwendung der binomialverteilten Zufallsgröße $\;X$ , welche die Anzahl fehlerhaften Teile misst, beim Stichprobenumfang $n$ zum vorgegebenen Signifikanzniveau $\alpha$ .
Ansatz für einen linksseitigen Signifikanztest, da für die $H_0$ gilt: " mindestens $4\%$ fehlerhafte Teile" und $H_0$ dann abgelehnt wird, wenn tendenziell wenige Teile in der Stichprobe fehlerhaft sind: Zu erwarten ist dadurch ein Ablehnungsbereich $\;\overline{A}=\{\color{red}{0};1;…;\color{red}{c}\}$ mit der Bestimmung des größtmöglichen Wertes für $c$ mithilfe des Tafelwerks so, dass der Fehler 1. Art das Signifikanzniveau nicht übersteigt. Also wird bei einem $H_0=\{\,p\,|\,p\geq p_0\}$ gefordert: $P_{\color{red}{p_0}}^{n}(X\in\color{red}{\overline{A}})\leq\alpha$ Anmerkung: Du betrachtest nur den "Extremwert" $p_0$ zur Bestimmung des Ablehnungsbereichs $\overline{A}$ . Damit ist gesichert, dass auch für ungünstigere Werte $p$ der Fehler 1. Art das Signifikanzniveau nicht überschreitet.
Angabe der geforderten Entscheidungsregel.
Durchführung des Testes
1.
$H_0=\{p\,|\,p\geq 0{,}04\}$
$H_1=\{p\,|\,p<0{,}04\}$
2.
$n=200$
$\alpha=0{,}05$
3.
Für den Wahrscheinlichkeitswert $p=0{,}04$ suchst du in der kumulativen Verteilungsfunktion der stochastischen Tafel (rechte Spalte!) in der Tabelle für $n=200$ den größten Wert kleiner als $0{,}05$ und liest das dazu gehörende $c$ ab.
$P_{0{,}04}^{200}(X\leq c)=\displaystyle \sum_{i=0}^{200}B(200;0{,}04;i)\;\overset{\text{Tafel}}{\Rightarrow}$
$0{,}03953=\displaystyle\sum_{i=0}^{\color{red}{3}}B(200;0{,}04;i)=P_{0{,}04}^{200}(X\leq \color{red}{3})$
$\Rightarrow\quad c=3\quad\Rightarrow\quad \overline{A}=\{0;1;2;3\}$
4.
Aus dem Ablehnungsbereich $\overline{A}=\{0;1;2;3\}$ folgt beim Stichprobenumfang $200$ der Annahmebereich $A=\{4;…;200\}$ .
Die Entscheidungsregel formulierst du zum Beispiel so:
Die Nullhypothese "Der Anteil fehlerhafter Teile beträgt mindestens $4{\%}$ " wird angenommen, wenn unter den 200 zufällig entnommenen Kunststoffteilen mindestens 4 fehlerhafte Teile sind.
Oder du formulierst so:
Die Nullhypothese ""Der Anteil der fehlerhaften Teile beträgt mindestens $4{\%}$ " wird abgelehnt, wenn unter den 200 zufällig entnommenen Kunststoffteilen höchstens 3 fehlerhafte Teile sind.
Graphische Ergänzung
Den linksseitigen Signifikanztest zur Nullhypothese $H_0=\{\,p\,|\,p\geq0{,}04\}$ beim Signifikanzniveau $\alpha=5\%$ und einem Stichprobenumfang $n=200$ verdeutlicht die nachfolgende Graphik.
Lösung Teilaufgabe c)
In dieser Aufgabe sollst du die Verwendung einer vorgegebenen Nullhypothese im Sachzusammenhang argumentativ begründen.
So könntest du argumentieren:
Der Signifikanztest zur Nullhypothese (der Anteil fehlerhafter Teile beträgt mindestens $4\%$ ) gibt mit seiner Entscheidungsregel - je nach Ausgang des Testes - dem Produktionsleiter eine Information, ob sie abgelehnt werden kann und das neue teuere Granulat damit mit großer Sicherheit die erhoffte positive Wirkung der Verringerung der Zahl der fehlerhaften Teile hat und weiter verwendet werden kann.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
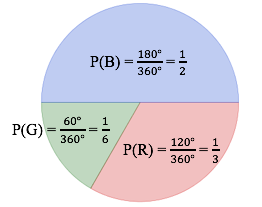
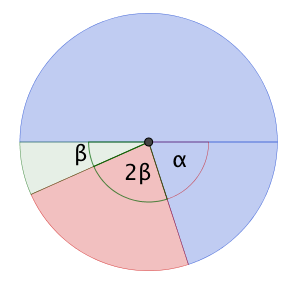
Für ein Spiel wird ein Glücksrad verwendet, das drei farbige Sektoren hat. Der Tabelle können die Farben der Sektoren und die Größen der zugehörigen Mittelpunktswinkel entnommen werden.
Farbe
Blau
Rot
Grün
Mittelpunktswinkel
180°
120°
60°
Für einen Einsatz von 5 Euro darf ein Spieler das Glücksrad dreimal drehen. Erzielt der Spieler dreimal die gleiche Farbe, werden ihm 10 Euro ausgezahlt. Erzielt er drei verschiedene Farben, wird ein anderer Betrag ausgezahlt. In allen anderen Fällen erfolgt keine Auszahlung.
a)
(2 BE)
Die Wahrscheinlichkeit dafür, dass dreimal die gleiche Farbe erzielt wird, ist $\frac1 6$ . Zeigen Sie, dass die Wahrscheinlichkeit dafür, dass drei verschiedene Farben erzielt werden, ebenfalls $\frac1 6$ beträgt.
b)
(3 BE)
Bei dem Spiel ist zu erwarten, dass sich die Einsätze der Spieler und die Auszahlungen auf lange Sicht ausgleichen. Berechnen Sie den Betrag, der ausgezahlt wird, wenn drei verschiedene Farben erscheinen.
c)
(5 BE)
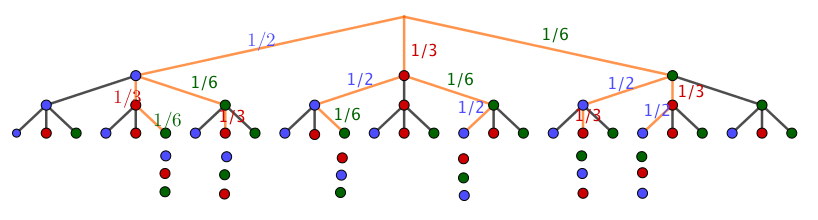
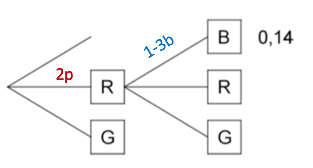
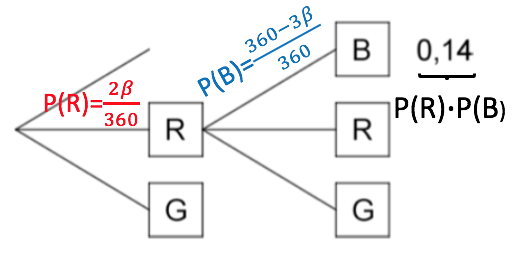
Die Größen der Sektoren werden gändert. Dabei werden der grüne und der rote Sektor verkleinert, wobei der Mittelpunktswinkel des roten Sektors wieder doppelt so groß wie der des grünen Sektors ist. Die Abbildung zeigt einen Teil eines Baumdiagramms, das für das geänderte Glücksrad die beiden ersten Drehungen beschreibt. Ergänzend ist für einen Pfad die zugörige Wahrscheinlichkeit angegeben.
Bestimmen Sie die Größe des zum grünen Sektor gehörenden Mittelpunktswinkel.
Die Aufgaben löst du mit Mitteln der Kombinatorik sowie Kenntnissen über Baumdiagramme und ihren Pfadregeln. Außerdem musst du über den Erwartungswert von Zufallsgrößen Bescheid wissen.
Lösung Teilaufgabe a)
Das dreimalige Drehen eines Glücksrades ist ein mehrstufiges Zufallsexperiment und entspricht im Urnenmodell dem Ziehen mit Zurücklegen. Wahrscheinlichkeitsberechnungen von Ereignissen führst du kombinatorisch oder mit Hilfe von Baumdiagrammen durch.
Das vorliegende Glücksrad lässt sich durch eine Urne mit Kugeln der Farben blau, rot und grün im Zahlenverhältnis $180:120:60=3:2:1$ modellieren.
Kombinatorische Berechnung für $P(\text{"drei verschiedene Farben erzielen"})$
Für eine bestimmte Reihenfolge der drei Farben beim Drehen/Ziehen erhältst du nach der Produktregel der Berechnung der Gesamtwahrscheinlichkeit den Wert $\frac {1}{ 2}\cdot \frac{1}{3}\cdot \frac{1}{6}$ .
Für drei Elemente gibt es kombinatorisch $3!=3\cdot 2 \cdot 1 = 6$ Möglichkeiten der Reihenfolge, so dass sich wegen der Summenregel beim Berechnen von einzelnen Teilwahrscheinlichkeiten die Gesamtwahrscheinlichkeit ergibt:
$P("\text{drei verschiedene Farben erzielen"})=6\cdot \frac{1}{2} \cdot \frac{1}{3} \cdot \frac{1}{6}=\frac{1}{6}$
Lösung über ein Baumdiagramm
Kombinatorische Lösungen mit systematischen Anordnungs- und Auswahlgesichtspunkten (etwa unter Verwendung von Fakultäten und/oder Binomialkoeffizienten) sind bei Berechnungen von Wahrscheinlichkeiten oft elegant und zeitsparend, bergen aber auch die Gefahr in sich, dass du gelegentlich ein Detail der Aufgabenstellung übersiehst oder falsch interpretierst.
Der Einsatz eines Baumdiagramms ist zwar arbeitsintensiver, dafür aber anschaulicher und oft auch "sicherer".
Veranschaulichung des Ereignisses "drei verschiedene Farben" mithilfe eines Baumdiagramms:
Das Ereignis "drei verschiedene Farben" ergibt sich im Baumdiagramm über 6 verschiedene Pfade, so dass gilt:
$\quad\quad\quad P(\text{"drei verschiedene Farben"})=3!\cdot \color{blue}{\frac{1}{2}} \cdot \color{red}{\frac{1}{3}} \cdot \color{green}{\frac{1}{6}}=\frac{1}{6}$
Lösung Teilaufgabe b)
Mit folgenden drei Denk- und Arbeitsschritten bestimmst du für das Glücksspiel eine Zufallsgröße $\,Z :\text{"Auszahlungsbetrag".}$
Die Textangabe zerlegt den Ergebnisraum des Experiments in drei sich ausschließende Ereignisse:
$E_1:\,\text{"drei gleiche Farben"}$ $E_2:\,\text{"drei verschiedene Farben"}$ $E_3:\,\text{"die restlichen Ergebnisse"}$
Der Auszahlungsbetrag ist bei Eintritt von $E_1$ $10.-€$ , bei Eintritt von $E_3$ gibt es nichts, also $0\,€$ . Bei Eintritt von $E_2$ ist der Auszahlungsbetrag unbekannt. Für diesen musst du - und dies ist für die weitere Lösung der Aufgabe entscheidend - einen (unbekannten) Wert $x$ ansetzen.
In Teilaufgabe a) sind die jetzt zu verwendenden Wahrscheinlichkeitswerte für $E_1$ und $E_2$ angegeben: $P(E_1)=P(E_2)=\frac1 6$ . Damit errechnest du $P(E_3)$ : $\frac16 + \frac16 + P(E_3)=1\quad\quad\text{Löse nach }P(E_3) \text{ auf}$ $\quad\quad \quad \;P(E_3)=\frac23$
Die Zufallsgröße $Z:\text{"Auszahlungsbetrag"}$ fasst du in einer Tabelle der Wahrscheinlichkeitsverteilung wie folgt zusammen:
$\def\arraystretch{1.25} \begin{array}{c|c|c|}k&10&x&0\\ \hline P(Z=k)&\frac16&\frac16&\frac23 \end{array}$
Jetzt kommt der Einsatz von $5\,€$ ins Spiel:
Es handelt sich um ein sogenanntes faires Spiel. Dies kommt durch folgende Angabe zum Ausdruck:
"Bei dem Spiel ist zu erwarten, dass die Höhe des im Mittel zu erwartenden Auszahlungsbetrags gleich dem Einsatz pro Spiel ist."
Also muss hier gelten: $\quad E(Z)=5$
Für den Erwartungswert von $Z$ gilt:
$E(Z)=10\cdot\frac16 + x \cdot \frac16 + 0 \cdot \frac{2}{3}$
Setze $E(Z)$ gleich $5$ und löse die Gleichung nach $x$ auf.
$\def\arraystretch{1.25} \begin{array}{rcll}10\cdot \frac16+x\cdot \frac16&=&5&|\cdot 6\\10+x&=&30&|-10\\x&=&20 \end{array}$
Wenn drei verschiedene Farben erscheinen, ist ein Betrag von $20\,€$ auszubezahlen.
Anmerkung zur Aufgabenstellung:
Die Wahrscheinlichkeiten für die Ereignisse "drei gleiche Farben" und "drei verschiedene Farben" sind in Teilaufgabe a) deshalb vorgegeben, damit du - auch wenn du den Aufgabenteil a) nicht schaffst - im Teil b) weiterarbeiten kannst. Ein freundlicher Akt der Aufgabensteller!
Lösung Teilaufgabe c)
So kannst du überlegen:
Die Größe des Mittelpunktswinkels der Sektoren ist direkt proportional zur Wahrscheinlichkeit, den Sektor beim Drehen zu erhalten.
Es sei $p$ die Wahrscheinlichkeit, mit der der grüne Sektor erscheint, also $P(G)=p$ .
Dann gilt gemäß der Aufgabenstellung nach Verkleinerung des grünen und des roten Sektors weiterhin: $P(Rot)=2p$ .
Und für den (restlichen) blauen Sektor ergibt sich:
$P(B)=1-p-2p=1-3p$ .
Dem abgebildeten Baumdiagramm entnimmst du mit der 1. Pfadregel:
$\def\arraystretch{1.25} \begin{array}{rcl}\underbrace{P(R)}_{\color{red}{2p}}\cdot \underbrace{P(B)}_{\color{blue}{1-3p}}&=&\underbrace{P(R\cap B)}_{0{,}14}\end{array}$
Beachte die Unabhängigkeit der aufeinderfolgenden Drehungen ("Ziehen mit Zurücklegen"). Deshalb gilt im Baumdiagramm $P(B|R)=P(B)=1-3b$ .
Jetzt löst du die erhaltene Gleichung für $p$ :
$\def\arraystretch{1.25} \begin{array}{rcll}2p \cdot (1-3p)&=&0{,}14 &|\,\text{ausmultiplizieren}\\2p-6p^2&=&0{,}14 &|\,-0{,}14\\-6p^2+2p-0{,}14&=&0&|\,\text{Mitternachtsformel}\\p_{1{,}2}&=&\displaystyle\frac{-2\pm\sqrt{2^2-3{,}36}}{2\cdot (-6)}\\p_{1{,}2}&=&\displaystyle\frac{-2\pm0{,}8}{-12}\\p_1&=&0{,}1\\p_2&=&\displaystyle\frac{7}{30}\;\color{red}{>}\frac{1}{6}\end{array}$
Da der grüne Sektor verkleinert werden soll, entfällt $p_2$ .
Den Mittelpunktswinkel $\beta$ des (verkleinerten) grünen Sektors berechnest du abschließend so:
$\displaystyle \quad\frac{\beta}{360°}=0{,}1\quad\Rightarrow\quad\beta=36°.$
Die Größe des verkleinerten grünen Sektors beträgt 36°.
Alternative Lösung für Teilaufgabe c)
Die Textvorgabe (Verkleinerung der Sektoren "G" und "R" mit doppelt so großem Mittelpunktswinkel bei "R") ergibt folgende Winkelbeziehung:
$\def\arraystretch{1.25} \begin{array}{rcll}\beta+2\beta+\alpha&=&180°\\\alpha&=&180°-3\beta\end{array}$
$\Rightarrow$ Der Mittelpunktswinkel des (neuen) blauen Sektors beträgt
$180°+\alpha=360°-3\beta$ .
Im Baumdiagramm gilt mit der 1. Pfadregel:
$\def\arraystretch{1.25} \begin{array}{rcll}\displaystyle\frac{2\beta}{360}\cdot \frac{360-3\beta}{360}&=&0{,}14\end{array}$
Berechne den gesuchten neuen Mittelpunktswinkel $\beta$ durch Lösen der Gleichung.
$\def\arraystretch{1.25} \begin{array}{rcll}\displaystyle \frac{2\beta}{360}\cdot \frac{360-3\beta}{360}&=&0{,}14&|\cdot\,360^2\\2\beta\cdot (360-3\beta)&=&18144&|\,\text{Ausmultiplizieren}\\720\beta-6\beta^2&=&18144&|\,\text{als quadratische Gleichung ordnen}\\-6\beta^2+720\beta-18144&=&0&|\,\text{Mitternachtsfomel anwenden}\end{array}$
$\def\arraystretch{1.25} \begin{array}{rcl}\beta_{1;2}&=&\displaystyle \frac{-720 \pm \sqrt{720^2-24\cdot 18144}}{-12}\\\beta_{1;2}&=&\displaystyle \frac{-720\pm 288}{-12}\\\beta _1&=&36\\\beta_2&=&84\end{array}$
Das Ergebnis $\beta=84°$ scheidet aus, da der grüne Sektor (ursprünglich $60°$ ) verkleinert werden soll. Damit ergibt sich auf diesem alternativen Weg die gleiche Lösung eines Mittelpunktswinkel von $36°$ im grünen Sektor des Glücksrades.